大跨度轨道悬索桥合理刚度限值研究
2018-10-18刘安双黎小刚郭向荣
刘安双,黎小刚,,郭向荣,丁 鹏,漆 勇
(1. 林同棪国际工程咨询(中国)有限公司,重庆 401121; 2. 重庆交通大学 土木工程学院,重庆 400074;3. 中南大学 土木工程学院,湖南 长沙 410083)
0 引 言
随着城市规模不断扩大,大跨度轨道交通悬索桥越来越广泛的应用于城市轨道建设中。以主缆为主要承重构件的柔性结构体系[1],轨道悬索桥具有列车荷载激励大、变形明显、抗风能力差等特点,且运营阶段必须满足列车运行安全性和舒适性要求,因此,结构刚度合理取值是设计的控制条件之一。
目前,国内外现有轨道桥梁设计规范中关于桥梁刚度的规定,基本不适用于大跨度轨道悬索桥。在设计大跨度悬索桥时,按照强度要求设计出的桥梁刚度往往难以满足现行规范要求[2],但是,已经存在并安全运营的桥梁可为分析大跨度轨道悬索桥刚度提供参考,因为桥梁安全运营在一定程度上说明了桥梁刚度的合理性[3]。
1 现状分析
1.1 桥梁刚度规定
1.1.1 竖向刚度
桥梁竖向刚度大多采用挠跨比f/L作为评价尺度[4],针对不同桥梁结构类型及车速,有不同的规范限值:
1)日本鉄道構造物等設計標準﹒同解説(変位制限)规定了速度160 km/h和130 km/h的动车、机车以及新干线梁体挠度限值,且对于施加预拱度的桥梁,规定的限值可适当放宽[5]。
2)德国用荷载UIC-71乘以φ(冲击系数)计算竖向变形,最不利变形按考虑扭转时仅单线加载和双线加载两种方法确定。
3)国际铁路联盟(UIC)规定:f/L≤1/800[6]。
4)美国AREA规定:f/L≤1/640[6]。
5)前苏联规定:f/L≤1/(800-1.25L)≤1/600。
6)我国铁路桥涵设计规范规定,梁式桥跨结构在列车竖向静活载作用下的竖向挠度限值位于L/900~L/700[7]。
由此,德国与日本的规范中竖向刚度限值与速度有密切关系,车速越大,刚度要求越严格,其他国家规范没有明确车速与刚度的关系,而针对大跨度轨道悬索桥的竖向刚度,则缺乏明确规定。
1.1.2 横向刚度
基于设计水平荷载的桥梁横向刚度限值,各国规定存在一定差异:
1)国际铁路联盟(UIC)仅对行驶高速列车(120 km/h 2)欧洲铁路结构物荷载标准规定,在列车横向摇摆力、离心力、风力和温度力作用下,简支梁端部的横向角度变化不超过2‰弧度。 3)法国国铁规定,由于列车动力影响而产生的位移量限制在0.4 mm/m以内则使用弦长法[8]。 4)德国规定,由墩台横向水平位移引起相邻结构物轴线间的水平折角在V>160 km/h区段内不得超过1‰,水平折角按不同荷载组合进行计算[9]。 5)前苏联桥梁检定规程对前苏联运行线路上的实测资料进行统计分析,确定:A 6)我国铁路桥涵设计规范从梁体水平挠度和墩台横向位移两个方面,对桥梁横向刚度的限值进行了规定。 1.1.3 梁端折角 桥梁在荷载作用下会产生挠曲,挠曲后主梁梁端处切线与水平方向的夹角即为梁端折角。以竖向梁端折角为例,如图1,θ1和θ2分别为相邻两片梁之间的竖向梁端折角,θ为桥台与桥梁之间的竖向梁端折角。 图1 竖向梁端折角示意 日本新干线网结构物设计标准规定,在列车速度110 km/h以下,双侧竖向梁端折角限值为9.0‰;国际铁路联盟(UIC)规定,单线桥梁竖向梁端折角限值为6.5‰(单侧)和10.0‰(双侧);而针对中低速铁路,我国规范对竖向梁端折角无相应规定。 由此,综合考虑列车走行的安全性和轨道结构的稳定性,大跨度轨道悬索桥双侧竖向梁端折角限值可取9.0‰,单侧可取4.5‰,同理,双侧横向梁端折角限值可取6.0‰,单侧可取3.0‰。 1.1.4 加速度 欧洲规范EUROCODE规定,有砟轨道桥梁竖向加速度限值为3.5 m/s2。我国秦沈客运专线研究和设计中,桥梁竖向加速度限值为3.5 m/s2。 由此,大跨度轨道悬索桥竖向加速度限值可取3.5 m/s2。同理,依据日本国铁技术研究所试验结果、我国铁路桥梁检定规范等,横向加速度限值可取1.4 m/s2。 基于桥位资源珍贵、工程经济等因素综合考虑,在役大跨度轨道悬索桥一般为公路和铁路的合建桥,以日本为例,竖向刚度控制参数见表1。 表1 典型在役公铁两用悬索桥竖向刚度控制参数Table 1 Control parameter of vertical stiffness for typical railwaysuspension bridge in service 对比现有规范与典型在役公铁两用悬索桥可知,相对于中小跨度轨道桥梁,在役大跨度轨道悬索桥刚度偏小,不符合现有规范的刚度限值规定,但目前仍处于正常运营状态。 依据日本鉄道構造物等設計標準﹒同解説(変位制限),梁体通常在水平方向具有比较大的刚性,由于一般伴随车辆运行的变形较小,故没有对水平方向的梁体挠度进行规定。对于认为水平方向刚性小的场合,一般按照将水平方向梁体挠度不超过垂直方向设计极限值的1/2进行设计为宜。因此,在确定大跨度轨道悬索桥竖向刚度限值的基础上,横向刚度限值即可相应确定,考虑安全储备和经济因素,下限可乘上安全系数(取1.2),如竖向刚度限值取1/500,则横向刚度限值为1/1 200。进行横向刚度的验证,应计入列车横向摇摆力、离心力、风力和温度力作用,检算桥跨结构梁体的横向水平挠度,要求满足列车运行安全性和舒适性。其中,风力应依据相关标准规范(如GB/T 51234—2017城市轨道交通桥梁设计规范)执行,当风荷载与列车荷载组合时,按运营风处理。 综合国内外规范中关于轨道桥梁刚度限值的规定、典型在役大跨度轨道悬索桥结构刚度参数控制标准和运营状态、在建轨道桥梁静力特性分析与风-车-桥耦合振动分析列车过桥走行性结果、横向刚度取值与竖向刚度关系,考虑适宜安全储备等因素,针对性提出大跨度轨道悬索桥建议的合理刚度限值范围,如表2和表3。 表2 大跨度轨道悬索桥竖向刚度限值范围建议Table 2 Suggested range of vertical stiffness limit for long-spantrack suspension bridge 表3 大跨度轨道悬索桥横向刚度限值范围建议Table 3 Suggested range of transverse stiffness limit for long-spantrack suspension bridge 针对竖向刚度,依据表2,上限值可取为1/300,结合国内多座正常运营和在建轨道悬索桥的竖向刚度,下限值可取为1/500。以在建重庆鹅公岩轨道专用桥为例,经静力特性分析,在列车竖向静活载和人群荷载作用下,竖向刚度为0.987 m+0.203 m=1.190 m 大跨度轨道悬索桥静力特性分析宜采用杆系有限元方法,主缆以分段悬链线索单元模拟,吊索以索单元模拟,桥塔和主梁以梁单元进行模拟,边界条件按实际情况处理,考虑主力(永久作用或经常作用的荷载,包括恒载和活载)、附加力(不经常发生或发生概率较小的荷载)和特殊荷载(发生概率极小、作用时间短、有的还是灾难性的荷载),按照可能出现的最不利组合情况进行计算[7]。其中,竖向刚度分析时,计入列车竖向静活载作用和人群荷载作用;横向刚度分析时,计入列车横向摇摆力、离心力、风力和温度力作用。 采用车辆桥梁时变系统模型,利用计算程序TBI(Train Bridge Interconnection),建立空间振动分析模型,依据Wilson-θ法,得到车辆结构和桥梁结构的动力响应。 车辆采用两系四轴车,依据多体系统动力学进行计算,将车辆视为运动的多刚体系统,建立空间振动模型,如图2,进行大跨度轨道悬索桥车辆振动分析。分析时采用如下假定: 1)车体、转向架和轮对均为刚体。 2)不考虑车辆、车辆纵向振动和车辆对桥梁振动与行车速度的影响。 3)轮对、转向架和车体均作微振动。 4)弹簧均为线性,阻尼按粘滞阻尼计算,蠕滑力按线性计算。 5)沿铅垂方向,轮对与钢轨的竖向位移相同。 6)忽略构架点头运动、轮对侧滚和摇头运动。 由此,车辆空间振动有侧摆、侧滚、摇头、点头、沉浮5个自由度,每个轮对有侧摆和摇头2个自由度,整个四轴车辆共23个自由度,按二系弹簧计算[12]。 图2 列车空间振动分析模型Fig. 2 Analysis model of spatial vibration of train 根据D’Alembert原理,建立车辆运动方程[13] (1) 利用有限元计算程序,采用索单元、梁单元等,设置符合实际的边界条件,建立精细化模型。由动力学势能驻值原理及形成矩阵的“对号入座”法则[14],建立桥梁质量、阻尼和刚度矩阵,进而得到桥梁的运动方程: (2) 车辆与桥梁相互作用关系体现在轮轨接触处几何位移关系和轮轨相互作用力[15],即未发生脱轨情况下,在轮轨接触处,列车和桥梁具有相同位移协调条件,所受荷载为大小相等、方向相反的作用力。 联立公式(1)和公式(2)即得车辆与桥梁相互作用模型,进行分别独立求解车辆和桥梁运动方程,再通过分离迭代[16-17],以满足车辆与桥梁相互作用关系。 轨道不平顺包括轨道垂向、方向、水平和轨距的不平顺。作为大跨度轨道悬索桥,轨道不平顺可视为沿轨道全长近似平稳的随机过程,采用美国六级线路谱,模型建立如下: 1)垂向不平顺: (3) 2)方向不平顺: (4) 3)水平和轨距不平顺: (5) 式中:S(Ω)为轨道不平顺功率谱密度;Ω为空间频率;Ωc,Ωs为截断频率;Av,Aa为粗糙度系数;K=0.25。 重庆鹅公岩轨道专用桥为自锚式悬索桥,主桥跨径组合为50 m+210 m+600 m+210 m+50 m,结构布置如图3;主梁采用钢箱梁形式,梁高4.5 m,梁宽22.0 m,横截面布置如图4;桥塔采用门式框架结构,塔柱为钢筋混凝土,混凝土等级为C50;主缆中跨矢跨比为1/10,共设两根主缆,由91股钢丝束组成,直径为625 mm;吊杆共122根,标准强度为1 770 MPa,间距为15 m。 图3 桥梁结构布置(单位:cm)Fig. 3 Layout of bridge structure f 图4 横截面布置(单位:cm)Fig. 4 Layout of cross section 进行风-车-桥耦合振动分析,设计行车速度为80 km/h,检算按100 km/h计,列车编组和计算工况见表4。 表4 列车编组和分析工况Table 4 Train group and analysis condition 参照国内外规范关于列车走行性规定,借鉴铁路桥梁风-车-桥耦合振动分析评价实例,车辆评价标准见表5,桥梁评价标准按表2和表3执行。 表5 车辆评价指标限值Table 5 Limit of vehicle evaluation index 鹅公岩轨道专用桥静力特性计算采用空间非线性分析软件TDV RM Bridge,根据桥梁实际结构进行空间杆系离散,塔底与墩底均固结,主缆在主梁锚固点固结,主梁在顺桥向无约束,竖桥向和横桥向在桥墩与桥塔处被约束,结构空间单元离散见图5。 图5 桥梁有限元模型Fig. 5 Bridge finite element model 经分析,鹅公岩轨道专用桥在列车竖向静活载和人群荷载作用下,竖向位移包络分别如图6、图7,竖向刚度0.987 m+0.203 m=1.190 m 图6 列车荷载作用下竖向位移包络图(单位:m)Fig. 6 Envelope of vertical displacement under the train load 图7 人群荷载作用下竖向位移包络图(单位:m)Fig. 7 Envelope of vertical displacement under the crowd load 经风-车-桥耦合振动分析,得到桥梁动力响应、列车运行安全性和舒适性指标的最大值,并与评价标准进行对比分析,结果见表6和表7。其中,振动位移评价经挠跨比限定标准换算,并扣除人群荷载作用。 表6 桥梁动力响应计算最大值与分析评价Table 6 Maximum value of bridge dynamic response and analysis evaluation 表7 车辆响应计算最大值与分析评价Table 7 Maximum value of vehicle dynamic response and analysis evaluation (续表7) 工况风速/(m·s-1)车速/(km·h-1)脱轨系数Q计算评价轮重减载率ΔP计算评价轮对横向力/kN计算评价加速度/(m·s-2)竖向横向计算评价计算评价Sperling舒适性指标竖向横向计算评价计算评价双线015202560~800.26满足0.29满足13.67满足0.77满足0.53满足2.45优秀2.52良好90~1000.40满足0.43满足16.86满足0.91满足0.71满足2.58良好2.60良好60~800.28满足0.32满足15.26满足0.85满足0.72满足2.54良好2.55良好90~1000.47满足0.48满足18.91满足1.05满足0.85满足2.63良好2.64良好60~800.36满足0.34满足18.36满足0.93满足0.73满足2.59良好2.58良好90~1000.54满足0.50满足21.70满足1.14满足0.94满足2.72良好2.72良好60~800.47满足0.38满足22.91满足1.11满足0.90满足2.62良好2.64良好90~1000.67满足0.57满足29.77满足1.21满足0.96满足2.78合格2.76合格 综上,依据静力特性分析结果,鹅公岩轨道专用桥竖向刚度、竖向梁端折角、横向刚度、横向梁端折角等均满足刚度限值建议;依据风-车-桥耦合振动分析评价结果,单线或双线A型车以60~100 km/h通过桥梁时,桥梁动力响应正常,列车运行安全性满足要求,车体横向和竖向振动加速度满足限值规定,舒适性达到“合格”标准,桥梁和车辆可正常运营。故鹅公岩轨道专用桥设计采用的竖向刚度和横向刚度合理。 1)经静力特性分析和风-车-桥耦合振动分析,重庆鹅公岩轨道专用桥结构静力特性、动力响应和列车走行性均满足要求,说明设计的结构型式得体,刚度适宜,验证了大跨度轨道悬索桥刚度限值范围建议的合理性。 2)依据现有国内外规范关于桥梁刚度的规定,经在役大跨度悬索桥刚度设置和运营状态的广泛调研与总结,提出大跨度轨道悬索桥合理刚度限值建议,并采用杆系有限元方法和风-车-桥耦合振动分析方法,应用工程实例,验证了刚度限值的合理性,对同类工程设计具有重要借鉴意义,但修订和完善规范相关规定,则需进一步检验。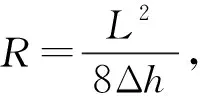

Fig. 1 Diagram of vertical beam-end rotation angle1.2 在役大跨度轨道悬索桥
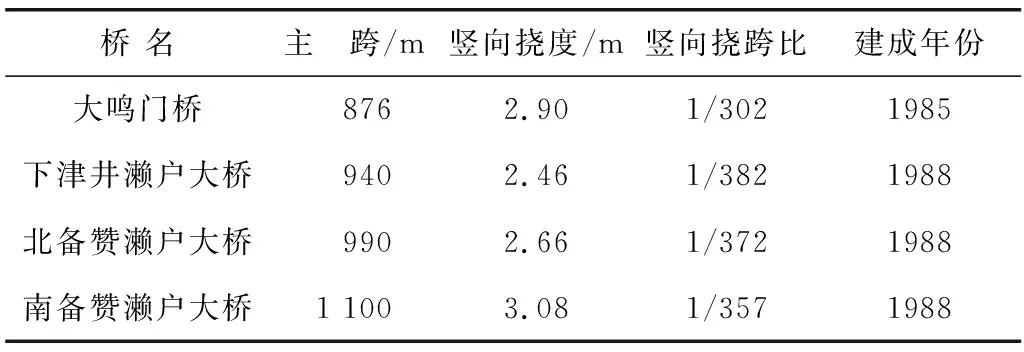
1.3 横向刚度取值
2 合理刚度限值建议


3 静力特性分析
4 风-车-桥耦合振动分析
4.1 车辆模型

4.2 桥梁模型

4.3 车辆与桥梁相互作用模型
4.4 轨道不平顺模拟
5 工程实例
5.1 桥梁概况
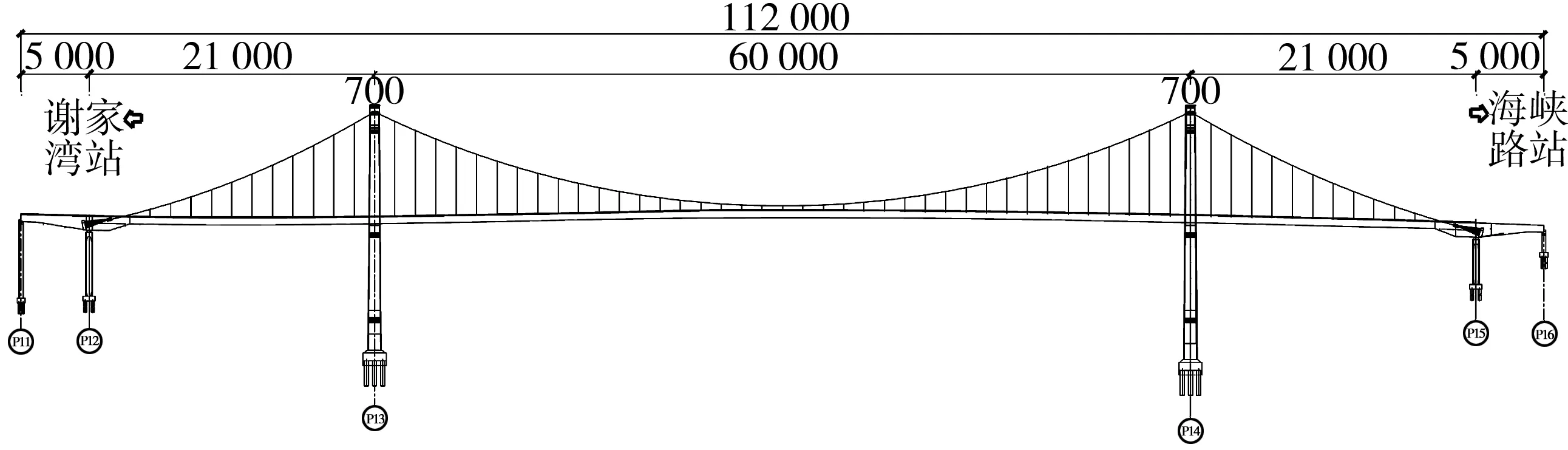

5.2 列车编组和分析工况

5.3 评价标准

5.4 静力特性分析结果



5.5 风-车-桥耦合振动分析结果
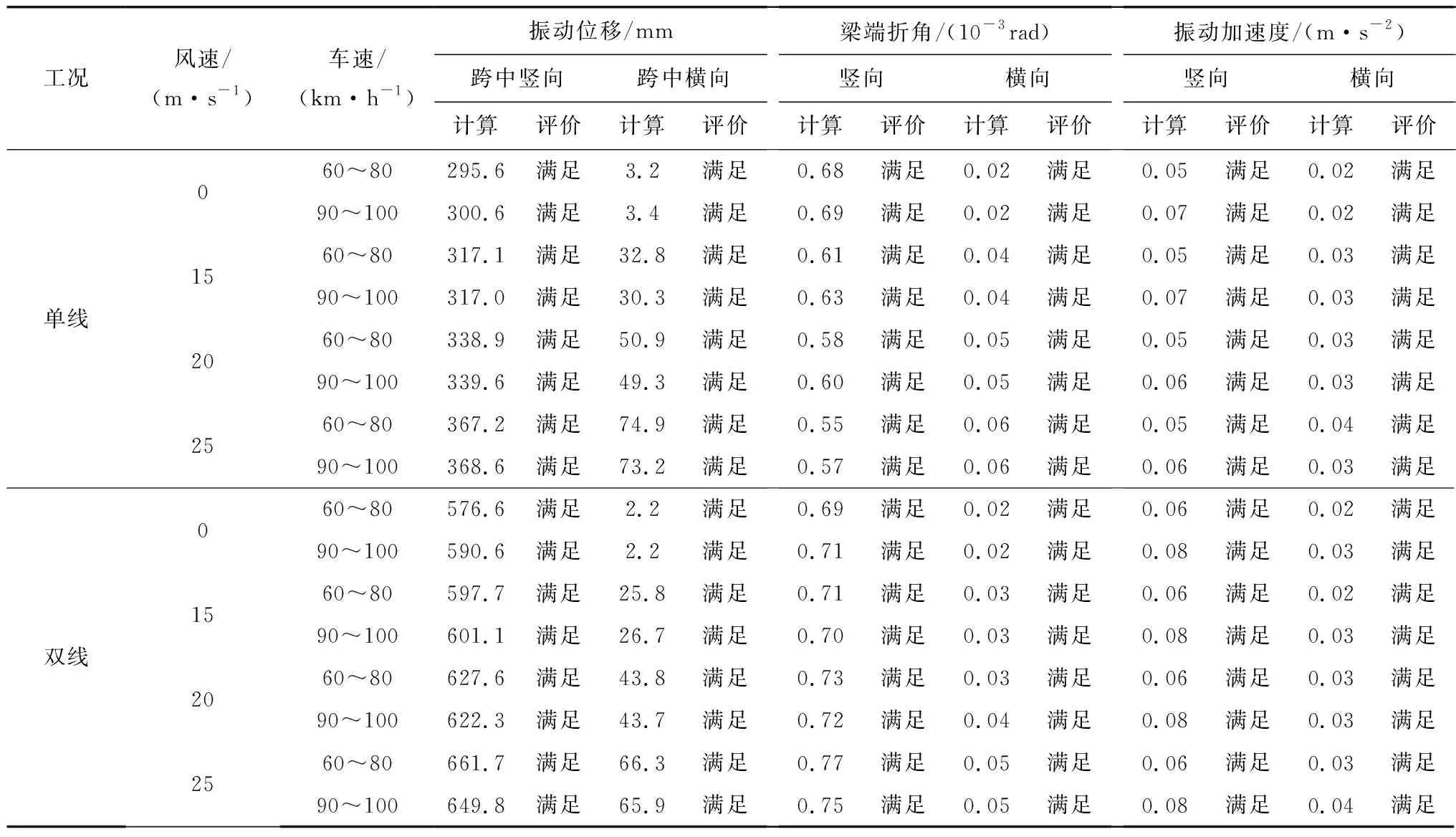


6 结 语
