基于双强度折减法的顺层岩质边坡稳定性分析
2018-10-18郭建军
郭 建 军
(1. 重庆交通大学 河海学院,重庆400074; 2. 重庆水利电力职业技术学院 建筑工程学院,重庆402160)
0 引 言
边坡失稳破坏是一个累积性的变化过程,该变化过程中伴随着岩土体参数的弱化。在这个累积性变化过程中,抗剪强度参数黏聚力和内摩擦角是主要的影响因素,自O. C. ZIENKIEWICZ等[1]、K. A. UGAI[2]提出强度折减法以来,强度折减法得到了国内外广泛的研究[3-5]。
边坡稳定性计算分析中黏聚力和内摩擦角对其影响机制是不同的,在折减过程中也是有差异性的。洪毓康[6]认为,未加固的滑动面上的阻抗力由黏聚力和摩阻力两部分组成,边坡发生滑动时,滑动面上摩阻力首先得到充分发挥,然后才有黏聚力作补充。赵炼恒、郑颖人、唐芬等[7-11]在条分法的基础上推导了双安全系数的隐式关系,说明了对采用非等比例折减的合理性。薛海斌等[12]对边坡强度参数等非等比例关联法进行了研究,针对土体的抗剪强度峰值和残余强度关系建立了双参数折减法的比例关系。袁维等[13-15]根据c-tanφ的临界曲线关系,定义了边坡整体安全系数的定义方法。对于岩质边坡,其稳定性受到滑面物理力学参数和潜在滑动面的位置影响,其内摩擦角和黏聚力对坡体稳定性的影响程度就不同。如果采用等比例强度折减法,势必会对坡体的稳定性计算造成误差。对于如何选择适合的折减系数,如何确定两个折减系数之间的关系,以及如何定义边坡的整体安全系数是个亟待解决的问题[16]。
笔者以极限平衡法理论为基础,对顺层岩质边坡进行强度折减分析,分别以坡体的张拉裂缝深度和充水深度为单一变量,对比分析边坡稳定性发生变化时内摩擦角和黏聚力对其影响程度,最后根据双强度折减分析结果定义坡体安全系数。
1 双强度折减法的提出
抗剪强度参数是影响边坡稳定性最主要的因素,而含水率变化对抗剪强度参数影响很大。
岩土材料是双强度材料,试验表明:当水平位移很小时,抗剪强度迅速增加,黏聚力发挥作用,随着水平位移的增大,内摩擦角逐渐发挥作用并随之增大,直至达到极限值;在边坡发生滑动时,黏聚力首先得到充分发挥,随着应变增加,内摩擦角才逐渐发挥作用[6]。
双强度折减法的基本原则:折减后的双强度参数应符合边坡失稳的实际强度特征。在边坡的稳定性分析中,采用双折减系数能更准确地反映c、φ对边坡的影响程度,也就具有了重要的理论意义和工程实用价值[11]。因此,定义抗剪强度参数折减系数SRF(shear reduction factor)即
(1)
式中:SRFφ为内摩擦角φ的折减系数;SRFc为黏聚力c的折减系数;φ1、c1分别为折减后土体的内摩擦角和黏聚力。
2 双强度折减法综合分析
岩土体的抗剪强度参数c、φ值在坡体稳定性分析中发挥着不同的作用,其对坡体稳定性的影响程度是有差异的,如何合理地考虑其影响程度来进行坡体稳定性分析是笔者将要研究的内容。
1)当黏聚力单一折减
当滑移面的内摩擦角不发生改变,黏聚力逐渐减小,直至坡体达到极限平衡状态时,即抗滑力等于下滑力时,得到极限黏聚力值。
2)当内摩擦角单一折减
当滑移面的黏聚力不发生改变,内摩擦角逐渐减小,直至坡体达到极限平衡状态时,即抗滑力等于下滑力时,得到极限内摩擦角值。
3)双强度折减综合分析
分别对内摩擦角和黏聚力进行单一折减后,得到极限内摩擦角和黏聚力,可以得到它们对坡体稳定性的影响程度。在此按照抗剪强度折减系数增幅值引入折减系数比值q:
(2)
再根据抗剪强度折减系数增幅比值q,对边坡进行双参数综合折减分析,最后根据内摩擦角和黏聚力的权重关系确定边坡安全系数。图1为双强度折减法的流程。
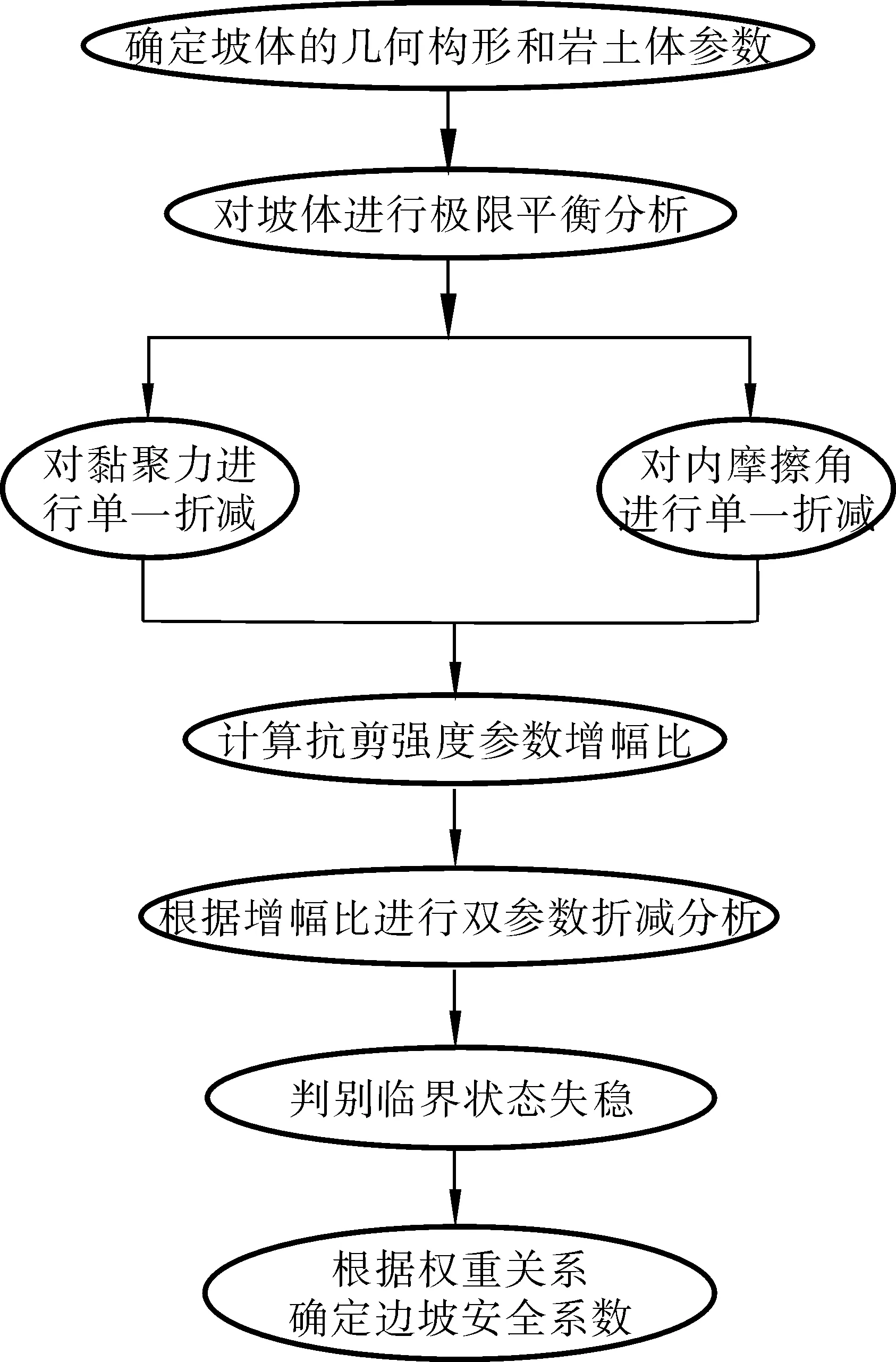
图1 双强度折减法分析流程Fig. 1 Analysis flow chat of double strength reduction method
3 顺层岩质边坡极限平衡法分析
顺层岩质边坡中,结构面往往控制着坡体的稳定性,坡体失稳通常会产生张拉裂缝。如果滑移面的走向与自然坡面的走向大体相同,根据坡体的几何结构和地下水状况,顺层岩质边坡从坡趾破坏,张拉裂缝的产生会有两种情况:①张拉裂缝在上部坡面;②张拉裂缝在自然坡面。图2为不同坡体结构的张拉裂缝位置分析。
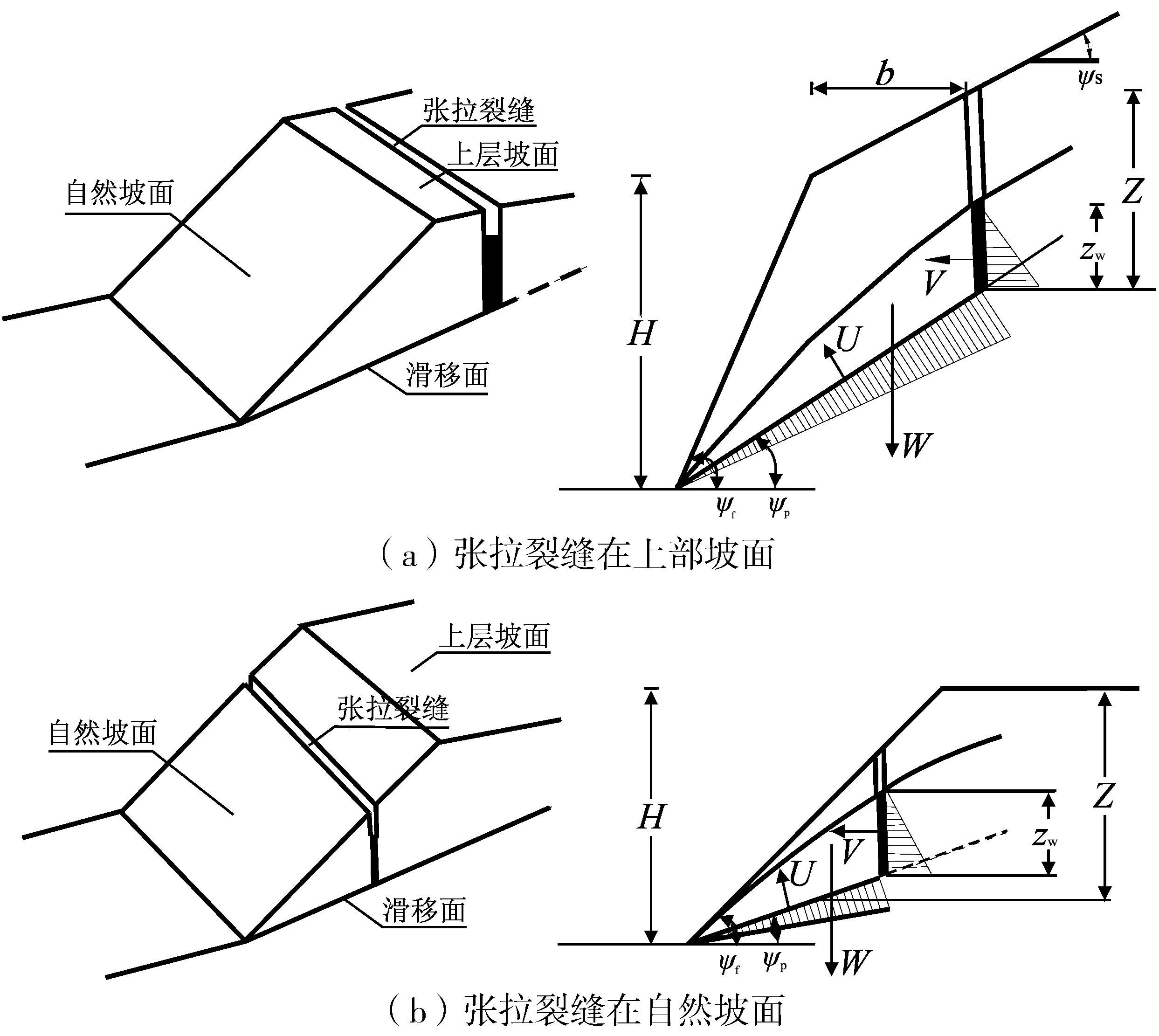
图2 不同坡体结构的张拉裂缝位置分析Fig. 2 Analysis of the tension crack location of different slopestructures
根据E. HOEK等[17]提出的顺层岩质边坡极限平衡法,滑移块体的安全系数为抗滑力与下滑力之比,其计算式为
(3)
式中:c为滑移面的黏聚力;φ为滑移面的内摩擦角;A为滑移面的面积。
若滑面上的黏聚力和内摩擦角对坡体的稳定性影响程度不同,利用强度折减法对其进行分析,将滑面上的黏聚力和内摩擦角进行折减,但两者的折减系数不同,假定滑移体可达到极限平衡,即滑面上的抗滑力等于下滑力,则
(4)
式中:SRFφ为内摩擦角φ的折减系数;SRFc为黏聚力c的折减系数。
假定滑移块体处于极限平衡状态,则
∑N=Wcosψp-U-Vsinψp
(5)
∑S=Wsinψp+Vcosψp
(6)
(7)
式中:H为坡高;z为张拉裂缝的深度;b为张拉裂缝距坡顶的水平距离;ψs为上部坡面的倾角;ψp为滑移面的倾角,其物理参数意义如图2。
当张拉裂缝中的充水深度为zw时,滑移面上的水压U和张拉裂缝上的水压V为
(8)
(9)
式中:γw为水的容重。
根据图2(a)中,当张拉裂缝在上部坡面时,滑移块体的重量为
(10)
在图2(b)中,当张拉裂缝位于自然坡面时,滑移块体的重量为
(11)
式中:γr为岩体容重;ψf为自然坡面的坡角。
4 案例分析
笔者选取某岩质坡体进行计算,现对不同折减系数下的顺层岩质边坡稳定性进行分析,坡体算例的几何构型和参数如下:坡高H=20 m,岩体容重γr=20 kN/m3,水的容重γw=10 kN/m3。根据相关现场试验和经验对滑移面的物理力学参数进行取值,滑移面的黏聚力c=20 kPa,内摩擦角φ=30°。
4.1 张拉裂缝位置变化
4.1.1 当张拉裂缝在上部坡面时
当张拉裂缝在上部坡面时,假定上部坡面的倾角ψs为30°,自然坡面的倾角为45°,张拉裂缝深度为10 m,充水深度为3 m,张拉裂缝距坡顶的距离为5 m,则滑移面的倾角为27.27°。
1)黏聚力单一折减
当滑移面的内摩擦角不发生改变,黏聚力逐渐减小时,直至坡体达到极限平衡状态,即抗滑力等于下滑力,表1为计算结果。
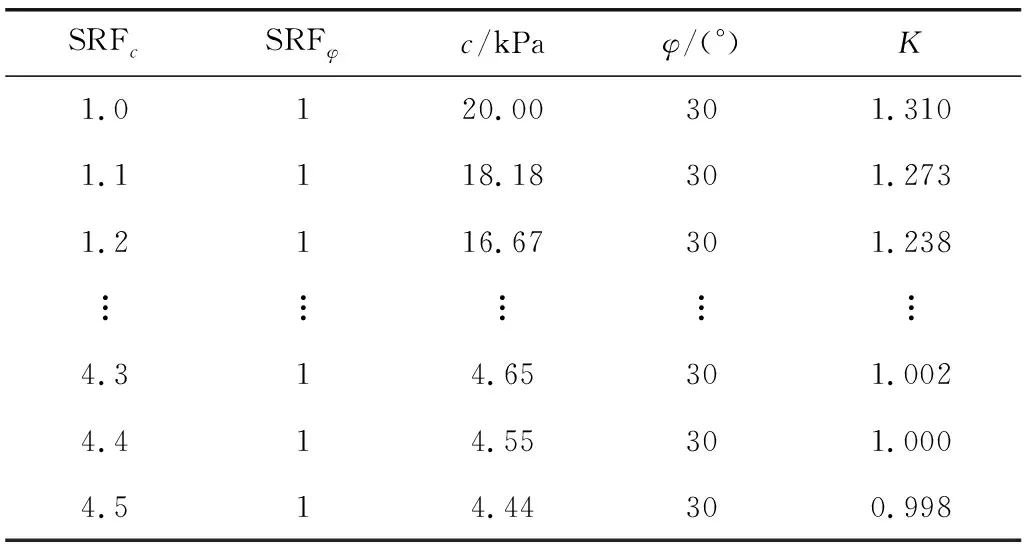
表1 黏聚力单一折减Table 1 Cohesion single reduction
从表1中计算结果分析得到,当黏聚力的单一折减系数为4.4时,即黏聚力为4.55 kPa时,K为1,坡体将达到极限平衡状态。
2)内摩擦角单一折减
当滑移面的黏聚力不发生改变,内摩擦角逐渐减小时,直至坡体达到极限平衡状态,即抗滑力等于下滑力,表2为计算结果。从表2中计算结果分析得到,当内摩擦角的单一折减系数为1.5时,即内摩擦角为21.05°,此时K为1,坡体将达到极限平衡状态。
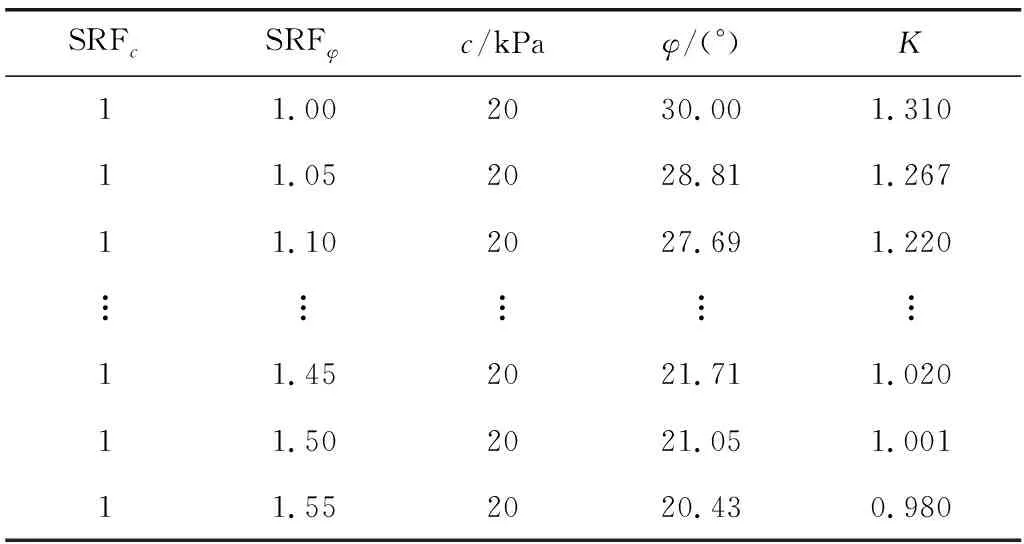
表2 内摩擦角单一折减Table 2 Internal friction angle single reduction
3)双强度折减综合分析
在以上的计算分析中,当内摩擦角参数保持不变,黏聚力的折减系数SRFc=4.4时,黏聚力的增幅为340%,此时边坡的临界高度等于边坡高度;当黏聚力参数保持不变,内摩擦角的折减系数SRFφ=1.5时,内摩擦角的增幅为50%,此时边坡的临界高度等于边坡高度。
参照式(2)计算得到此模型的抗剪强度参数折减系数增幅比q为0.147,下面按照抗剪强度参数折减系数增幅比值q,对该边坡进行双参数综合折减分析,表3为综合分析结果。
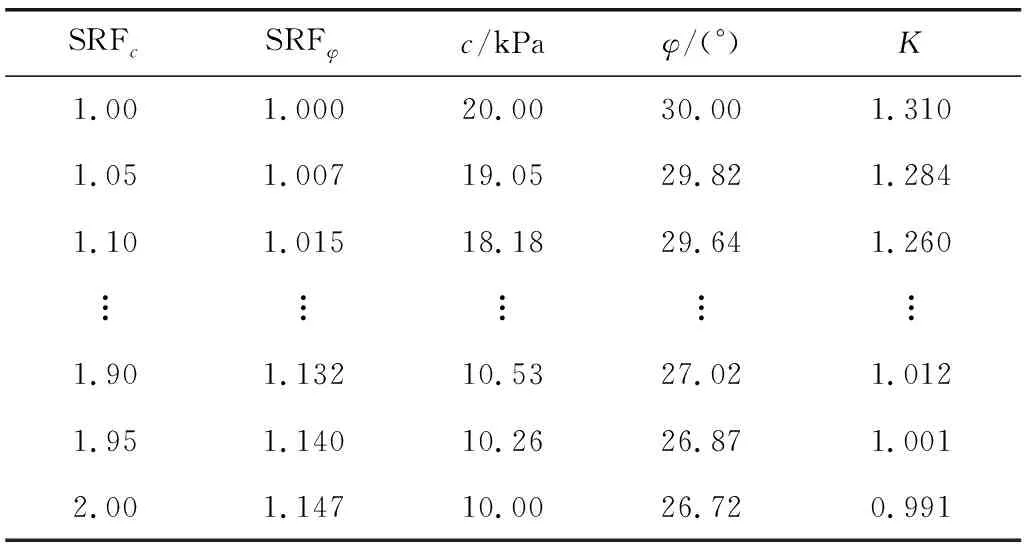
表3 双参数折减综合分析Table 3 Comprehensive analysis of double parameter reduction
根据表3中的计算结果可知,当黏聚力的折减系数为1.95,内摩擦角的折减系数为1.14时,即c=10.26 kPa、φ=26.87°时,坡体达到极限平衡状态。
4.1.2 当张拉裂缝在自然坡面时
当张拉裂缝在上部坡面时,假定上部坡面的倾角ψs为30°,自然坡面的倾角ψf为45°,裂缝深度为7 m,充水深度为3 m,张拉裂缝距坡顶的距离为5 m,则滑移面的倾角为28.07°。
当张拉裂缝位于自然坡面时,双强度折减分析过程和前述相同。
1)黏聚力单一折减
当滑移面的内摩擦角不发生改变,黏聚力逐渐减小,直至坡体达到极限平衡状态,即抗滑力等于下滑力,计算结果分析得到,当黏聚力的单一折减系数为2.85时,即黏聚力为7.02 kPa,此时K为1,坡体将达到极限平衡状态。
2)内摩擦角单一折减
对内摩擦角进行单一折减,计算结果分析得到,当内摩擦角的单一折减系数为1.65时,即内摩擦角为19.29°,此时K为1,坡体将达到极限平衡状态。
3)双强度折减综合分析
按照式(2)所提出的抗剪强度参数增幅比值q,对该边坡进行双参数综合折减分析,计算得到抗剪强度参数增幅比值q为0.351。按照此值进行双强度折减分析,当黏聚力的折减系数为2.05,内摩擦角的折减系数为1.091时,即c=9.756 kPa、φ=27.88°时,坡体达到极限平衡状态。
4.2 张拉裂缝深度变化
当坡体几何构型不发生改变,张拉裂缝距坡顶的距离一定时,随着张拉裂缝的深度发生变化,其坡体滑移面的倾角也将发生改变。图3为张拉裂缝的几何构型分析。
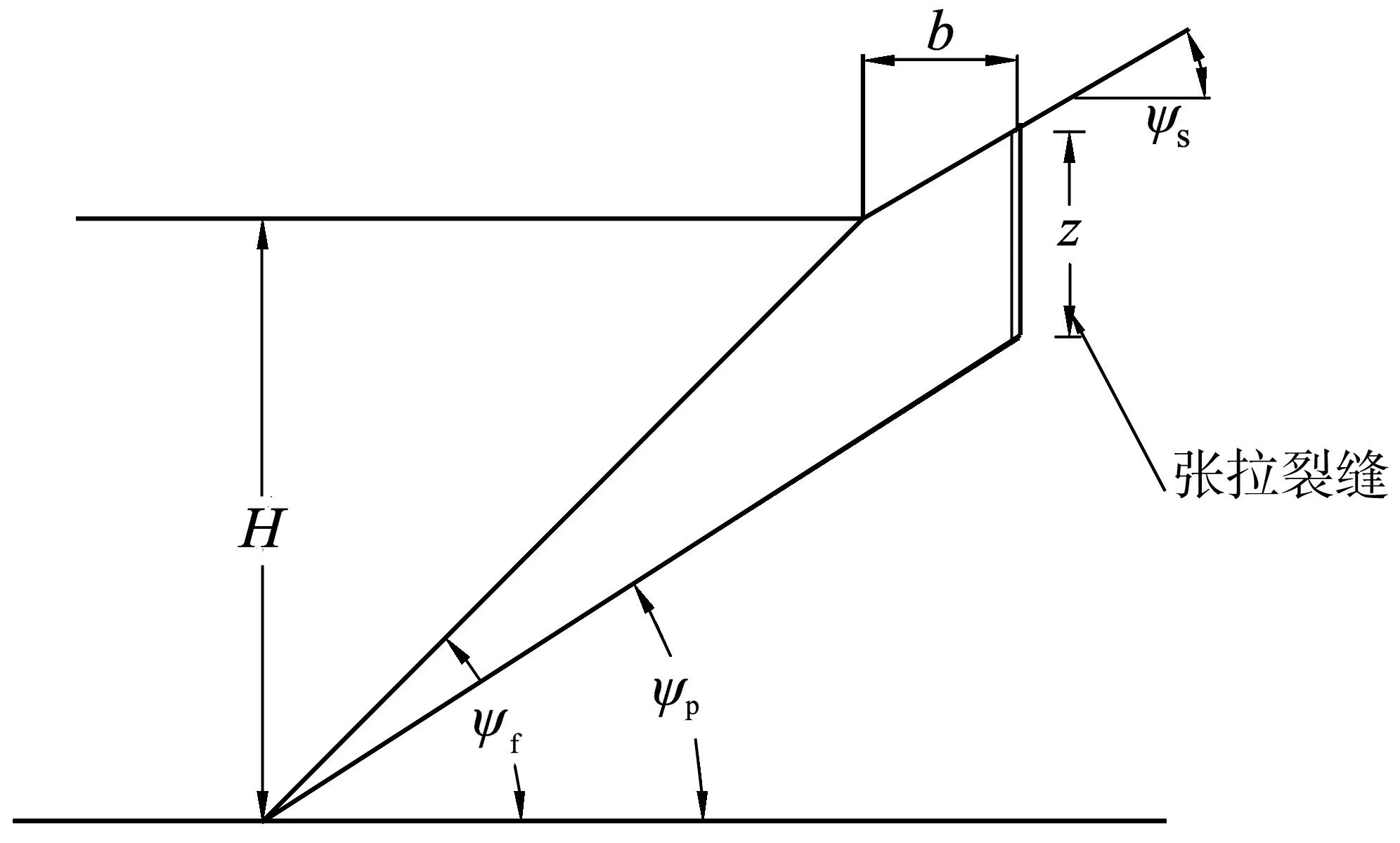
图3 张拉裂缝几何构型分析Fig. 3 Geometric configuration analysis of tension crack
在图3中,随着张拉裂缝的深度发生变化时,滑移面的倾角也将随之发生变化,其几何关系表达式为
(12)
代入相关数据,即:H=20 m,b=5 m,ψs=30°,ψf=45°。
得到张拉裂缝的深度与滑移面倾角的关系为
(13)
改变张拉裂缝的深度,即图3中z,如图2,利用双强度折减综合分析法,分析抗剪强度增幅比和双强度参数折减系数随张拉裂缝深度改变的规律。即先对内摩擦角和黏聚力进行单一折减,根据抗剪强度增幅比再进行双强度折减,求解坡体处于极限平衡状态下的内摩擦角和黏聚力的折减系数。计算结果见表4。图4为双强度折减分析。根据表4和图4中结果可知,通过改变裂缝深度,当张拉裂缝的深度逐渐变大时,此时K值逐渐增大,坡体稳定性增强。在坡体稳定性逐渐提高的过程中,双强度折减法综合分析的抗剪强度增幅比q值逐渐减小,内摩擦角折减系数变化幅度逐渐减小,而黏聚力折减系数变化幅度逐渐变大。
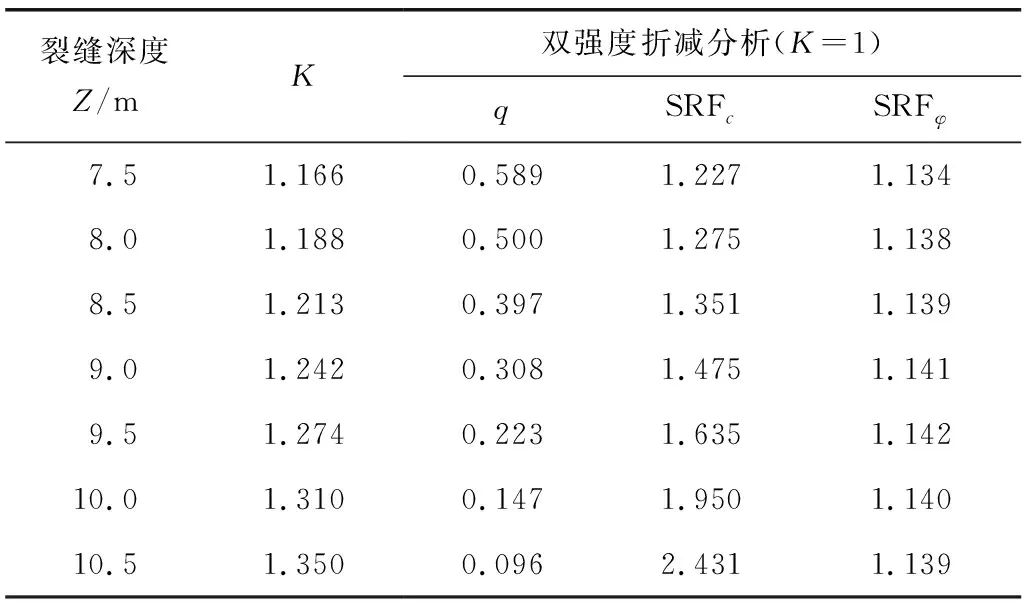
表4 张拉裂缝深度变化时双强度折减分析Table 4 Double strength reduction analysis when the depth of tensioncrack changes
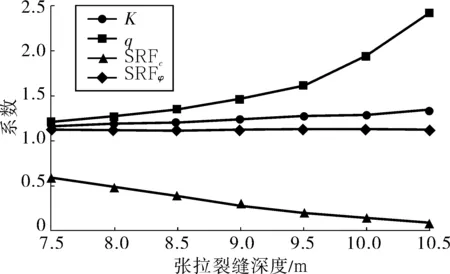
图4 张拉裂缝深度变化时双强度折减分析Fig. 4 Double strength reduction analysis whenthe depth of tension crack changes
4.3 充水深度变化
利用双强度折减综合分析法,通过改变张拉裂缝的充水深度zw,如图2,分析抗剪强度增幅比和双强度参数折减系数随充水深度变化的规律。即先对内摩擦角和黏聚力进行单一折减,根据抗剪强度增幅比再进行双强度折减,求解坡体极限平衡状态下的内摩擦角和黏聚力的折减系数。计算结果见表5。图5为充水深度变化时双强度折减分析。
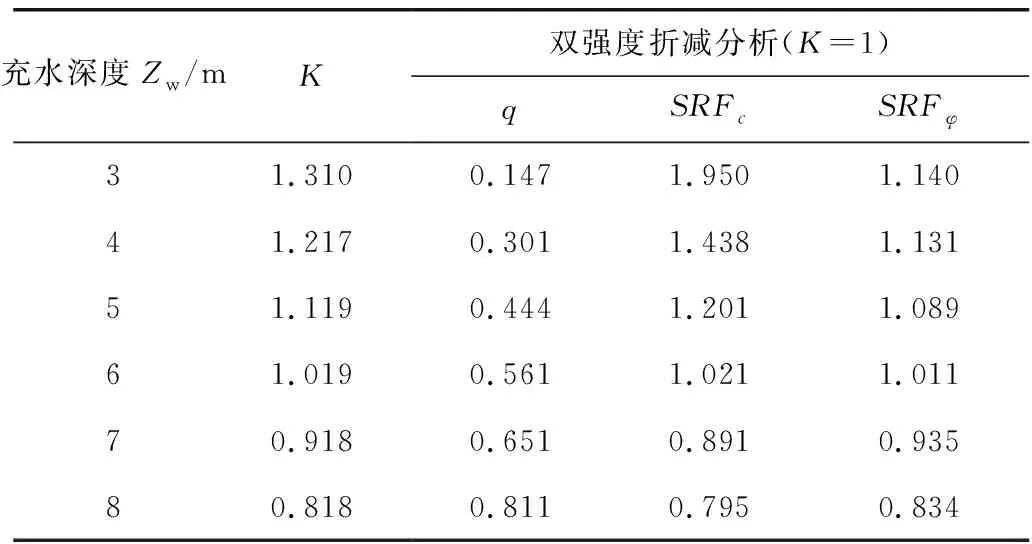
表5 充水深度变化时双强度折减分析Table 5 Double strength reduction analysis when the depth of waterfilling changes
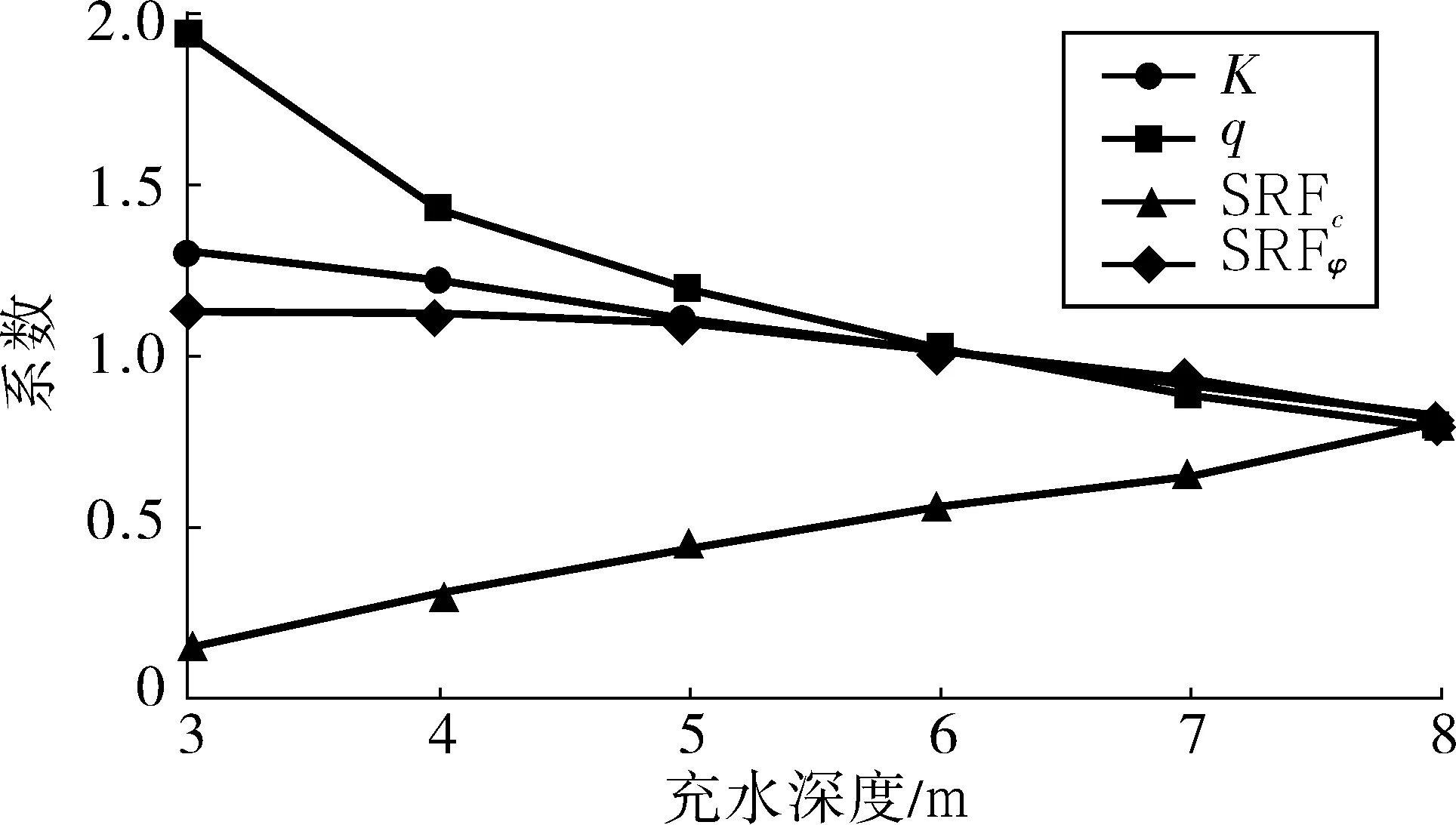
图5 充水深度变化时双强度折减分析Fig. 5 Double strength reduction analysis when the depth of waterfilling changes
根据表5中结果可知,通过改变充水深度,当充水深度逐渐变大时,K值逐渐减小,坡体的稳定性逐渐降低,当充水深度为6 m时,坡体将要达到极限平衡状态。在坡体逐渐失稳的过程中,双强度折减法综合分析的抗剪强度增幅比q值逐渐变大,内摩擦角折减系数变化幅度逐渐变大,而黏聚力折减系数变化幅度逐渐减小,表明内摩擦角对坡体的稳定性影响程度增大,黏聚力对坡体稳定性的影响程度减小。
5 安全系数定义
在上述分别以坡体张拉裂缝深度和充水深度为单一变量时,对坡体进行双强度折减综合分析。
当以张拉裂缝的深度为单一变量时,随着坡体张拉裂缝深度的增加,坡体的抗滑力与下滑力的比值逐渐变大,坡体稳定性逐渐增加,此时坡体处于稳定状态,但是黏聚力折减系数的变化幅度很大,而内摩擦角折减系数几乎没有变化。
当以充水深度为单一变量时,随着充水深度的增加,坡体的抗滑力与下滑力比值逐渐减小,坡体逐渐失稳,此时双强度折减法综合分析的抗剪强度增幅比q值逐渐变大,内摩擦角折减系数变化幅度逐渐变大,而黏聚力折减系数变化幅度逐渐减小,即内摩擦角对坡体的稳定性影响程度增大,黏聚力对坡体稳定性的影响程度减小。
该结论与众多剪切试验结果相同,即当水平位移很小时,抗剪强度迅速增加,黏聚力发挥作用,随着水平位移的增大,摩阻力逐渐发挥作用并随之增大,直至达到极限值;在边坡发生滑动时,滑动面上黏聚力首先得到充分发挥,然后摩阻力得到发挥并达到极限值[6]。
因此应该根据权重指数来定义安全系数的求解,而综合分析法正是根据影响程度进行双参数折减分析,笔者定义安全系数应该为双参数折减结果中内摩擦角的折减系数值为坡体的安全系数,在此并不是只考虑了内摩擦角,而不考虑黏聚力,只是将黏聚力的折减系数纳入了抗剪强度折减系数增幅比中。在坡体的稳定分析中,应更加注意可能失稳状态,即应该侧重于内摩擦角发挥作用的阶段。
6 结 语
利用极限平衡法,对岩质边坡进行稳定性评价分析,确定边坡的极限平衡状态。通过双强度折减法对坡体进行分析,首先对抗剪强度参数中的内摩擦角和黏聚力进行单一折减,确定边坡的极限状态,提出了抗剪强度参数折减系数增幅比,根据其比值确定双折减系数综合分析过程中两者的折减系数,将其折减到一定程度后使得边坡达到极限状态,此时的折减系数值即为极限值。
分别以裂缝所在的位置、裂缝深度和充水深度为单一变量,对比分析坡体的稳定性,利用抗剪强度参数折减系数增幅比,分析内摩擦角和黏聚力对坡体稳定性的影响程度。计算结果表明,当坡体稳定性逐渐降低,抗剪强度迅速增加,黏聚力发挥作用,随着坡体即将失稳,摩阻力逐渐发挥作用并随之增大,直至达到极限值。在边坡发生滑动时,滑动面上黏聚力首先得到充分发挥,然后摩阻力得到发挥并达到极限值。
