机电装备性能退化建模与健康状态评估方法
2018-10-18王远航陶志奎
邓 超,王远航,吴 军,夏 爽,陶志奎
(1.华中科技大学机械科学与工程学院,湖北 武汉 43007;2.工业和信息化部电子第五研究所,广东 广州 510610)
0 引言
高可靠性、长寿命机电装备在航空航天和军工等领域被广泛应用,这些装备的结构功能复杂、生产样本少、退化状况多变、故障模式多样等。随着使用时间的增加,机电装备的一些性能会发生退化,而其退化程度与其寿命必定存在一定的联系,故根据装备的退化数据可以预测出装备的健康状态和剩余寿命。
基于退化数据的可靠性分析在航空航天领域使用较为广泛,文献[1-2]使用多个退化特征量和寿命之间的关系来预估设备在各个时间的可靠度。李伟[3]建立了多个参数融合的航空发动机退化失效模型,并进行了可靠性分析。Yang等[4]根据多性能参数退化的相关性分析,建立了具有独立和非独立的多性能参数的存储可靠性模型,实现了以多性能参数退化为基础的构件存储可靠性评估。一般常用的方法是运用随机分布对性能退化数据进行拟合,其中维纳过程因其良好的分析计算能力,在性能退化建模方面具有显著的优势。文献[5-7]运用维纳过程的模型参数,设计了基于逆高斯过程的性能退化建模与剩余寿命预测方法。但维纳过程建模多用于单性能退化建模。
另外,机电装备健康状态评估采用多种综合评价方法对健康状况进行评估。常用的健康状态评估方法有模型法、模糊评价法、层次分析法(Analytic Hierarchy Process, AHP)、逼近理想解法(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)、贝叶斯网络方法、灰色理论、证据理论等[8-11]。但是其中,AHP和模糊理论主观性和经验性比较强,权重值、模糊规则及隶属函数等很难确定;贝叶斯网络方法、灰色理论、证据理论评估方法也比较复杂。本文以机电装备作为研究对象,建立基于融合维纳过程的多性能退化模型,并根据该模型提出基于逼近理想解法的健康状态评估方法。
1 基于维纳过程的性能退化建模
1.1 维纳过程退化建模方法
维纳过程来源于Brown在研究悬浮微粒在液体中作无规则运动时提出的布朗运动,即漂移参数为0的一元维纳过程。在高倍显微镜下,液体其实是由许许多多分子组成的,液体分子不间断地做无规律的运动,不断地与悬浮微粒随机撞击,由此产生位移,由中心极限定理可把液体分子的运动位移看作一个正态分布。同理,装备在一段时间内的性能退化量是很多随机的同分布的微小性能退化量之和,并且这些微小退化量的数目与时间成正比,则可以说退化量是服从正态分布的[12]。
假设有n个样品,初始时刻性能退化量都为0。在时刻t1至tm对样本性能退化量进行m次测量,得到测量值:
记Δxij=X(tij)-X(ti(j-1)),Δxij为样本i在时刻ti(j-1)和tij之间的性能退化量。根据维纳过程性质可知Δxij~N(μΔtij,σ2Δtij),其中Δtij=tij-ti(j-1),i=1,2,…,n,j=1,2,…,m,则可以推出似然函数为:
(1)
根据式(1)求参数μ,σ2的极大似然估计得:
(2)
1.2 多性能融合维纳过程退化建模
目前针对性能退化建模的研究大都根据单性能退化数据来建立,当该性能参数退化量超过某一阈值,则产品或装备失去指定的功能,即失效。但是实际上产品或装备的性能可由多个性能参数描述,并且这些性能参数都可能随时间的推移和装备的运行而发生退化,这些性能的退化程度有所不同,退化机理也有所不同,但多个性能参数之间可能存在独立或相关的联系,如果将这种联系纳入退化模型,会使退化模型更加精确而有效。设有n个产品的p个性能服从维纳过程,在t时刻性能退化量为(X1(t)X2(t) …Xp(t))′,并且X1(0)=X2(0)=…=Xp(0)=0,这些性能参数的性能阈值为l1,l2,…,lp。则多性能融合维纳过程退化建模的过程如下:
步骤1考虑多个性能参数之间是否相关。两个性能参数之间的关系可以用随机变量相关性系数公式来描述:
(3)
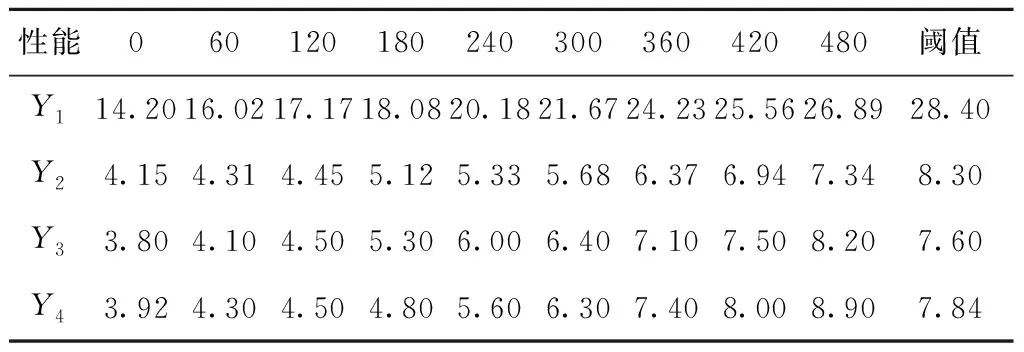
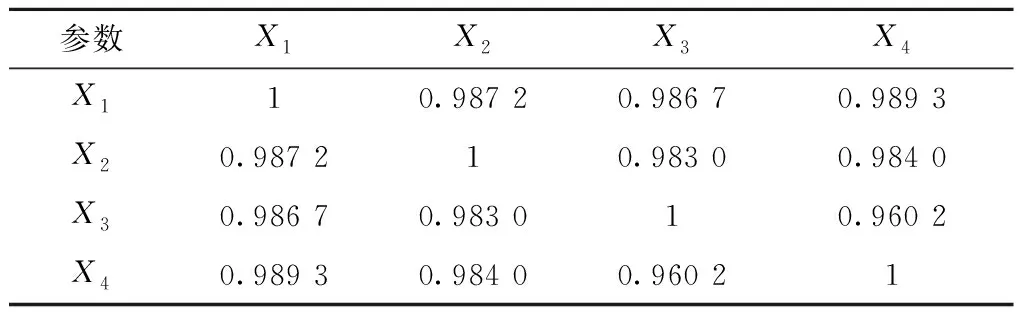
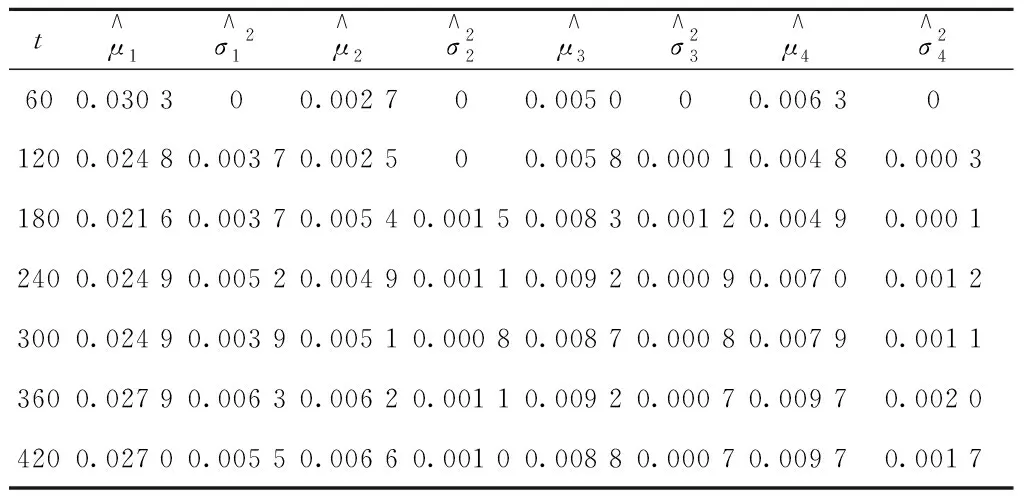
式中vab=Cov(ya(t),yb(t))是两个随机变量a与b之间的协方差Cov(ya(t),yb(t))=E[(ya(t)-μa(t))(yb(t)-μb(t))]。vab∈[0,1],当vab=1时,说明两个性能参数之间完全线性相关;当0 (4) Δxij~N(μΔtij,ΔtijΣ)。 式中:μ为各个性能参数μ组成的矩阵,Σ为多个性能参数的协方差矩阵。由于所有产品的所有性能参数都是在等距离时间下测量得到,则Δtij=Δt,令μΔ=μΔt,ΣΔ=ΔtΣ;则Δxij~N(μΔ,ΣΔ)。可以运用多元正态分布的性质来估计μΔ和ΣΔ,即: (5) 则可以得到: (6) 不同级别的健康状态可以认为是对应于不相同的健康模式,所以装备的健康状态评估相当于模式识别问题。采用基于距离的度量标准来解决该模式识别问题,不仅可以有效的将装备健康状态进行分类评级,而且可以将装备趋近完全故障(或偏离绝对健康)的程度定量描述,具有较好的实践意义。因此,运用距离进行健康状态空间划分,待测样本与健康样本之间距离值越小,说明其对应的装备状态越健康;反之距离值越大,表明对应的装备健康状态越差,也就愈接近于失效或故障。常用的距离测度有绝对值距离、欧氏距离、切比雪夫距离、兰氏距离和马氏距离等。本文利用马氏距离来划分健康状态空间。 设正常状态下的特征数据表达为Xi=(Xi1,Xi2,…,Xim),其中Xij表示第i次监测的第j个特征。建立一个标准的样本矩阵: 首先将每个特征数据标准化,一般标准化的方法主要有min-max标准化,z-score标准化和Decimal scaling小数定标标准化。本文选用z-score标准化,即 最后得出标准化后观测数据的马氏距离: 一般情况下,如果所观测性能合适,且马氏距离适用,不正常性能值的MD值会比正常性能值的MD值高。MD值越高则表示装备性能退化越厉害。将装备的健康状态划分为5个区间,即健康、亚健康、正常、劣化、故障。 (1)健康 装备所有性能参数均在正常范围内,系统能够完全正常运行,与出厂时的状态相差微小,离故障还有较远时间。 (2)亚健康 装备出现少量质量缺陷,但性能参数值远未达到性能阈值,有性能退化的迹象。 (3)正常 可以看出有性能退化的趋势,在接近规定性能阈值,此时可以提出检修计划。 (4)劣化 十分靠近或已经达到性能阈值,明显可以看出性能退化趋势,质量缺陷的情况可能已出现过多次,发生故障概率已大大增加,如果在实际工作中应该停止使用,并进行维修。 (5)故障 部分或者所有检测的性能参数已超过性能阈值,装备已完全不能实现其原有的功能,此时已无维修的必要。 将测量到的性能数据和基于维纳过程预测出的性能数据进行标准化: 进而计算MD值: 通过经验假设不同状态空间之间的界限所对应MD值,经过反复实验验证来最终确认分界的MD值,则可以达到定量评判每个性能值所对应的装备健康状态空间的位置。 TOPSIS是由Hwang和Yoon在1981年首次提出,是一种根据评价对象与理想目标的接近程度进行排序的方法。逼近理想解法主要通过构建理想解,计算各对象与正、负理想解距离,进而排序对比得出对象优劣性。本文将马氏距离与逼近理想解法相结合既可以有效地反映出各性能指标之间的关系,又能用一种直观科学定量的方法来评估装备健康状况。基于TOPSIS的健康状态评估流程如图1所示。 具体评估步骤如下: 步骤1构建样本数据的评价矩阵。 其中m指研究对象的个数,n指属性指标的个数。xij指的是第i个评价对象的第j个属性指标所对应的值(i=1,2,…,m;j=1,2,…,n。) 步骤2对矩阵A规范化处理。排除不相同的属性指标之间数量级与量纲影响,以此解决属性指标不可统一度量的问题。 式中rij指第i个评价对象的第j个指标下经过规范化处理后的值。 步骤3计算价值矩阵。 步骤4确定正理想解S+和负理想解S-。 其中,对于效益型指标Cj(指标值越大最后所得绩效越高的指标): 丨1≤i≤m}, 对于成本型指标Cj(指标值越小最后所得绩效越高的指标): 丨1≤i≤m}, 步骤5计算各对象与正理想解、负理想解的马式距离。计算第i天性能值Ai到S+和S-的马氏距离。 (7) d(Ai,s+)= d(Ai,s-)= 步骤6计算各评价对象的相对贴近度。 夏热冬暖地区装配式民用建筑混凝土预制外墙板热工性能分析 赵立华 段骁健 郑林涛 等 2018/02 46 (8) 数控机床进给系统试验平台(如图2)具有X、Y两个方向的运动,X、Y方向的行程为300 mm×500 mm,500 mm行程以内的重复定位精度为5 um。采用半闭环伺服运动控制,通过光栅尺测试工作台实际位置,能动态实时获取各轴运动到设定位置时旋转编码器和光栅尺位置差值,每隔一段时间(0.5 ms~100 ms可调)获取一组测量数据。每隔2个月(60天)进行一次检测,选取Y轴位移为检测对象。性能退化数据如表1所示,其中Y1为双向定位精度,Y2为双向重复定位精度,Y3为反向间隙误差,Y4为直线度。 表1 精度和误差测量值μm 性能060120180240300360420480阈值Y114.2016.0217.1718.0820.1821.6724.2325.5626.8928.40Y24.154.314.455.125.335.686.376.947.348.30Y33.804.104.505.306.006.407.107.508.207.60Y43.924.304.504.805.606.307.408.008.907.84 Xi(i=1,2,3,4)为性能退化量,即某时刻性能测量值与初始值的差值:Δxi=X(tj)-X(t(j-1)),Δxi为设备在时刻t(j-1)和tj之间的性能退化量。Δt=tj-t(j-1)为测量时间间隔。根据式(2),得到单性能维纳过程(如表2)。 表3 单性能维纳过程的退化量预测结果 μm 首先判断4个性能参数的相关性,如表4可见性能参数之间线性相关。所以按照性能参数线性相关的计算方法来计算。 表4 性能参数之间的相关系数表 Δxijk为第i个产品在ti(j-1)k时刻和tijk时刻之间第k(k=1,2,3)个性能参数的退化量: Δxij1=Xij1-Xi(j-1)1= [1.82 1.15 0.91 2.10 1.49 2.56 1.33], Δxij2=Xij2-Xi(j-1)2= [0.16 0.14 0.67 0.21 0.35 0.69 0.57], Δxij3=Xij3-Xi(j-1)3= [0.30 0.40 0.80 0.70 0.40 0.70 0.40], Δxij4=Xij4-Xi(j-1)4= [0.38 0.20 0.30 0.80 0.70 1.10 0.6]。 则Δxij表示为Δxij=(Δxij1Δxij2Δxij3Δxij4)′。 根据多元维纳过程的性质能推出Δxij服从多维正态分布,即: Δxij~N(μΔtij,ΔtijΣ)。 Δtijk=tijk-ti(j-1)k=Δt=60,从而可以得出: 进而可以推出: 表5 多性能维纳过程的退化量预测结果 μm 表6 多性能融合维纳过程预测结果 μm 根据表1所示性能参数测量数据进行健康状态计算。具体步骤如下: 步骤1构建样本数据的评价矩阵: 步骤2规范化处理和构建价值矩阵。4个性能退化数据是X和Y轴方向的运动数据,都是位移(或偏差),因此量纲相同。对于数控机床来言,X、Y方向的运动同样重要,都直接影响机床的加工特性,所以认为权重相同。由于量纲相同,权重赋值也相同,价值矩阵即为评价矩阵。 步骤3确定正理想解与负理想解。性能数值越小表示退化得越小,以性能状态最优为正理想解,退化程度越严重为负理想解,可见,这4个性能项均为成本型指标。以t=0时的性能参数值为正理想解,根据4.2节预测4个性能项性能参数值,当t=480时有性能参数达到性能阈值,此时可设定为失效状态,以t=480时的性能参数值为负理想解,则 S+={14.2,4.15,3.8,3.92}, S-={26.89,7.34,8.2,8.9}。 计算多个性能参数之间协方差矩阵Σ: 求协方差矩阵∑的逆Σ-1: Σ-1= 步骤4求解各性能数据的马氏距离和贴近度: 其中Ai为第2i(i=1,2,…,7)个月4个性能项的测量数据。 A1=[16.02 4.31 4.1 4.3], S+={14.2,4.15,3.8,3.92}, S-={26.89,7.34,8.2,8.9}, 同样地,计算得出其他时间马氏距离与贴近度,结果如表7所示。 表7 试验平台不同时间贴近度 续表7 步骤6对贴近度进行排序。贴近度越大反映综合性能越优,越小则反映综合性能越差。 从图3可以看出,第2个月试验平台为轻微退化,第4到10个月处于中度退化,退化程度随时间递增,到第12个月平台已严重退化,第14个月平台失效。同时,本文利用隐Markov模型对以上试验平台进行健康状态评估,图4为基于隐Markov模型的健康状态评估结果,可见第12个月劣化状态概率已达50%,故障的发生率增加,很快出现失效。可见,基于隐Markov模型的健康状态评估结果与本文的基于马氏距离的空间划分健康状态评估结果一致,但基于隐Markov模型的健康状态评估反映某时刻各种健康状态的概率,不能明确装备在某时间段的健康状态,本文的评估方法则可以确定装备在某时间段的健康状态。 本文针对机电装备的健康状态评估方法进行了研究,提出多性能融合维纳过程的性能退化建模方法,实现多性能退化量的预测。利用马氏距离划分健康状态空间,并提出基于TOPSIS的健康状态评估方法,判断机电装备在某时间段的健康状态。最后,通过实验,对数控机床进给系统试验平台健康状态进行评估,通过一系列计算分析证明了本文方法的准确性与有效性。未来将研究优化多性能参数相关性的方法,解决多性能融合维纳过程中计算量较大的问题,并继续研究健康状态空间划分策略,提高客观性评判标准的精准化。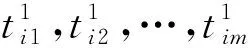
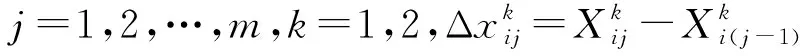
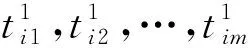
2 基于马氏距离的健康状态空间划分
2.1 状态特征矩阵构建
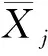

2.2 空间划分
3 基于逼近理想解法的健康状态评估
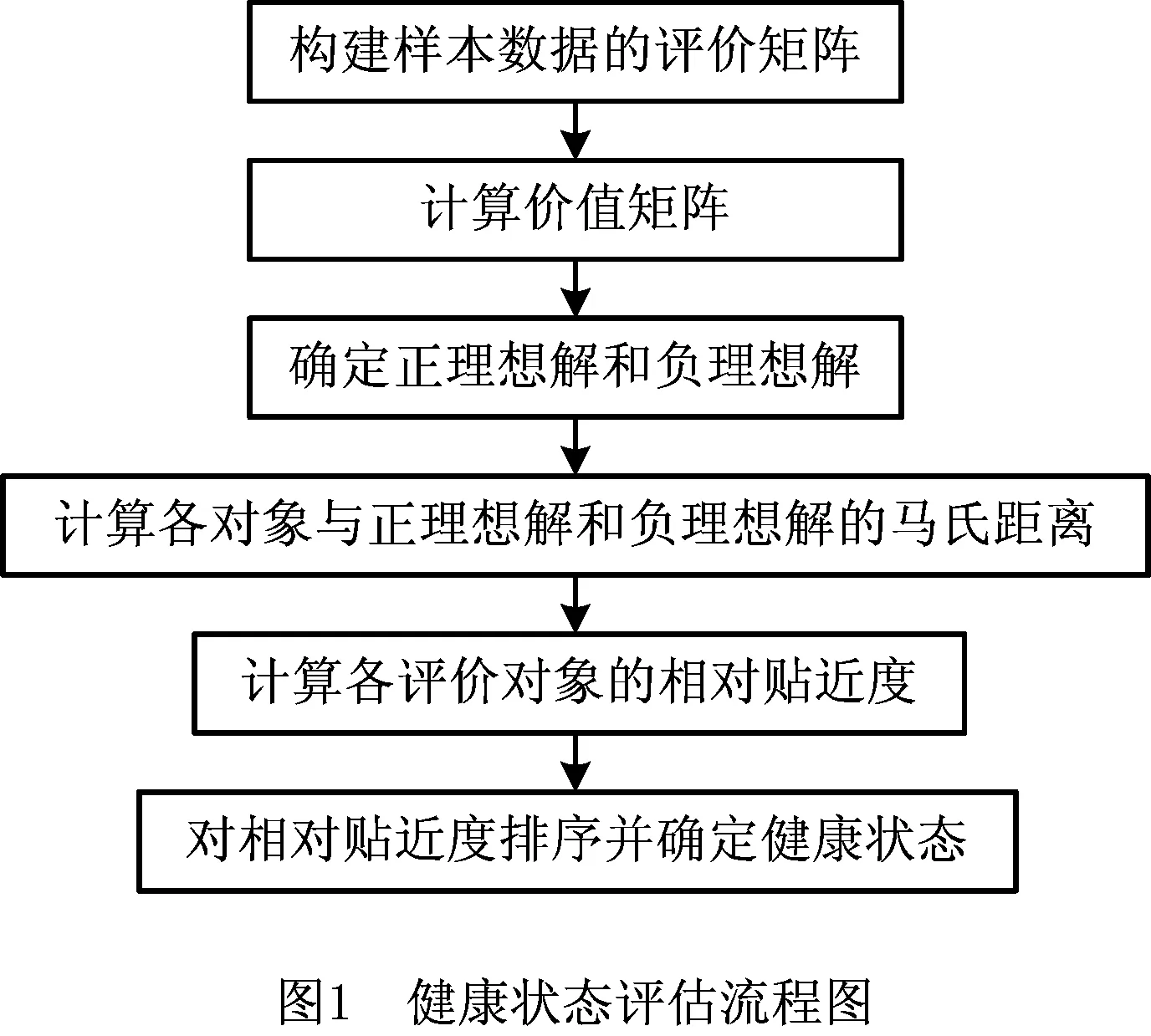






4 实验验证

4.1 单性能维纳过程
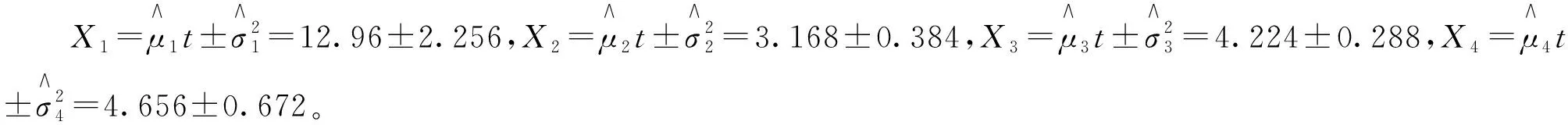

4.2 多性能融合维纳过程



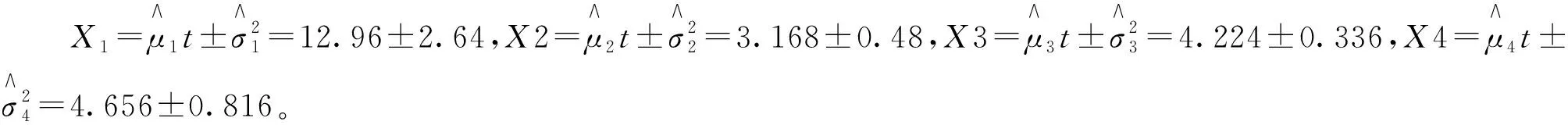

4.3 健康状态评估实验分析







5 结束语
