基于时间序列的装备制造企业采购策略优化
2018-10-18陈志鹏郭顺生
陈志鹏,彭 兆+,郭顺生,王 磊
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.武汉理工大学 湖北省数字制造重点实验室,湖北 武汉 430070)
1 问题的提出
装备制造业是一种先进制造业,主要为国民经济和国家建设提供各种类型的生产技术装备,如矿产资源的井采及露天开采设备,大型火电、水电、核电成套设备等,这些装备都具有大型且结构复杂的特点。而在目前的市场环境下,为了满足客户定制需求,企业又需要按订单对产品进行个性化设计,从而造成了同类型产品的差异化。在对这些定制产品进行生产时,产品生产工艺和资源需求量各不相同,对生产资源进行采购时,传统的采购策略难以适应这种复杂的情况。因此,根据产品的生产计划来优化生产资源的采购策略、降低生产成本,是本文要研究的问题。
在制造业的生产成本构成中,生产资源的库存成本作为主要控制对象,近年来引起了国内外研究学者的广泛关注。GREEN[1]和LABY[2]在JIT(just in time)模式下对影响企业采购效率的主要因素进行了分析,前者分析了企业在运用传统采购模型时遇到的问题,并针对这些问题提出了新的解决方案来提升企业的采购效率;后者分析了企业决策过程对采购效率和库存的影响,并在已有研究的基础上提出了基于多仓库协同采购的混合模型。MOROZOV[3]等基于项目导向型组织进行考虑,对项目实施过程中的生产资源供应问题进行研究,提出了同时优化项目管理与企业流程的概念模型。采购策略会影响企业的库存成本和生产成本,为准确计算库存成本,纪鹏程[4-5]研究了在复杂环境下对库存成本精确建模的方法,并结合钢铁企业原材料占用大量企业资金的情况,研究了在随机提前期和多品种多供应商供货的环境下,对企业库存成本进行精确建模的问题。陈铓[6]在连续时变需求下对可维修备件的库存进行了优化,降低了其总库存成本。周凌[7]在单周期按订单组装(Assemble-to-Order, ATO)的生产模式下,利用BASS扩散模型对客户订单进行预测,建立了组装厂商的利润时间连续模型来优化生产库存。以上研究初步讨论了生产与库存间的优化关系,RUAN[8]则进一步提出要考虑库存状态来制定批量采购策略。刘春玲[9]也建立了采购决策模型来优化不同部件的采购批量和采购周期。这些研究对库存成本进行精确分析,逐步将库存控制与采购策略优化相结合,通过建立模型来求解较优的采购策略,以降低库存成本,取得了一定的效果。但这类研究在考虑库存成本时不是从单个订单或项目出发,而是假设企业对资源的需求符合一定的分布规律,并建模优化订货批量和订货点,因此对于订单生产型制造企业的适用性较差。
国内外学者在近期的研究中将采购与生产相结合来进行考虑。夏海洋等[10-11]在研究供应商与采购商之间的采购关系时,考虑两方的共同利益,建立了生产-库存联合优化模型,运用该模型来求解单供应商和单采购商的生产-库存联合优化问题,并给出了求解最优生产批量、最优再订货点和订货量的优化算法。付开放[11]在OEM(original equipment manufacturer)供应商的产出率具有学习效应与遗忘效应的情形下,建立了采购商与供应商的集成决策成本模型。郉香园等[12]提出将物料采购和生产过程协同管理,以过程协同控制为核心,建立了采购物料协同控制模型。ALFIERI等[13]利用生产计划来提取资源需求信息,制定资源采购计划。DIXIT等[14]对复杂产品的生产工序进行分析,研究了生产时间不确定时库存成本的优化问题。TABRIZI等[15]和FU[16]研究了同时规划项目生产和资源采购的问题,为了降低生产成本,TABRIZI将生产时间和生产费用的不确定性作为影响因素进行考虑,建立了混合整数模型,并将这两个因素的不确定性作为模型求解的限制条件;FU全面考虑了生产过程中的资源价格、订货费用和库存费用,建立了成本模型,并求得最优的采购策略,为项目经理提供运营建议。在对模型进行求解时,以上两者均在约束条件下,利用基于遗传算法的混合启发式算法来求解。DAI等[17- 18]以项目为对象,从原材料价格波动方面来考虑库存成本问题,并将项目的整个周期分成几个阶段,分别优化每个阶段内的资源采购策略。DAI在对原材料价格进行预测的基础上,对各采购时间点的资源采购量进行优化;SHU针对不同的价格区间和资源需求量分别优化采购策略。综合考虑生产过程和采购策略来降低生产资源的库存成本,已逐渐成为降低生产成本的主要途径,引起了各方学者的关注。
综上所述,目前的研究主要考虑资源价格的波动和需求分布规律两个因素,来建立成本控制模型,并求解最优采购批量和订货点。部分研究考虑了生产排产和采购流程等因素进行优化,但没有针对装备制造行业的特性进行研究,这类以订单生产为主要生产方式的企业,更加注重生产成本的控制。本文对这类企业进行了研究,发现在生产资源的采购和管理方面存在以下问题:①企业经常超前采购一些价格高、精密度高且较难保管的资源,增加了资金占用成本和库存管理成本;②对部分资源的采购不及时,造成了生产延误损失。为了解决这些问题,本文首先分析了产品生产计划和资源需求信息,然后考虑采购资金占用成本、库存管理成本和缺货成本,建立了库存成本优化模型;并利用启发式算法求解最优采购策略,整个流程如图1所示。
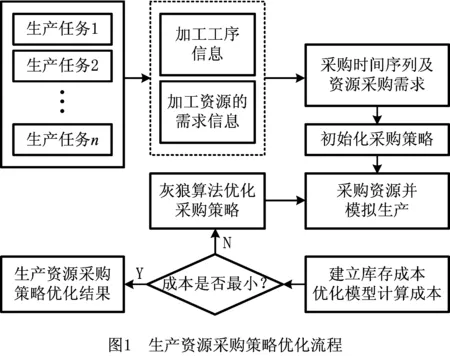
2 生产资源采购策略优化
2.1 问题描述及变量定义
装备制造企业的产品是客户定制化的大型复杂设备,具有生产周期长、资源消耗量大的特点。在多产品并行生产过程中,各产品的加工工艺不同,对各种资源的需求量也不相同,制定合适的采购策略来配合生产,并尽量降低成本,是一个十分复杂的问题。在不能确定采购时间节点的情况下,本文参考之前的相关研究[19-20],提出基于时间序列的生产资源采购策略优化方法。首先通过生产计划来获取采购时间序列,然后建立库存成本优化模型,优化基于时间序列的生产资源采购策略。
假设有产品a和b需要生产,根据生产计划获取生产工序的相关信息;则通过生产计划来获取采购时间序列可分为4步:
(1) 提取各道工序的开始日期和结束日期,形成工序时间点集合。
(2) 以天为单位建立时间坐标轴,将工序时间点集合中最早的工序开始日期所在月份的第一天设为坐标原点,最晚的工序结束日期所在月份的最后一天作为终点。两者间的时间跨度即为工序集合的时间跨度,记为k。
(3) 将各道工序的开始日期映射到坐标轴上,获取对应的坐标,作为采购时间点集合,如{3,27,56,…}。
(4) 选取坐标集合中互不相同的时间点并排序,作为采购时间点集合,称该集合为采购时间序列。
本文考虑生产资源的采购资金占用成本、库存管理成本和生产延误成本来进行建模,结合企业实际作如下假设:
(1) 企业生产产品时按工序段进行,各工序段的加工顺序有先后约束。
(2) 企业的库存空间、采购资金等库存资源不作为采购策略的限制条件。
(3) 在生产进行过程中,只考虑生产资源供应情况的限制。
(4) 在不考虑采购提前期的情况下,本文优化的采购策略中使用的采购时间点为到货日期。
在满足以上假设的情况下,基于时间序列的生产资源采购策略优化问题可以描述为:设在某段时间内,产品生产任务集合为T= {t1,t2,…,tn},生产资源种类集合定义为R={r1,r2,…,rm},工序集合定义为P={p1,p2,…,pg}。通过某几道加工工序pi的组合,可以完成生产任务ti,而完成每道工序pi需要一定种类和数量的生产资源ri。下面建立基于时间序列的库存成本优化模型,来优化生产资源的采购策略,为了方便模型的建立,设定如下变量:
I为企业资金投资日均回报率;
N为灰狼种群的灰狼个体数量;
u为库存成本优化模型中成本项目的个数;
Ei为库存成本优化模型的第i个成本项目;
f为企业单次采购的固定成本;
rpi为生产资源i的单价;
ici为单位时间内单位数量的生产资源i的库存管理费用;
dpi为任务i的单位时间延期损失;
psij为任务i的第j道工序开始时间;
peij为任务i的第j道工序结束时间;
rbij为企业在时间点i对生产资源j的采购量;
ipi表示在时间点i是否进行采购;
teij表示生产任务i在第j天的工作量是否完成;
rqij为生产资源j在时间点i的库存量;
dti为任务i的生产延期时间;
Oc为资金占用成本;
Mc为生产资源库存管理成本;
Dc为生产延误成本;
F为生产资源的总库存成本。
2.2 库存成本模型建立
建立库存成本优化模型,并构建如下评价函数:
(1)
式中:u=3,E1=Oc,E2=Mc,E3=Dc。
(1) 资金占用成本(Oc)是指采购占用企业资金时产生的机会成本。采购占用的资金即采购成本,包括固定采购成本和可变采购成本。固定采购成本即每次采购都需要支出的固定费用,记为f;可变采购成本与采购资源的数量相关,即所采购的生产资源总价。
(2)
(3)
式中:h为采购时间序列中采购时间点的个数,tsi为第i个采购时间点与最晚采购时间点的时间间隔。
(2) 库存管理成本(Mc)由生产资源的在库量决定,是指企业库存资源的管理费用,
(4)
(3) 生产延误成本(Dc)是指由于生产资源采购不及时,而造成的生产延误损失,
(5)
(6)

结合企业实际,要求采购的生产资源数量必须满足生产任务对资源的需求总量。为此,采用罚函数法结合上述评价函数,构建无约束的广义目标函数:
北京市160人次;江苏省98人次;广东省49人次;上海市47人次;浙江省45人次;湖南省37人次;山东、河南两省各31人次;湖北省29人次;四川省23人次;辽宁省15人次;福建、吉林两省各14人次;陕西、贵州两省各13人次;安徽、甘肃两省各12人次;云南、河北及天津市各10人次(10人次以下省市从略)。在本次统计范围内,我国大陆的省级行政区,除了青海省和西藏自治区外,各省市都有供职于不同机构的研究者参与社会治理研究,并有数量不等的论文得以在国内发表。共有721篇有关文献标注了作者供职机构,占本次统计范围内有关文献总量的81.652%。
F(x)=F+δ(gen)H(x)。
(7)
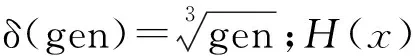
本文根据解违反约束条件的程度,来确定惩罚力度;采用PARSONPOULO[21]提出的一种非固定多段映射罚函数法来动态确定惩罚因子,并结合本问题调整了相应的参数,具体调整如下:
(8)
qj(x)=max{0,pj(x)},
(9)
pj(x)=hj(x),
(10)
hj(x)=|npj-rpj(x)|,
(11)
(12)
(13)
staj=0.05npj。
(14)
式中:rpj(x)是采购策略对第j类资源的采购总量,npj是生产任务对该类资源的需求总量。考虑到资源运输损耗及质量波动,企业在采购资源的时候允许超量采购,超量标准一般为需求总量的5%~10%。本文将分段映射函数的分段间隔设为资源需求总量的5%,如式(14)所示。
3 基于IGWO算法的优化求解方法
灰狼优化(Gray Wolf Optimization, GWO)算法是MIRJALILI等[22]于2014年提出来的,该算法模仿灰狼种群的领导层级和捕食机制,将狼群个体分为α、β、δ、ω四种类型;并将狼群的捕食活动分为寻找猎物、包围猎物和袭击猎物3个步骤。
3.1 参数定义
GWO具有较好的计算鲁棒性和全局搜索能力,在函数优化方面,已被证明在求解精度和收敛速度上均优于粒子群优化算法和遗传算法[23-24]。本文所要求解的采购策略矩阵是一个二维矩阵,可将其作为灰狼个体的位置坐标进行优化,故本文选用GWO作为求解算法,并对主要的矩阵变量定义如下。
定义1工序时间矩阵PT。PT矩阵描述了各道工序的开始和结束日期。定义PT=[PS,PE],其中:PS为工序的开始日期矩阵,PS=(psij)n×g;PE为工序的结束日期矩阵,PE=(peij)n×g。元素psij和peij分别表示第i个生产任务的第j道工序的开始日期和结束日期,如果生产任务i不存在工序段j,则对应位置的矩阵元素为0。
定义2资源采购策略矩阵RB。RB矩阵描述生产资源采购策略,表示在采购时间序列中的各个采购时间点对各类资源的采购量,
RB=(rbij)h×m。
(15)
式中:h为依据采购时间序列获得的采购时间点的数量,m为生产资源种类数量。
资源采购策略矩阵是本文的优化对象,为减少变量个数,需要对该矩阵做扁平化处理。由上文可知,RB的每一行代表在相应的采购时间点对各类资源的采购量。从上至下对每一行所对应的采购时间点按月进行分组,统计在小组内的各个采购时间点开始加工的工序,并汇总工序对各类资源的需求量。选择需求量最小的资源作为该组的优化对象,以确定在该小组内的每个采购时间点对该资源的采购量,之后按照工序对其他资源的需求量与对该类资源的需求量的比例关系,等比例地计算在每个采购时间点对其他资源的采购量。如此,一个RB矩阵可以被处理成为一个h×1维的矩阵,作为一个灰狼个体的坐标,故灰狼种群的位置坐标的形式为X=xij(i=1,2,3,…,h;j=1,2,3,…,N)。
定义3生产资源库存量矩阵RQ。RQ描述生产资源的库存量,RQ= (rqij)m×k,其元素rqij表示第i类资源在第j天的库存量。
3.2 算法求解
运用库存成本优化模型来优化求解生产资源采购策略,需要输入的参数包括各个生产任务的工序信息、每道工序对各类资源的需求量及资源单价等,输出结果为优化后的生产资源采购策略。具体算法流程如图2所示。
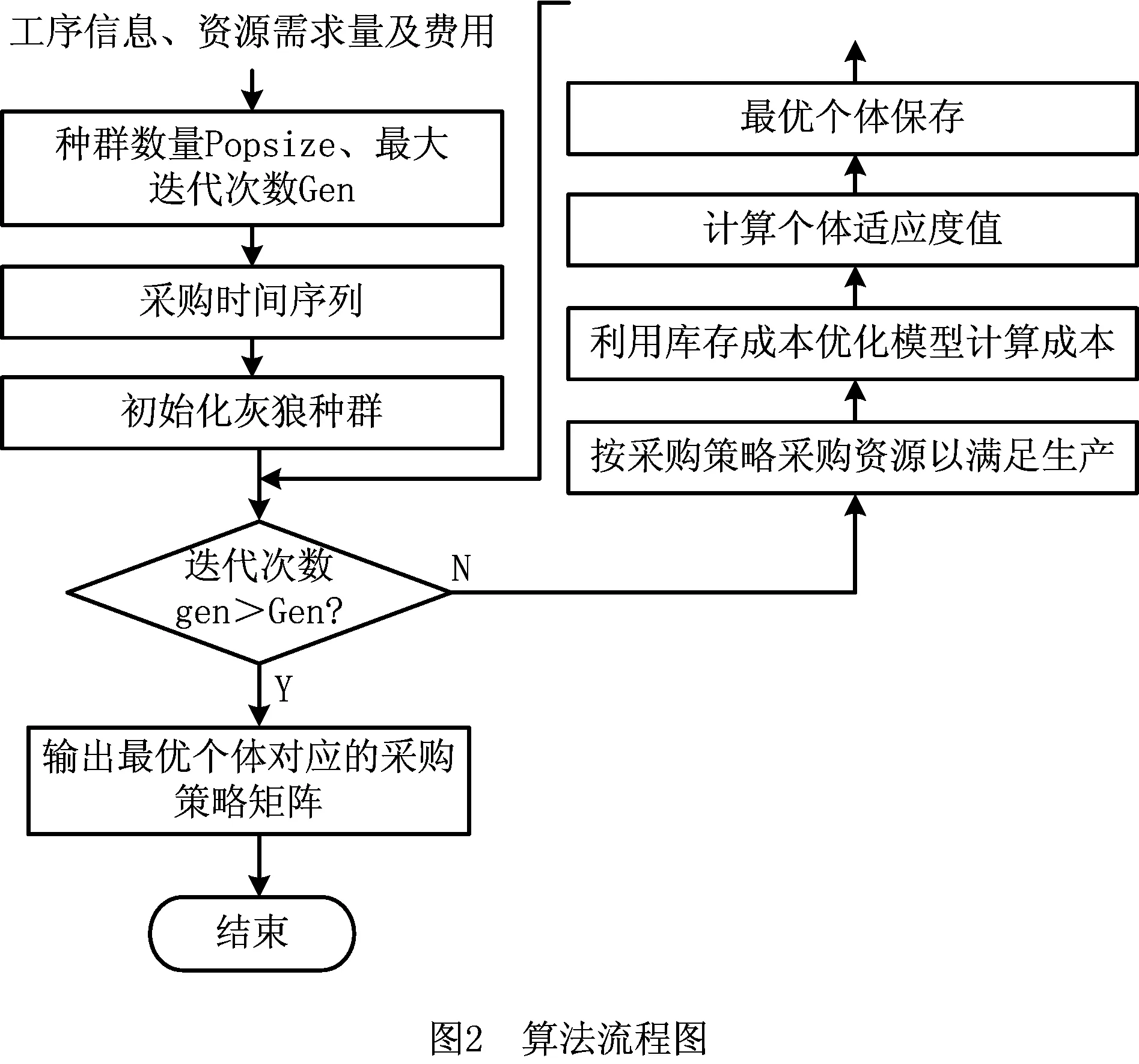
为提高算法效率,本文改进了原始GWO算法,提出改进灰狼优化(Improved GWO, IGWO) 算法,改进部分如下:
(1) 适应度评估 首先对灰狼个体坐标进行解码,得到采购策略,然后带入库存成本模型来计算库存成本,通过惩罚函数计算惩罚项,最后采用均一化方法将广义目标函数转化为如下适应度函数:
(16)
式中:X为灰狼种群的编码集合,x为灰狼个体的编码,Ocmin=minOC(X),Mcmin=minMc(X),Dcmin=minDc(X),Ocmax=maxOc(X),Mcmax=maxMc(X),Dcmax=maxDc(X)。在求解{Ocmin,Mcmin,Dcmin}和{Ocmax,Mcmax,Dcmax}时,利用初始种群对其初始化,在求解过程中与当前群体中的最小、最大值进行比较替换。
(2)位置更新 在GWO算法中,由α,β,δ执行追捕行为,ω跟随前三者对猎物跟踪围剿,最终完成捕食任务。在灰狼捕食过程中首先需要对猎物进行包围,计算每个灰狼个体与猎物之间的距离:
D=|C×Xp(t)-X(t)|。
(17)
式中:Xp(t)表示第t代时猎物位置;X(t)表示第t代时灰狼个体的位置;C为摆动因子,
C=2r1。
(18)
式中:r1为[0,1]上的随机数。
灰狼个体位置更新:
X(t+1)=Xp(t)-A×D。
(19)
式中:A为收敛因子,
A=2ar2-aD。
(20)
式中:r2为[0,1]上的随机数,a随迭代次数的增加从2线性递减到0。
在狼群接近目标的过程中,原始GWO算法的位置更新方程对α、β和δ表现出同等重要性,这种情形下α 狼的领导位置与最优解应占有的比例没有被体现出来。因此,本文使用新的位置更新方程,在创建一个与适应度值成比例的概率分布后,通过该分布来更新灰狼个体的位置:
(21)
(22)
式中:f(x)为灰狼个体的适应度值,X1,X2,X3分别是利用式(19)计算的个体以α、β和δ为目标移动后的坐标。
(3)灰狼变异 按照上述灰狼坐标形式进行优化,其结果可能会不符合要求,即在多个采购时间点对资源的采购总量都很小,这表明企业需要频繁地进行小批量采购,不符合实际需求。因此,在优化过程中要对最优灰狼个体进行变异处理,在上文所提到的采购时间点分组中,如果某个采购时间点的资源采购量小于特定值,要将该点的资源采购量加到同组内的其他采购时间点,此处的采购量设为0。依据灰狼坐标的初始化过程,可以计算出在平均分配方式下各个采购时间点需要采购的资源数量,即判断所需的特定值。这种变异操作不仅可以减少采购次数,还可以避免灰狼种群出现早熟和陷入局部最优解。
4 应用算例
唐山某建材装备制造企业是订单生产型企业,本文以其生产资源采购策略优化问题为例,对所提出的基于时间序列的生产资源采购策略优化方法进行验证。算法运行环境为IntelCore(TM) i3 CPU,主频3.6 GHz,内存4 GB,Windows7 64位操作系统,实验仿真软件采用MATLAB R2013a。
4.1 初始化参数及数据
假定在某一时刻,企业的生产任务集合为{t1,t2,t3,t4,t5},各生产任务的加工工序集合分别为{p1,p3,p4,p6,p7,p8,p9},{p4,p5,p6,p8,p9,p10,p11,p12},{p10,p11,p12,p13,p14,p15},{p3,p4,p5,p6,p13,p9},{p2,p5,p6,p4,p7,p3,p12},生产所需的资源种类有{r1,r2,r3,r4,r5,r6,r7,r8,r9,r10},甘特图如图3所示,图中矩形内的数字为工序编号,其他实例参数如表1~表3所示。

表1 生产任务数据

任务编号工序编号资源编号所需资源数量/kg日延期成本/元11,3,4,6,7,8,9,1;2,5;7;4,5,8;4;4;310;5,11;6;4,8,8;4;10;5100024,5,6,8,9,10,11,122,3;5,6;2,4,5;4;8;6;9;1,1010,20;4,8;4,16,15;2;8;45;12;10,81200310,11,12,13,14,151;3,5;1;7,9;5;1020;1,5;4;2,10;5;20100043,4,5,6,13,93,5;2;1;5,9;10;8,912,15;5;4;8,5;10;4,8150052,5,6,4,7,3,121;2;4,5;3;8;6;7,919;23;4,5;11;10;8;6,51300

表2 工序相关数据
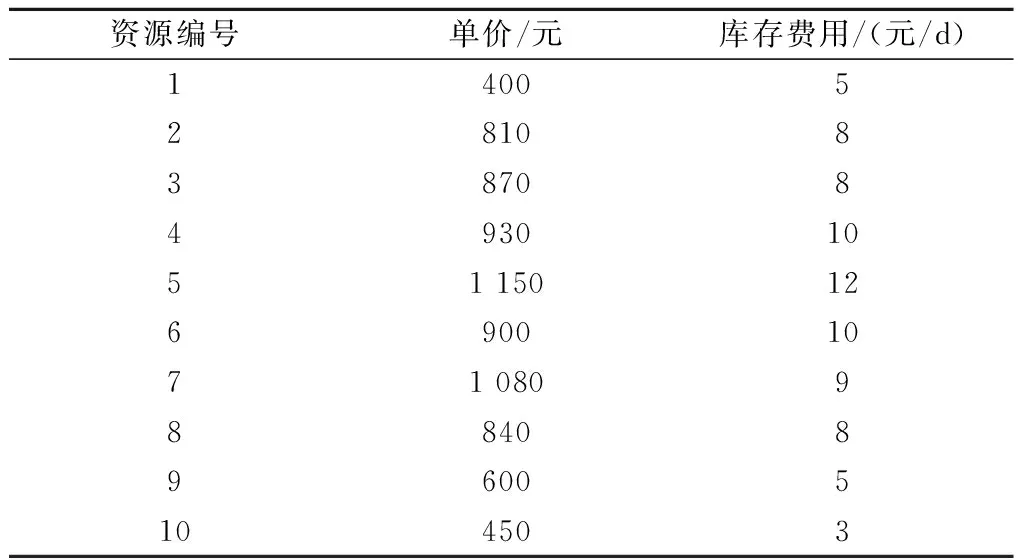
表3 生产资源相关数据
在上述实例参数的基础上,本文确定GWO算法的相关参数为:算法最大迭代次数Gen=300,群体规模PopSize=30,单次采购固定成本f=5000元。
4.2 算法运行结果及对比
经过10次算法计算,得到最低的总成本为170 620元,对应的(Oc,Mc,Dc)为(65 070,105 550,0),单位为元。将该算法同GWO、遗传算法(Genetic Algorithm, GA)和粒子群优化(Particle Swarm Optimization, PSO)算法进行对比,种群中最优个体的总成本进化曲线如图4所示。
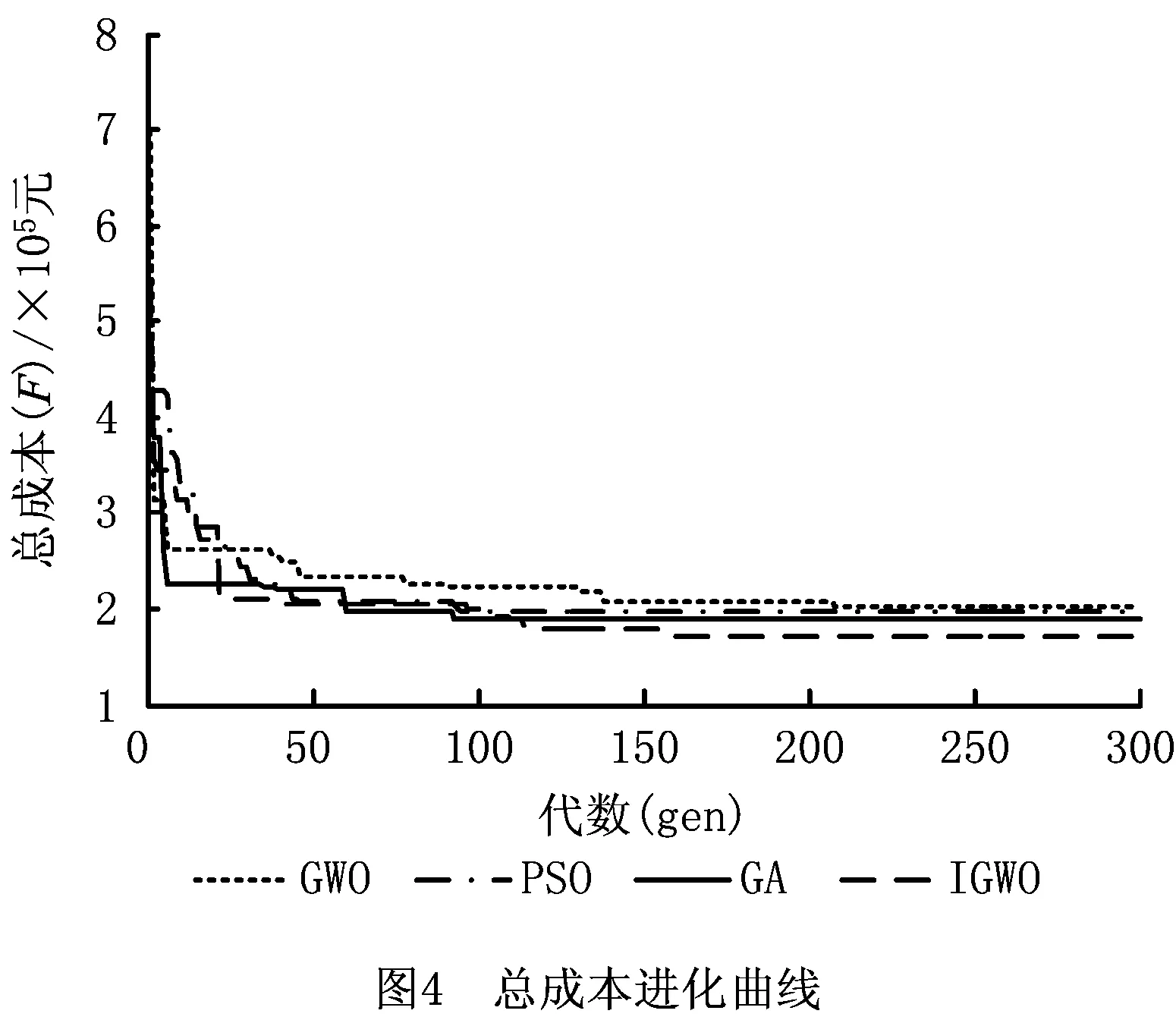
图4表示4种算法的成本曲线进化图。可以看出,4种算法都能快速收敛。与GWO算法相比,IGWO算法有更强的寻优能力,收敛速度也较快;并且在全局最优解的寻找能力上,IGWO强于PSO算法和GA。图5~图7分别表示利用IGWO算法进行优化时,资金占用成本、库存管理成本和生产延误成本的进化曲线;表4是优化之后的采购策略,结果表明需要在(8,10,50,80,115,145,160,207,242,277) 这几个采购时间点采购相应的资源。
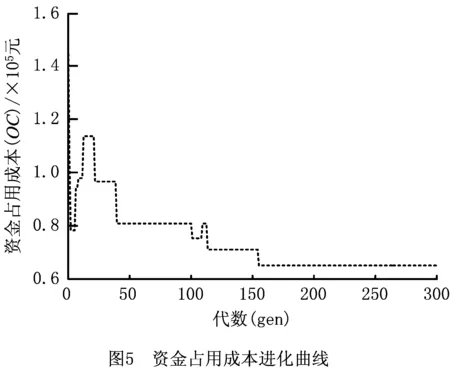
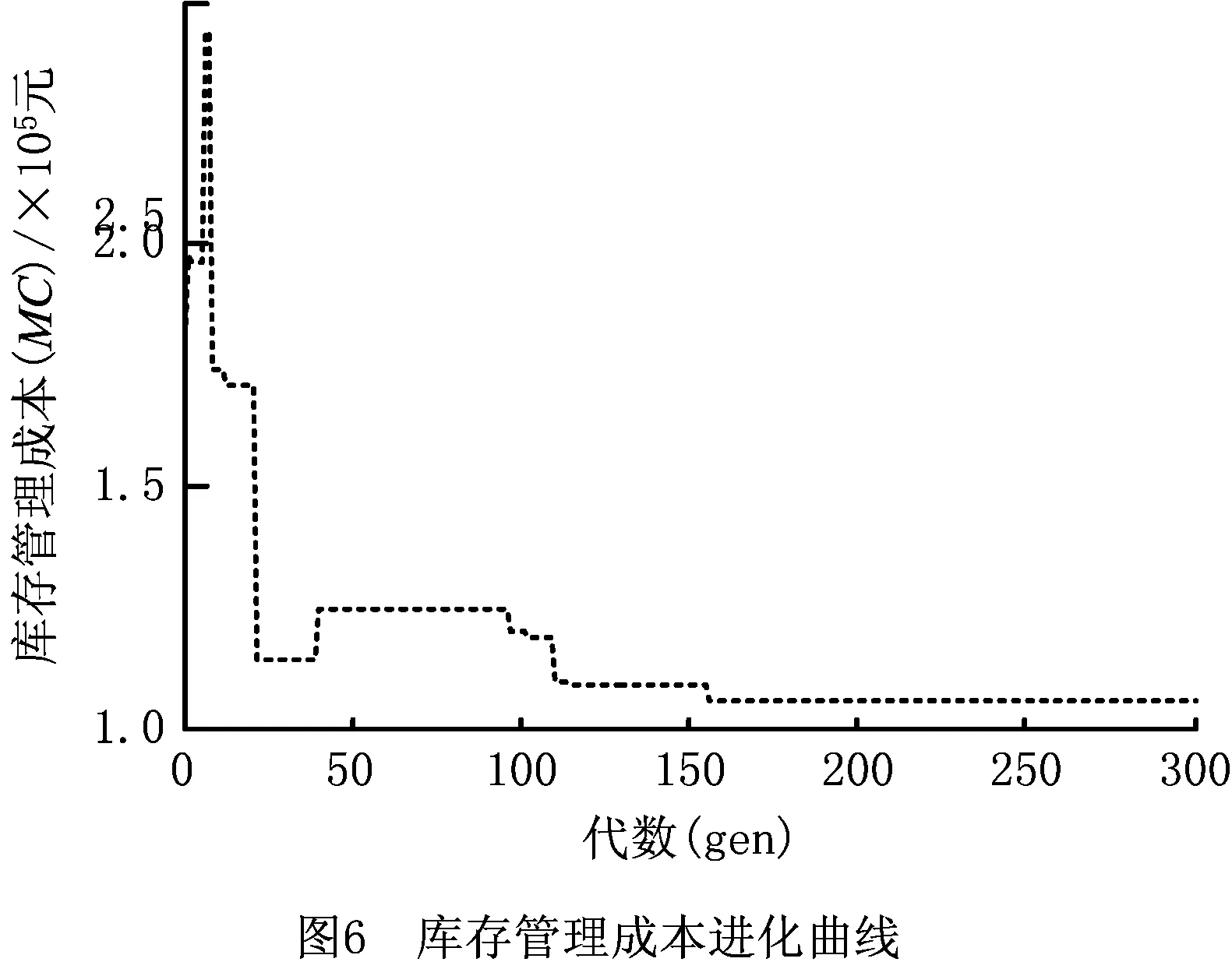
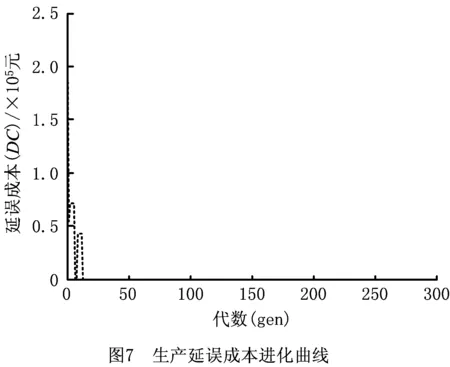
4.3 采购策略对比
从表5的库存成本对比可以看出,优化之后的采购策略能有效降低库存成本。因此,对于这种产品生产周期长、资源消耗量大的订单生产型装备制造企业而言,本文所提的采购策略优化方法比传统采购策略更有优势。
4.4 算法复杂度分析
本文针对装备制造企业采购策略进行研究,问题集中在如何从h个不同时间节点中选出最佳采购时间节点及对应的m种资源的采购数量组合,使得制造过程总库存成本最低。问题规模大小可视作h×m,且h≤k,在装备制造企业实际背景下h< 表4 采购策略优化结果 表5 采购策略成本对比 (1)初始化种群需要进行N×h次赋值运算。 (2)计算N个灰狼个体的适应度值。适应度值是Oc,Mc,Dc和惩罚项之和,计算Oc和惩罚项的复杂度是O(m×h);对Mc和Dc进行计算要先模拟生产过程,以得到相应的资源库存量信息和生产延误时间,故Mc的计算时间复杂度为O(k×m),Dc的计算复杂度为O(n×k),惩罚项的计算复杂度为O(h×m),则个体适应度计算复杂度为O(m×h+n×k+k×m+h×m),即O(m×k)。 (3)选择适应度最高的3项灰狼个体,计算复杂度为O(N×N)。 (4)位置更新及变异,计算复杂度为O(N×h×m)。 因此,在算法运行gen次时,最坏情况下算法的时间复杂度为O(gen×N×k×m+gen×N×N)。同理可求出算法的空间复杂度为O(k×m)。由此可见,算法求解时间将随工序集合时间跨度的增长而增加,随所需资源种类的增多而增加。当算法参数固定时,算法的求解时间与任一单独变量成线性关系,而非指数关系,因而适用于装备制造企业采购化。 为验证上述分析,本文固定算法参数,设计了对比实验。分别测量所需资源种类数为5、10、15,工序集合时间跨度为170、316、455时算法的运行时间,结果如表6所示。观察表中的数据发现,算法的运行时间与资源种类数线性相关,与工序集合时间跨度线性相关。 表6 算法时间复杂度分析 s 本文针对装备制造企业的生产资源采购策略进行优化,首先从生产计划中获取采购时间序列,之后考虑资金占用、库存管理和延误成本建立库存成本优化模型,并运用IGWO算法进行求解。该理论模型和求解方法具有以下特点和优势: (1) 结合装备制造企业订单生产模式的特点,以产品的生产任务为对象提出库存成本优化模型,能更加直观和有效地控制产品的生产成本。 (2) 采用时间序列的概念,以工序开始日期的集合作为生产资源采购策略的采购时间点集合,对采购策略初始化后,利用库存成本优化模型来优化采购策略。 (3) 鉴于GWO算法是一类基于无约束的优化技术,引入非固定多段映射罚函数法来构建广义目标函数,并改进了原始GWO算法。 本文针对企业某段时间范围内的资源采购策略进行优化,以满足该段时间内的产品生产对生产资源的需求,并降低成本,属于静态优化方法。但是在生产执行的过程中,任何生产异常或者资源价格波动都会对采购策略的实施产生影响,因此下一步的工作是将资源价格波动和生产异常等因素考虑进模型中。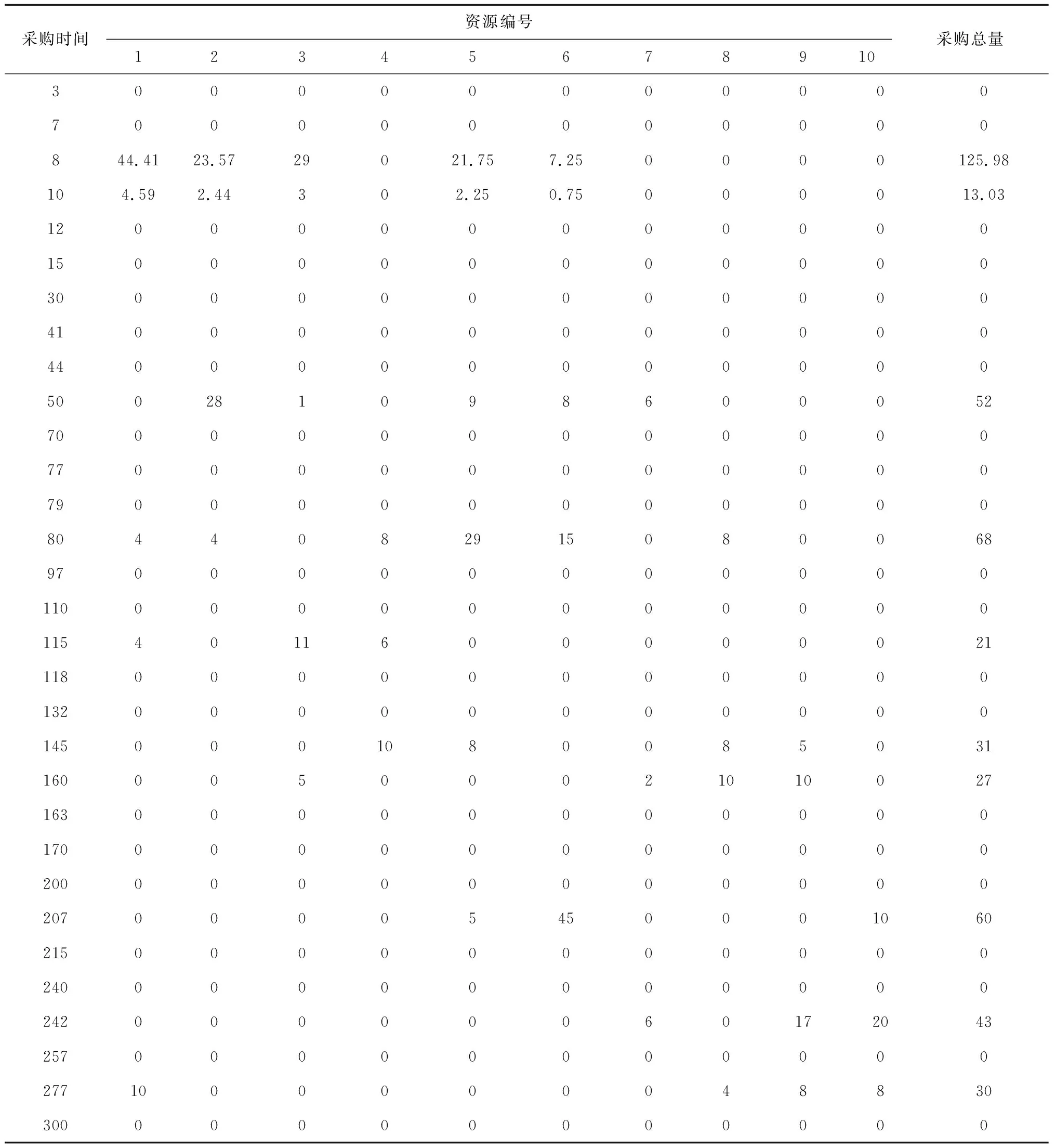


5 结束语
