Fe4N电子结构及其磁性

吴云沛，胡永金，周望怀

(湖北汽车工业学院 理学院，湖北 十堰 442002)

0 引 言

铁经过氮化处理后会形成各种各样的间隙性合金，可以大大改善材料的性能，一般具有饱和磁化强度、低的矫顽力、较高的磁导率等特点，是一种优良的自旋电子材料，因而对它的机理的研究越来越多。Kim等就用铁和氮化物反应生成了强磁性的Fe16N2，且有巨磁矩现象[1]。无论是在实验还是理论上，人们对铁的氮化物为什么有这么大的磁性有着各种各样的解释[2-4]。钙钛矿结构的Fe4N就是一种立方结构，可认为是N插入面心立方结构的γ-Fe中。不仅具有很强的磁性，而且很耐磨，还具有良好的热稳定性，可在磁记录、薄膜磁头和微波吸收等领域得到广泛应用，被认为是一种很有潜力的高密度记录材料，具有高矫顽力、高饱和磁化强度、高稳定性等优点。Mohn等用从头计算的方法研究了Fe4N的磁性随体积的变化，顶角Fe原子的磁矩随体积的增大而快速地增大，但面心Fe原子磁矩并不会连续的增加，而是存在着一个向高磁矩转变的过渡态[5]。早期，人们也用了一些实验方法如机械合金化、金属铁蒸发等制备出了Fe4N[6]，通过改变不同的制备条件来研究其磁性结果，以期望制备出具有良好磁性的电子材料[7-9]。王庆相等对纯铁粉进行气体渗氮，成功制备出了粉末状的Fe4N[10].Siberchicot等研究了氢的吸附对Fe4N物理性质的影响，当吸附一个H原子时，晶胞体积增大，磁性没有改变。但是，随着吸附H浓度的增加，顶角处和面心处Fe的磁矩都是迅速减小，晶体的总磁矩也随着减小[11]。Gil等研究了Fe4N的磁性和电子输运性质会随着应力的变化而变化[12]。Shi等研究表明，在Fe4N薄膜结构系统中，不同层面中的Fe和N原子间的杂化作用和键长大小都会对磁矩的大小产生较大的影响[13]。

前人的研究主要集中在体积变化、掺杂、应力应变对Fe4N的磁性性质的影响，但是缺乏对磁矩的微观来源、不同占位Fe原子的磁性强弱和N原子对整个体系的磁性贡献的研究。笔者采用基于密度泛函理论的第一性原理的平面波赝势方法，对Fe4N晶体结构进行了几何优化，还对每个原子的Mulliken电荷和磁矩进行了定量计算，并和前人的实验和理论结果进行了比较。最后，还从微观方面对它们的自旋劈裂态密度大小用Stoner模型进行了理论分析，对不同位置上的Fe和N产生不同的磁矩进行了很好的理论解释。

1 理论模型

在多原子体系中，Born-Oppenheimer近似能量的泛函形式为

(1)

对(1)式变分求极小值，可导出多原子体系的Kohn-Sham方程

(2)

式中μxc(ρ)为交换相关能Exc的微分。在(2)式中，μxc(ρ)可采用局域密度近似(LDA)或广义梯度近似(GGA)来自洽计算。具体来说，LDA[14]是利用均匀电子气的电荷密度函数ρ(r)来得到非均匀电子气的交换相关泛函

(3)

但是，GGA是在交换相关能中加入与电荷密度梯度或高阶梯度有关的项，它实际上是在完全局域的LDA交换相关能中引入电子交换与关联的非局域的贡献，其表达式用文献[15-16]中提出的广义梯度近似修正

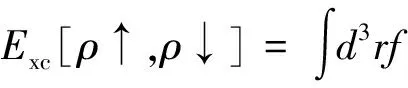
(4)

在晶体势场中，采用周期性边界条件后，电子轨道波函数满足Bloch定理，用平面波展开为

(5)

文中的计算是基于密度泛函理论下的平面波赝势方法(PWP)从头计算方法，对Fe4N晶体结构进行了几何优化得到其稳定的构型。这里采用的实验上测量出来的晶格常数[17]，立方体的边长为0.379 6 nm，其结构如图1所示，中心是N原子，面心和顶角是Fe原子的位置，相当于一个面心结构再在体心处加上一个N原子。为了更好地描述N和Fe之间的相互作用，把Fe原子分成2类：一种是位于顶角处个8个Fe原子，为Ⅰ类；另一种是面心上的6个Fe原子，为Ⅱ类。

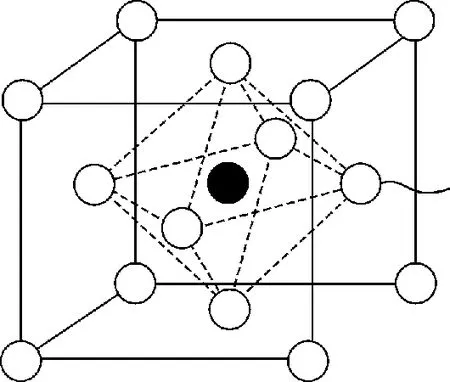
图1 Fe4N晶体结构Fig.1 Crystal structure of Fe4N

交换-关联能用广义梯度近似(GGA)来描述[18]，为了保证计算的速度但又要满足足够的精度，文中在计算时平面波截止能量(Cutoff energy)取400 eV，K网格(K-mesh)的大小取为4×4×4，原子间的相互作用力的收敛标准是0.005 eV/nm，能量的收敛标准是2.0×10-5eV/atom.文中的计算是用VASP程序完成[19-21]，参与计算的价电子：N为2s22p3，Fe为3d64s2，内层电子不参与计算。所有的计算结果都是在绝对零度下的理论值。

2 结果与讨论

表1给出了Fe4N的Mulliken电荷分布和自旋磁矩大小。计算结果表明，N作为一种电负性比较强的元素，它带0.75个单位的负电荷，自旋磁矩仅为0.06 μB，这个结果非常小，可以认为是几乎没有磁性。但是，在晶体结构中不同位置的Fe(Ⅰ)和Fe(Ⅱ)完全表现出不同的磁性，前者带0.07个单位的负电荷，自旋磁矩为2.94 μB；后者带0.27个单位的正电荷，自旋磁矩为2.32 μB.Frazer等用中子衍射的方法分别测量出顶角和面心处的Fe原子自旋磁矩为2.98和2.01 μB[22].在理论方面，Akimasa Sakuma等用LMTO方法计算出来的结果为3.07和2.03 μB[23]；Fernando等通过Hubbard-Stoner模型计算出来的结果为3.08μB和2.39 μB[24]；杨菁等用DV-XT的方法计算出Fe4N结构中Fe(Ⅰ)和Fe(Ⅱ)的原子磁矩分别为3.30和2.12 μB，且N的磁矩为-0.18 μB[25]。这里的计算值和前人的结果比较接近，所以文中的计算结果还是可信的。为了更好地探索不同位置的Fe原子产生完全不同的磁性的原因，表2还计算出了Fe4N晶体中沿着最近邻方向的2个原子的聚居数情况。对于N-Fe(Ⅰ)和Fe(Ⅰ)-Fe(Ⅰ)键，2个原子的距离较远，它们之间的相互作用力也较弱，所以聚居数几乎接近为0.N-Fe(Ⅱ)键的聚居数为0.63，是一种比较强的共价作用，而且Fe(Ⅰ)对Fe(Ⅱ)也有一定程度的共价作用，再加上Fe(Ⅱ)自身之间的离子作用，这样严重地影响了Fe(Ⅱ)磁矩的大小，所以它比Fe(Ⅰ)的磁矩小一些。

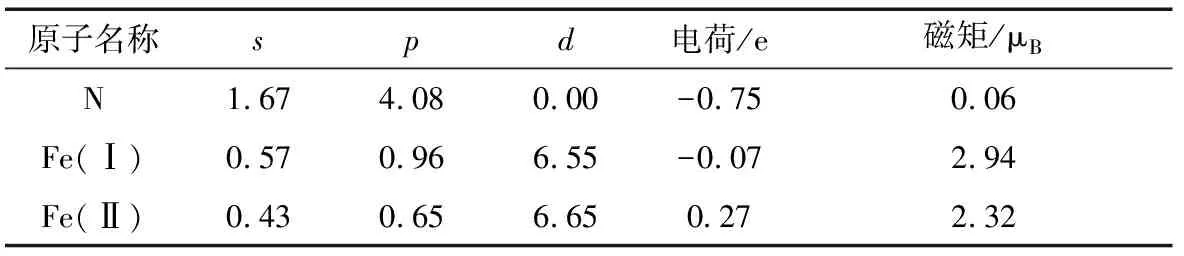
表1 Mulliken电荷分布和自旋磁矩

表2 聚居数分析

图2，3和4分别给出了Fe4N结构中N，顶角处Fe(Ⅰ)和面心处Fe(Ⅱ)的自旋劈裂态密度分布情况。在这里，只考虑N原子的s和p电子的情况。由于Fe是过渡金属元素，s和p电子的贡献较小，它的电子结构性质主要是d电子决定，所以主要关注d电子的态密度分布情况。为了方便观察和比较，把费米能级取作Ef=0 eV.根据过渡金属巡游电子铁磁性的Stoner模型，一个能带中的电子是否具有磁性，磁性强弱主要依赖于能带结构的态密度N(E)和磁相互作用能U大小。也就是如果电子间的磁相互作用越大，费米面处的电子态密度就越大，越容易产生磁性。通过比较N，Fe(Ⅰ)，F e(Ⅱ)态密度分布发现，在费米面附近，Fe(Ⅰ)和Fe(Ⅱ)的自旋态密度很大，而N的态密度要小很多，这就符合Stoner条件，就能够解释前文计算出来的Fe(Ⅰ)和Fe(Ⅱ)磁矩很大，而N的磁矩小的几乎可以认为是零。所以在Fe4N晶体中，整个体系的磁性贡献主要来源于铁原子。从图3和图4中可以看出，在费米能级附近，Fe(Ⅰ)的自旋劈裂程度要比Fe(Ⅱ)大一些，这也就是前者磁矩比后者的大一些的原因。

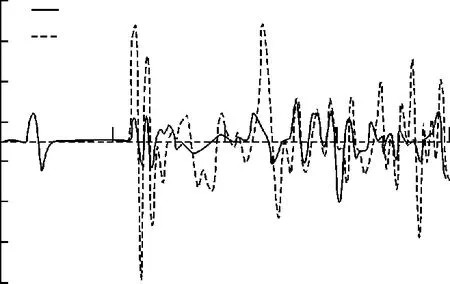
图2 N态密度Fig.2 Density of states of N

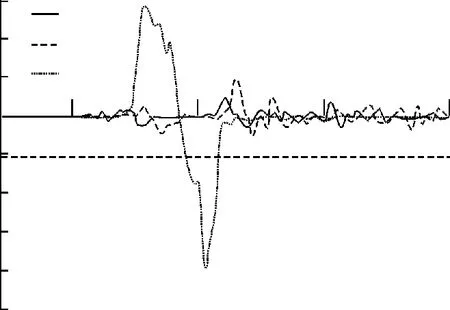
图3 Fe(Ⅰ)态密度Fig.3 Density of states of Fe(Ⅰ)

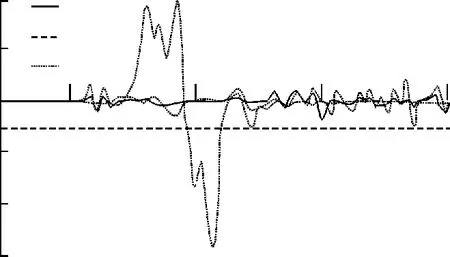
图4 Fe(Ⅱ)态密度Fig.4 Density of states of Fe(Ⅱ)

3 结 论

文中通过密度泛函理论下的平面波赝势方法，优化Fe4N晶体得到其稳定的结构，定量地计算出N，Fe(Ⅰ)和Fe(Ⅱ)的自旋磁矩的大小，数值与前人的实验和理论结果都符合得很好。这表明Fe4N晶体中的磁性主要来源于Fe原子，但是不同占位会影响其磁矩的大小。通过电荷聚居数分析，发现面心Fe(Ⅱ)和中心N原子存在着一种更强的共价相互作用，合理地解释了Fe(Ⅱ)的磁矩比Fe(Ⅰ)小的原因。另一方面，从它们的态密度图上，发现Fe(Ⅰ)劈裂程度比Fe(Ⅱ)要厉害一些，态密度值更大，运用理论上的Stoner模型也能够很好地解释Fe(Ⅰ)比Fe(Ⅱ)磁矩更大。所以，用这种平面波赝势方法来描述Fe4N的电子结构和磁性质还是非常成功的。文中的研究方法和结果为铁的氮化物的磁性来源和定量研究提供了很好的理论依据，下一步的研究对象在于类似的氮化物的磁性研究，以期待找到它们之间一些共性的磁性规律。