基于核K-means与RVM分类回归的Wi-Fi指纹室内定位算法

陈骁，宋安军

（上海海事大学信息工程学院，上海 201306）

Wi-Fi指纹；室内定位；核K-means；RVM；聚类

0 引言

随着互联网以及物联网技术的高速发展，越来越多的新型科技得以服务大众。人们对基于位置服务（Location Based Service，LBS）的需求也趋于广泛化以及多样化。由于全球定位系统（Global Positioning Sys⁃tem，GPS）的局限性以及室内定位需求的增加，室内定位技术越来越引起人们的关注。目前，室内定位技术主要有：ZigBee室内定位、红外室内定位、蓝牙室内定位、超声波室内定位、RFID室内定位、超宽带室内定位和WLAN室内定位等技术。相比较而言，WLAN室内定位由于其无需额外的硬件设备，定位速度较快，总体定位精度较高等特性，得到了广泛的关注与研究应用。WLAN室内定位主要分为两种，其一是基于时间的到达定位技术，主要通过信号接收的时间差，通过算法的计算，获得详细的定位数据。第二种是基于位置指纹的定位技术，该技术通过将接收信号强度（Re⁃ceived Signal Strength，RSS）与物理位置的绑定而进行定位。根据文献[1]所述，基于时间的定位技术，由于受到额外成本或者自身定位精度的限制，无法适用于大量的室内场景。基于Wi-Fi位置指纹的定位技术，主要分为离线与在线两个阶段。离线阶段首先在定位区域内设置若干个距离相等的参考点，在每一个参考节点处测试各个AP的RSS数据，将数据组成n维（n=AP个数）特征向量，再将每个参考点的特征向量存入数据库。这样就如同人类指纹一样，对每一个参考点有各自不同的唯一特征向量，我们把这些数据形成的数据库称为位置指纹数据库。在线阶段，终端设备在参考点覆盖区域内某个位置该点采集RSS数据，再通过与指纹数据库的对比得到定位结果。许多室内定位的研究也引入了SVM方法。但是SVM对于多分类问题的性能不佳，并且需要使用较为准确的超参数来获取更好的性能。文献[2]将KNN算法与SVM融合，使用KNN算法对输入数据进行预处理，再对数据应用SVM算法。但是由于该算法的复杂性等因素，影响定位的实时性。为了提升定位精度与实时性，本文提出了一种融合核K-means与RVM分类回归的室内定位算法。核K-means算法对预处理过的输入RSS特征向量进行无监督聚类，对指纹数据库中的指纹进行区域划分。RVM分类回归算法将终端收集到的RSS数据进行分类，训练出强拟合的回归函数。实验结果表明，该算法相较SVM相关算法，提升了定位效率与定位精度。

1 算法实现

本文算法实现过程如图1，离线阶段通过对建立定位空间中对每个AP的参考点，经过核K-means算法对每个参考点进行聚类，来构建该空间的位置指纹数据库。再使用指纹数据库中的数据训练RVM回归算法，得到数学模型。在线阶段使用RVM分类函数先对在线RSS特征向量进行分类。确定区域后，通过RVM回归函数模型，估算最终的定位坐标。

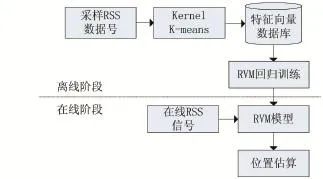
图1 核K-means和RVM分类回归算法的工作流程图

2 核K-means算法的应用

K-means算法是一种无监督的聚类算法，一般是依据欧氏距离的大小来自动聚类的，但只能处理线性可分的数据集。核K-means是在此基础上引入核函数[3]，能够实现非线性可分数据集的聚类。在本文算法的实现中，核K-means算法应用过程如下：

设有参考节点集合P=(p1,p2,p3...pn)，则有n个RSS特征向量rss={rss1,rss2,rss3...,rssi...rssn} ，并建立m个AP（Access Point）的定位模型，则每个参考节点可以收到m个RSS值,其中rssi={rssi1,rssi2,rssi3...rssim}来表示第i个参考点所接收到的各AP信号强度（下标m表示在第i个参考节点处所接收到的第m个AP的RSS值，记为rssim）。用D={D1,D2,D3...Dk}来表示各参考节点所属类别的集合。Kernel k-means算法对参考点聚类的过程基本如下：

①根据K均值算法的取值K，选取K个参考点p的特征向量作为起始均值向量。v={v1,v2,v3...vk}。

②For i=1→m

计算RSS中每一个特征向量与步骤①中选出各均值向量的距离vj（1≤j≤k）的距离，这一步根据文献[2]引入算法的kernel函数，将样本空间中的第i个参考点样本映射到高维空间中。

得出dij（表示当前rssi与均值向量距离最小的类别），再将该参考点归入相应类别中DLi=DLi⋃{rssi}。

End for

③For j=i→k

End if

End for

④重复迭代执行步骤②、③，直到均值向量不再更新为止。由以上的四个步骤，可将获得的数据构造出空间对应的Wi-Fi指纹空间向量数据库。

3 RVM分类回归算法

RVM是2001年Tipping在文献[4]中提出的一种基于贝叶斯框架下的稀疏概率模型。相较于SVM而言RVM可以直接获得后验概率。RVM分类本文中RVM的分类任务，就是判定在线阶段获取的（rssi,yi）数据，属于D中的哪个区域。RVM的分类模型与SVM类似，根据Tipping的文献[1]中所述，相关向量机的模型定义为：

其中K(x,xi)是核函数，ωi是模型权值。在本文中将使用常用的径向基函数（Radial Basis Function，简称RBF）作为核函数，该函数定义：

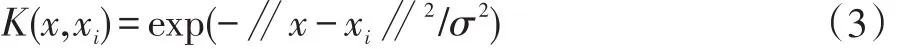
其中σ2表示该核函数的宽度参数。对于核函数的宽度设置非常重要，如果宽度太小，将会导致分类器的过拟合，反之则会造成分类器训练不足。这两种情况都会导致分类的性能受到影响。

其中W=[ω0,ω1,∙∙∙,ωN]T，展开可得：

式中的W和Φ都是大小为N×(N+1)的预先设计的矩阵，并且 Φ=[φ(x1),φ(x2),∙∙∙,φ(xN)]T，其中φ(xn)的值为φ(xn)=[1K(xn,x1)K(xn,x2)∙∙∙K(xn,xN)]T。样本训练过程中随着参数的大量使用，对ωi和σ2进行最大似然估计时，会产生过拟合现象。为了避免产生这种现象，需要对一些参数加入一定的强制附加条件，这种做法在SVM中已有大量十分有效的应用[5]。RVM为每一个权值都定义了高斯先验分布来约束参数，我们引入N+1维超参数α=[α0,α1,…,αN]T，并假设α服从Gamma先验概率分布可得：

再由贝叶斯理论可得：

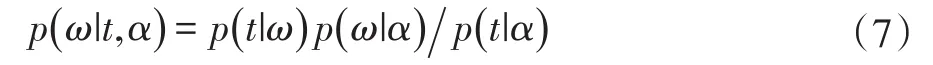
因为p(ω|t,α)与p(t|ω)p(ω|α)成正比，将关于ω的最大后验概率估计等价为最大化：

其 中 ，A=diag(α0,α1,∙∙∙,αN) ，yn=σ{y(xn;ω)} 。又因为p(a|t)与p(t|a)p(a)成正比，求解p(a|t)的问题就可以被转化为超参数的后验分布p(a|t)关于α的最大化问题，可以将p(t|a)最大化：

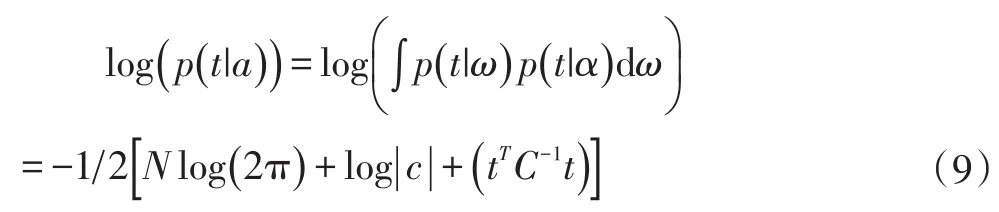
此时再利用拉普拉斯逼近方法不断迭代上两个公式，优化超参数α和参数ω，大部分的ωi最终都将趋近于0，少部分的ωi会趋近于稳定。此时，对应的xi被Tipping称为关联向量（Relevance Vectors），同时模型也完成了稀疏化。

RVM算法由于获得了目标的概率值，在进行二分类的时候，yi需要经过sigmoid函数的处理后，获得样本的类别信息。在室内定位中，RVM模型所遇到的是多分类问题，本文将采用一对一方法将多分类问题分解为二分类问题，这种方法将会产生k（k-1）/2个决策函数。让决策函数对每个分类两两投票，统计所有分类的胜出次数，胜出票数加一，得票最多的那个即最后的预测类。

4 实验场景和结果分析

实验场景如图2所示，在上海海事大学信息与工程学院一楼140大实验室，实验区域总共可以搜索到3个AP热点，数据采集设备为安装有RSS采集软件的小米6手机。（为了展示更为精确的数据，以下实验结果中的数据，不包含无线信号的传输与传播时延。）

图2 实验环境平面图

离线阶段的实验中，将实际的试验区域均匀地布置间隔为1米的参考点，共计25个。每个参考点处采集20次各AP所产生的RSS数据，总共有500个样本作为训练样本，在算法中进行训练。而定位性能的检测阶段，在实验区域内随机选择20个点作为测试点，获取总计400个RSS数据作为测试样本。为了保证模型训练的稳定，以及避免过拟合现象的发生，实验使用10次10折交叉检验法，且尽可能保持数据分布一致。实验中RVM与SVM均选用RBF函数，SVM核参数设置C=8，γ=2，RVM核参数设置为γ=2。其中SVM算法基于 LIBSVM[6]工具箱，RVM算法基于 Tipping的Sparse Bayes程序RVM工具箱[7]。实验中所使用的核K-means与SVM算法，参照文献[8]中的实验方法，最后对比实验数据。

实验结果如图3所示，实验对比了两种算法在本实验条件下的定位误差数据，在相同参数设置下，训练样本为180时，同样经过核K-means算法处理的RSS数据，使用RVM算法的最大误差要小于SVM算法，在1m-2.5m的定位精度中，RVM算法略微低于SVM算法。

图3 不同算法在定位误差中的累计概率分布

如表1所示，两个算法的定位误差图。在训练样本为500时，核k-means-SVM和核k-means-RVM最大误差分别为3.83m、3.53m。最小误差分别为0.49m、0.52m。平均误差分别为1.86m、1.79m。

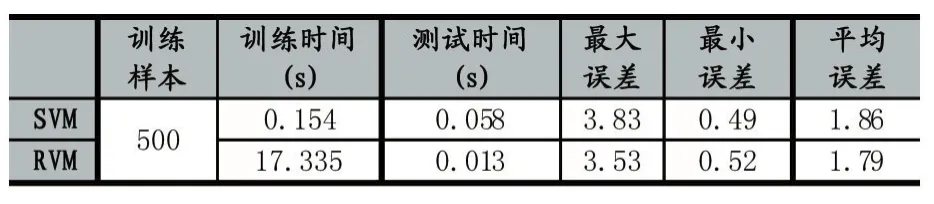
表1 两种算法的各项数据

5 结语

对基于Wi-Fi指纹的室内定位过程中RSS的时效性与定位精度问题，及其衍生的对于指纹数据库的，提出一种基于核k均值与RVM分类回归的定位算法解决方案。在离线阶段，采用核k均值算法对定位参考点进行划分，利用在小区域内进行回归模型的优势提高了对未知数据的泛化能力，并且将相关向量的需求量降低，训练样本个数的需求降低。同时降低了计算复杂度，并且将定位实时性提高。并且省略了SVM算法需要的参数寻优步骤，降低了算法设计成本。实验结果表明，在以1米为间隔布置的参考点和定位区域AP数目稳定的情况下，该算法的测试时间为0.013秒，具有实用价值。