Seismic response analysis of a reinforced concrete continuous bridge considering coupling pounding-friction effect

Lin Yuanzheng Zong Zhouhong Li Yale Wang Liqi

(School of Civil Engineering, Southeast University, Nanjing 210096, China)

Abstract：To evaluate the coupling pounding-friction effect between bridge girders and retainers and its influence on bridge seismic response, a reinforced concrete (RC) continuous bridge is selected as the research object. Three bridge finite element (FE) models were built using OpenSees, in which the longitudinal and transverse pounding elements, as well as the transverse failure element of bearings were introduced. Based on this, the seismic response analysis considering the coupling pounding-friction effect was conducted for the continuous bridge subjected to bi-directional ground motions. Furthermore, the influential parameters were analyzed. The analysis results indicate that the coupling pounding-friction effect can alter the internal force distribution of the bridge structure and generate additional torsional force to bridge columns. The friction coefficient and longitudinal pounding gap size are two important factors. The appropriate friction coefficient and longitudinal pounding gap size can significantly reduce seismic response of girders, and effectively transfer part of the girder inertia force from the fixed columns to the sliding columns, which can reduce the seismic demands of the fixed columns and improve the seismic performance of continuous bridge structures.

Keywords：coupling pounding-friction effect; reinforced concrete continuous bridge; seismic response analysis; bi-directional ground motions; OpenSees

Pounding between bridge superstructures under strong seismic loads is a complex mechanical behavior, which occurs during a tiny period of time involving the phenomenon of local plastic deformation, crashing, friction and energy dissipation between adjacent segments. Previous seismic damage investigations indicated that severe damage of bridge components, unseating of bridge decks and even structural collapse may occur due to the pounding effects[1-2]. Previous research on earthquake-induced structural pounding is mainly based on either the contact-element method or the impact-restitution method. The lumped mass model considering point-to-point pounding is simple and reliable, and it can be adopted for earthquake-induced pounding analysis of bridges[3-5]. Furthermore, some scholars put forward several theoretical solutions to solve the problem of pounding-induced friction between bridge segments. Zhu et al.[6]proposed a three-dimensional contact-friction model to simulate the complicated and arbitrary pounding behavior between bridge girders. Guo et al.[7]presented a modified contact-friction element to simulate the point-to-surface pounding behavior between bridge decks. Zhuo et al.[8]put forward a three-dimensional impact model based on the Kelvin model. Practically, shaking table tests were conducted to investigate the pounding behavior of adjacent bridge segments[9-11]and related numerical simulations were also performed[12-13].

Retainers, also called shear keys, are normally set on both ends of a bent cap to restrain the excessive transverse displacements of bridge girders under transverse seismic loads. The performance of bridge retainers and their seismic responses have been widely studied. Bi and Hao[14]modelled the retainers in bridge structures and revealed their damage modes and influence on bridge seismic response. Deng et al.[15]investigated the pounding effects between girders and retainers of continuous bridges under transverse ground motions and summarized the effects of bridge parameters on seismic pounding responses. Xu and Li[16]did a series of research on retainers and their effects on bridge seismic responses. These studies not only reveal the damage mechanism of bridge retainers, but also provide general guidelines for the aseismic design of them.

The previous studies discussed the longitudinal pounding effects between the bridge segments and the transverse pounding effects between the bridge girder and retainers. Although some of them considered the pounding-friction effect, they only focused on the longitudinal pounding between girder segments. For bridges with transverse retainers, the transverse pounding coupled with longitudinal movement will cause longitudinal friction, and this problem has not been discussed thoroughly yet.

This study evaluates the seismic responses of a reinforced concrete (RC) continuous bridge subjected to bi-directional ground motion excitations considering the coupling pounding-friction effect and figures out its influence on bridge seismic performance. In this study, the advanced FE models considering the pounding-friction effect were built using OpenSees and the seismic responses under bi-directional ground motion excitations were simulated. The influential factors were analyzed and the appropriate advice for aseismic design was proposed.

1 Bridge Models

1.1 Bridge layout

A four-span RC continuous bridge (see Fig.1(a)) is chosen as the research object. The superstructure is a RC continuous box girder and the length of each span is 20 m. The substructures are RC double-column piers. The column height is 4 m and the diameter of column section is 1 m. The bearings on the mid-pier are fixed, while others are longitudinal sliding. The transverse view of the bridge is shown in Fig.1(b). The abutments and the foundations are regarded as fixed boundaries.

(a)

(b)Fig.1 Schematic diagram of the RC continuous bridge (unit: m). (a) General elevation; (b) Transverse view

1.2 Basic FE model

The basic FE model of the continuous bridge is built in OpenSees. The key nonlinear components are columns and bearings. The force-based beam-column element with fiber section is adopted to model the columns and bent caps. The sliding bearings are modelled using the two-node-link element with the elastic perfectly-plastic material, and the fixed bearing is simulated by constraining the translational degrees of freedom. The girder is modelled using the elastic-beam-column element. For bridge columns, Steel02, Concrete02 and Concrete04 are used to simulate the material properties of the longitudinal bars, the cover concrete and the core concrete, respectively. Fig.2 shows the FE model of the bridge. The pounding and friction effects are not considered in the basic FE model.

(a)

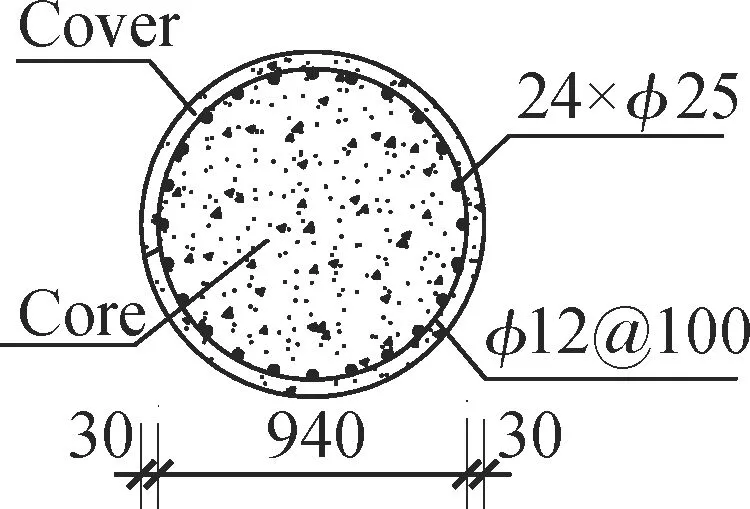
(b)Fig.2 Finite element model in OpenSees (unit: m).

(a) Component tags; (b) Section property of columns

The basic FE model has been validated by a series of hybrid simulations in the previous work[17]. The results of hybrid simulations revealed the basic damage modes of the continuous bridge under seismic excitations; i.e., the damage of plastic hinges in the bottom region of the fixed columns.

1.3 Advanced FE models considering pounding and friction

The pounding and friction effects are considered in the advanced FE models. Based on the basic FE model, tagged as model M1, another two advanced models with different pounding considerations, named models M2 and M3, are built in OpenSees. For model M2, only the transverse coupling pounding-friction effect between girder and transverse retainers is considered, while for model M3, the extra longitudinal pounding effect between girders and abutments is considered. The characteristics of the three different bridge models are shown in Tab.1. The longitudinal and transverse pounding models used in the advanced FE models are shown in Fig.3.

Tab.1 Characteristics of three bridge models

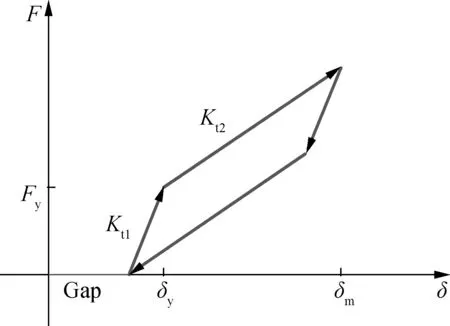
The force-deformation relationship of the longitudinal pounding model adopts the simplified Hertz-damp model which was proposed by Muthukumar[18](see Fig.3(a)). This model uses the bilinear spring model and considers the energy dissipation, whereKt1andKt2represent the initial and the strain hardening stiffness, andδyandδmrepresent the yielding and the maximum penetration displacement, respectively.

The force-deformation relationship of the transverse pounding model refers to the simplified Megally model[19]which was modified by Xu and Li[16]with an extra pounding gap considered (see Fig.3(b)). The strength of the retainer includes both contributions from concrete and rei-nforcements and can be determined according to the shear strength mechanism of the oblique section.Kt1,Kt2andδyhave the similar meanings as the previous model andδnis the deformation corresponding to the ultimate strength.

Since the FE model of the bridge structure is modeled using the beam-type elements, hence, the contact surfaces are condensed to contact nodes. Accordingly, the transverse pounding force can be acquired by the penetration displacement that is determined by the transverse relative displacement according to the idealized pounding model given by Fig.3(b). Meanwhile, the longitudinal friction force on the contact surfaces between the girders and the retainers will be generated when both the following premises are satisfied; i.e., the penetration displacement is non-zero and the longitudinal relative displacement is non-zero. Moreover, the transverse spring elements are considered in the advanced FE models to simulate the transverse failure of bearings before transverse pounding occurs. The key components of the advanced models are drawn in Fig.4. The parameters of pounding elements and the bearing elements are listed in Tabs.2 and 3.

(a)

(b)Fig.3 Pounding models. (a) Longitudinal; (b) Transverse

Tab.2 Parameters of the pounding elements

2 Seismic Response Analysis

2.1 Input ground motions

In total, nine sets of ground motion records are selected

(a)

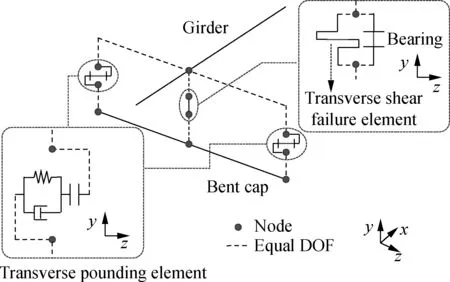
(b)Fig.4 Key components of the advanced FE models. (a) Connections between girders and abutments; (b) Connections between girders and bent caps

DirectionMaterial typeStiffness/(kN·mm-1)Yield displacement/mmEquivalentfrictioncoefficientLongitudinalElastic per-fectly-plastic850.02TransverseElastic per-fectly-plastic4050.1VerticalElastic2 800

from the PEER Ground Motion Database (see Tab.4), and the bi-directional (two horizontal) excitations are considered. The selected ground motion records are uniformly scaled to PGA=0.2gand PGA=0.4gin longitudinal and transverse directions, respectively. A larger transverse ground motion intensity can result in a much more remarkable coupling pounding-friction effect. The excitations are considered to be uniform. The computational time of each case is 40 s with an integration time step of 0.002 s.

2.2 Nonlinear seismic response analysis

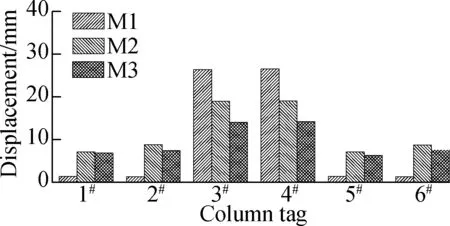
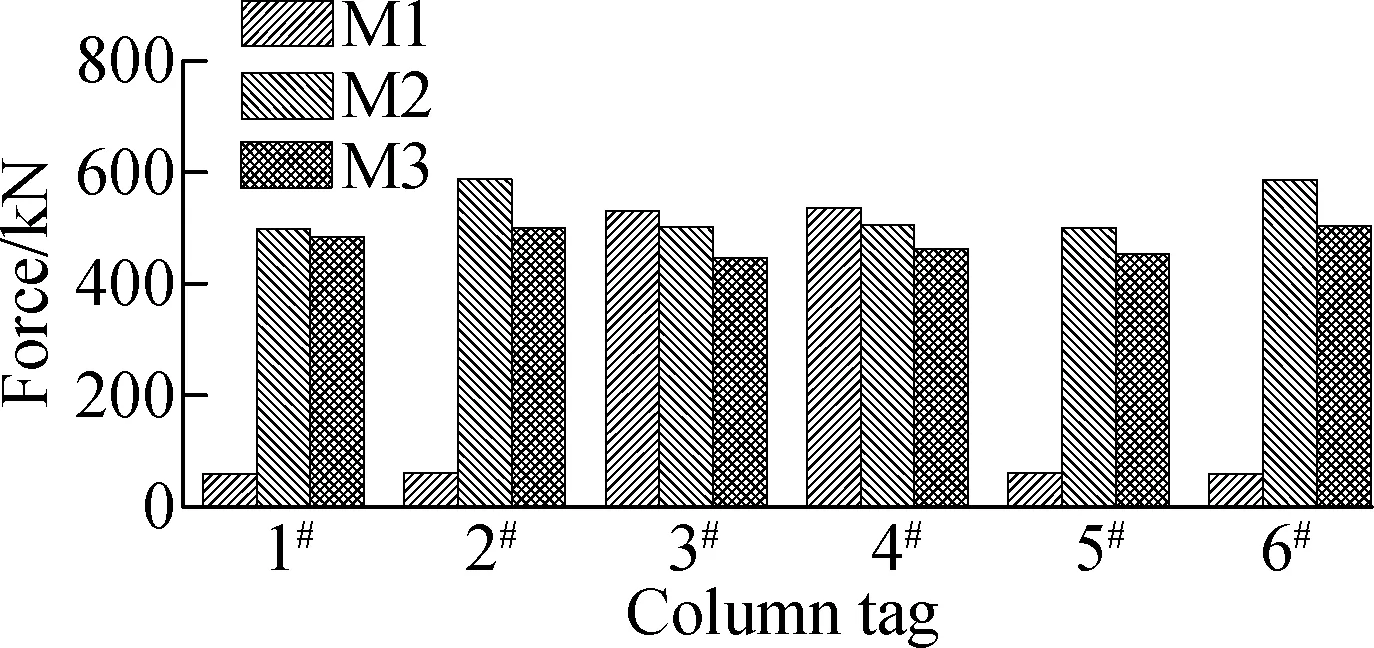
Fig.5 shows the mean values of peak seismic responses of each column to each ground motion excitations. As compared in Figs.5(a) and (b), the longitudinal displacements of the fixed columns (3#and 4#) of model M2 are smaller than that of model M1, while the displacements of the sliding columns (1#, 2#, 5#and 6#)show opposite results. The reason is that the sliding columns of model M1 (basic model) are only subjected to the friction force produced by sliding bearings. However, for model M2 (transverse coupling pounding-friction considered), the sliding columns have to bear the longitudinal friction force when the coupling pounding-friction effect is activated after the bearings are cut off. Compared with model M2, model M3 (extra longitudinal pounding effects considered) shows even fewer deforma-tions in both fixed columns and sliding columns due to the displacement-restriction effect provided by the abutments.

Tab.4 Input ground motions

(a)

(b)

(c)

(d)Fig.5 Column responses to ground motion excitations. (a) Displacement in longitudinal direction; (b) Curvature in longitudinal direction; (c) Shear force in longitudinal direction; (d) Torsional force

The comparison of the shear force of the columns between three models are presented in Fig.5(c). Compared with model M1, the longitudinal shear forces of fixed columns in models M2 and M3 are slightly less, while the longitudinal shear forces of sliding columns reach almost the same level as those of fixed columns (see Fig.5(c)). For further discussion, the internal force distribution pattern is changed, meaning that quite a large amount of girder inertia force originally applied on the fixed columns is transferred to the sliding columns, resulting in fewer deformations in the fixed columns while many more deformations in the sliding columns (see Figs.5(a) and (b)). From the perspective of the entire bridge structure, in total, four sliding columns (1#, 2#, 5#and 6#) can share a great amount of girder inertia force with fixed columns (3#and 4#), which definitely improves the structural internal force response to bi-directional seismic loads. It is worth noting that huge torsional forces are observed in sliding columns in the pounding-considered model (see Fig.5(d)) since the pounding-induced friction forces are applied on one side of the bent caps.

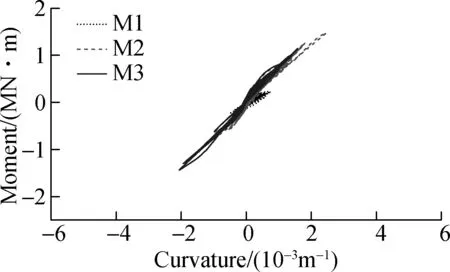
Taking a calculation case for nonlinear analysis, the ground motions recorded at Taft Lincoln School in the 1952 Kern Country earthquake are used in Fig.6. The moment-curvature responses (see Figs.6(a) and (b)) indicate that the sliding columns in model M1 are in elastic stage and the sliding columns in models M2 and M3 slightly enter nonlinear stage. It is noted that the deformations of the sliding columns mainly occur in a single direction for model M2, while the deformations distribute symmetrically for model M3 (see Figs.6(a) and (b)). The longitudinal moment-curvature curves of column 3#in three models are plotted in Fig.6(c), showing different nonlinear levels with different pounding models considered. The girder displacement comparison in longitudinal direction (see Fig.6(d)) indicates the effectiveness of displacement-reduction and displacement-restriction provided by the coupling pounding-friction effect and the longitudinal pounding effect, respectively.

2.3 Analysis of the coupling pounding-friction effect

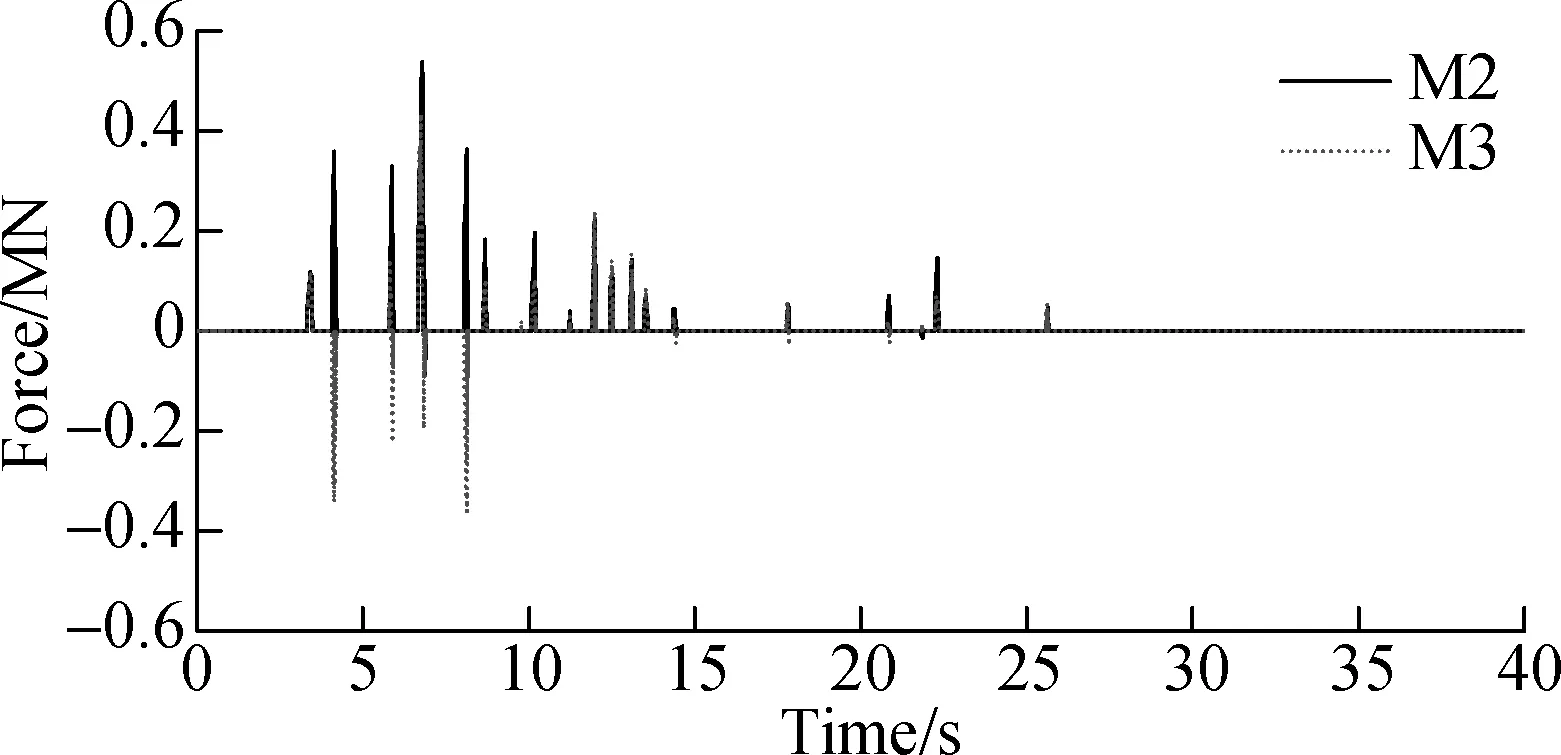
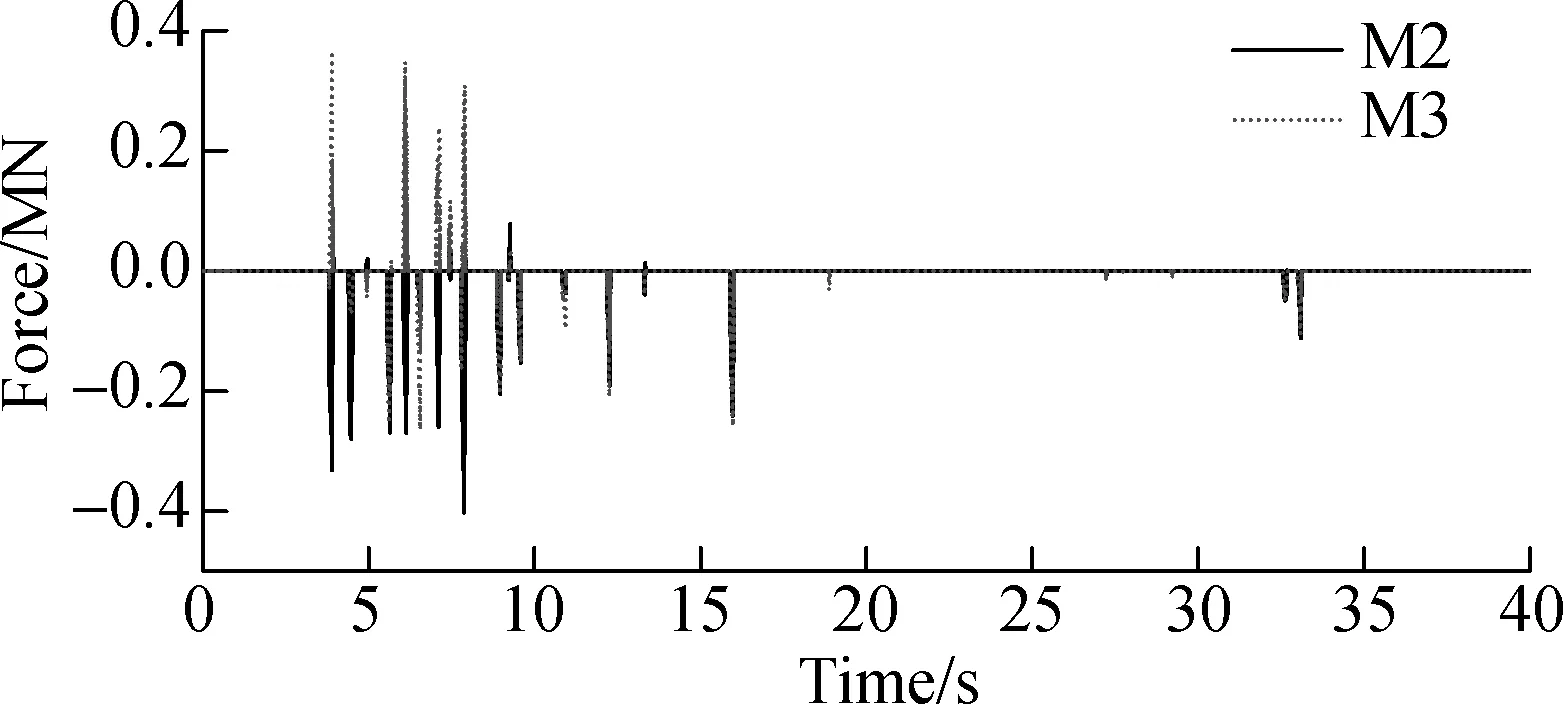
The longitudinal friction forces induced by the transverse pounding of two retainers on bent cap 1#are shown in Figs.7(a) and (b). It is noted that the friction force mainly focuses on a single direction for model M2, while the friction force distributes relatively equally in two directions for model M3. Friction distribution pattern can account for the longitudinal deformation distribution of the sliding columns. Similar phenomena are also observed in other calculation cases. The basic reason can be explained by the girder displacement response to the bi-directional ground motion excitations. As shown in Fig.8, the bi-directional ground motions are excitations for the bridge structure (see Fig.8(a)), causing the girder to move along a circle-like track, i.e., the girder displacement response (see Fig.8(b)). Then, the transverse pounding between girder and retainers occurs (see Fig.8(c)), leading to different pounding-friction patterns for models M2 and M3. The retainers of model M2 experience one-directional friction during the pounding process (see Fig.8(d)), while the retainers of model M3 are subjected to reciprocating friction due to the girder rebounding caused by the longitudinal pounding (see Fig.8(e)).

(a)

(b)

(c)

(d)Fig.6 Nonlinear seismic responses of bridge models M1, M2 and M3. (a) Moment-curvature of column 1#in longitudinal direction; (b) Moment-curvature of column 2#in longitudinal direction; (c) Moment-curvature of column 3#in longitudinal direction; (d) Girder displacement in longitudinal direction

(a)

(b)

(c)

(d)Fig.7 Pounding force and friction force responses of retainers on bent cap 1#of bridge models M2 and M3. (a) Longitudinal friction force of back retainer (-z); (b) Longitudinal friction force of front retainer (+z); (c) Pounding and friction force of model M2; (d) Pounding and friction force of model M3

The transverse pounding force history and the longitudinal friction force history of retainers on bent cap 1#of models M2 and M3 are compared in Figs.7(c) and (d), respectively. The pounding-induced friction takes place simultaneously when pounding occurs. The ratio between the maximum longitudinal friction force and the maximum transverse pounding force can be regarded as a transfer coefficient. For model M2, the transfer coefficient is 0.5 which is the same as the friction coefficient. For model M3, the transfer coefficient is about 0.4 since the longitudinal pounding effect reduces the friction force by the longitudinal restriction of displacement.

(a)

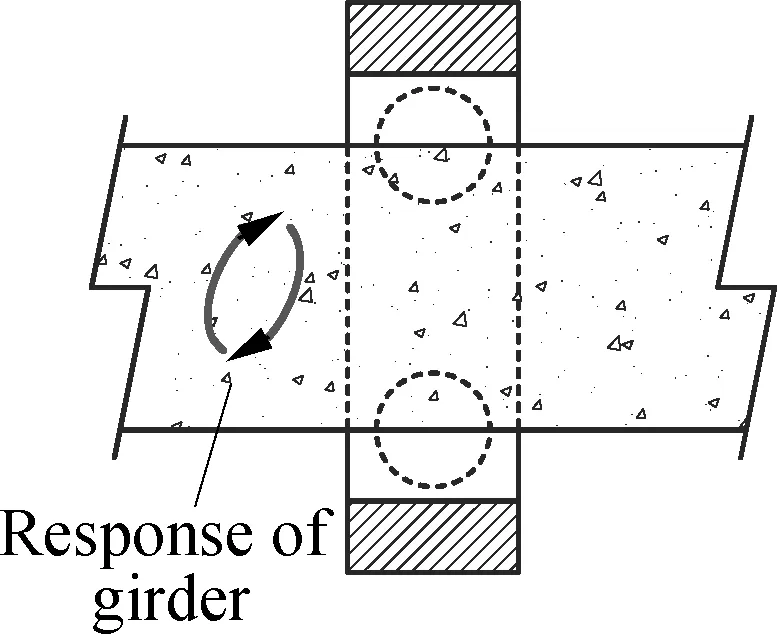
(b)

(c)

(d)

(e)Fig.8 Plan view of pounding-friction process of the bridge models subjected to bi-directional ground motion excitations. (a) Bridge components and excitations; (b) Displacement response of bridge girder; (c) Transverse pounding; (d) Pounding-induced friction without longitudinal restriction of model M2; (e) Pounding-induced friction with longitudinal restriction of model M3

3 Influential Factors

The longitudinal friction force is related to the transverse pounding force and the tangential friction coefficient. Under a particular earthquake intensity, the transverse pounding force is determined and the friction coefficient can be taken as the major factor that influences friction force. The conventional value of the friction coefficient on concrete surface is 0.5 to 0.6, but not limited. According to the Chinese Code for Design of Concrete Structures (GB 50010—2010)[20], the value is 0.8, while other related research[21]recommends 0.4. Previous studies demonstrated that the longitudinal pounding gap size is also an important factor in bridge seismic responses[13]. As has been compared above, the bridge model M3 is obviously more realistic for the further analysis of the coupling pounding-friction effect.

In order to figure out the influential factors of coupling pounding-friction effect on seismic responses of continuous bridge under bi-directional earthquake excitation, a parametric analysis is conducted for two variables, the longitudinal gap size and the friction coefficient between girders and retainers. Model M3 is chosen as the calculation model, and the ground motions recorded at Taft Lincoln School in the 1952 Kern Country earthquake (scaled to 0.2gin longitudinal direction and 0.4gin transverse direction) are chosen as the input excitations. The first situation probes into the effect of the gap size, in which the sizes of longitudinal pounding gap are chosen to be 5, 10, 20, 30 and 40 mm; the transverse pounding gap size is taken as 20 mm; and the friction coefficient is 0.5. The second situation investigates the effect of friction coefficient, where both the longitudinal and transverse pounding gap size are 20 mm, and the friction coefficients are considered to be 0.1, 0.3, 0.5, 0.7 and 0.9. Actually, with the change of two variables, the longitudinal pounding may not take place in some situations, and then the calculation model M3 will be no different from model M2. The real calculation models with different parameters are shown in Tab.5.

3.1 Longitudinal gap size

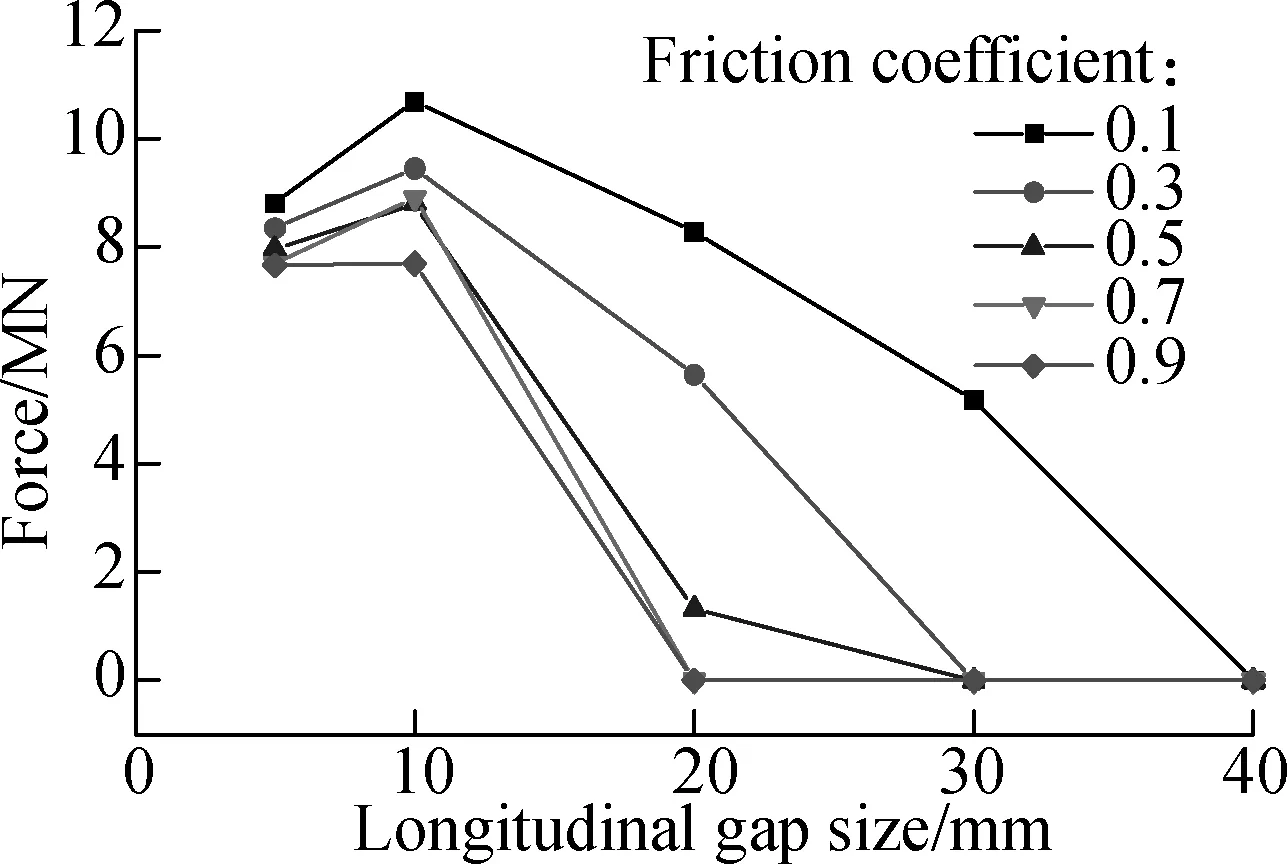
With the increase of the longitudinal gap size, the maximum longitudinal pounding force increases initially, and then decreases after peaking at 10 mm gap size (see Fig.9(a)). It is noted that the longitudinal pounding force will decrease to zero when the gap size is larger than a critical value, meaning that the gap size is sufficiently large and longitudinal pounding is avoided. With the increase of the friction coefficient, the critical value of the gap size decreases. The maximum longitudinal acceleration responses of girder (see Fig.9(b)) show a similar rising and falling trend.

Therefore it can be concluded that for different friction coefficients, there is always a particular critical value in the gap size that determines whether longitudinal pounding will take place or not. When the gap size is larger than the critical value, the calculation model M3 actually turns out to be model M2 with no longitudinal pounding occurring. It is natural that the critical value of the gap size varies with different friction coefficients. However, for a certain gap size, 20 mm for example, the friction coefficient becomes an important factor that influences the longitudinal responses of girder, indicating that a larger friction coefficient will lead to smaller girder responses. If the longitudinal pounding gap size is sufficiently large, the fixed pier may actually fail in advance due to no effective longitudinal displacement constraint. Another conclusion can be drawn that an appropriate gap size under a particular friction coefficient is helpful for the improvement of bridge seismic performance.

(a)

(b)Fig.9 Maximum bridge seismic responses with different longitudinal gap size. (a) Longitudinal pounding force; (b) Longitudinal acceleration responses of girder

3.2 Friction coefficient

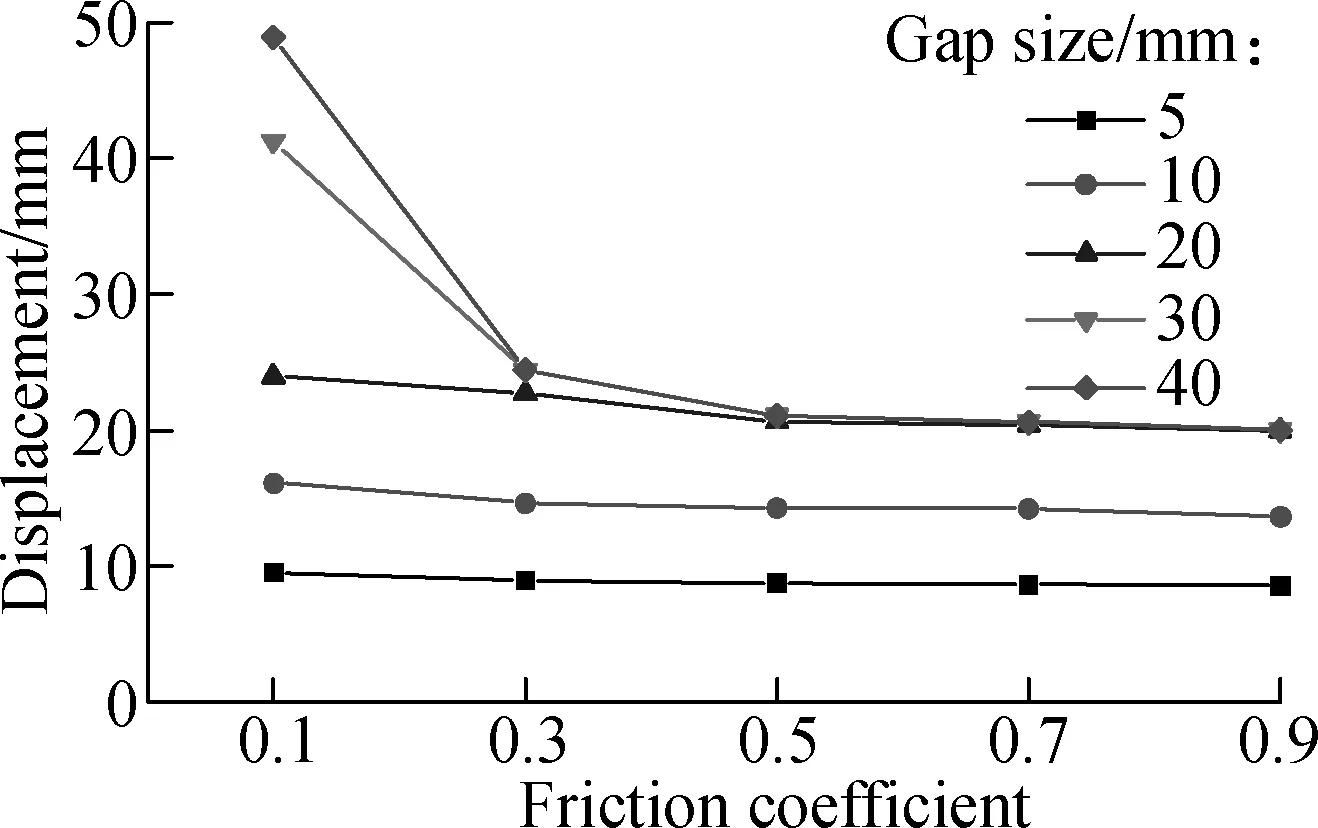
The friction coefficient is an important factor of the coupling pounding-friction effect. Fig.10 shows the variation trend of the maximum bridge seismic response with different friction coefficient values at each level of longitudinal pounding gap size. Column 1#and column 3#are selected to represent the sliding pier and the fixed pier, respectively. The longitudinal displacement of column 1#shows a logarithmic uprising trend with the increase of the friction coefficient (see Fig.10(a)). When the friction coefficient is larger than a certain value, approximately among 0.5 and 0.7, the longitudinal displacement of column 1#will remain at a relatively stable value, meaning that seismic responses of sliding piers are only sensitive to the small value of the friction coefficient.

Also, with the increase of the friction coefficient, the longitudinal displacement of column 3#shows tiny decrease for small gap size, which is less than 20 mm, whereas a sharp decrease at first followed by a stable stage for large gap size, which is more than 20 mm (see Fig.10(b)). Since the fixed pier is rigid with girder, the displacements of column 3#and girder are identical. The longitudinal pounding gap size and the friction coefficient are two influential factors for girder displacement since they provide displacement-restriction effect and displacement-reduction effect, respectively. Then, the displacement variations of column 3#with different friction coefficients at each gap size can be well justified.

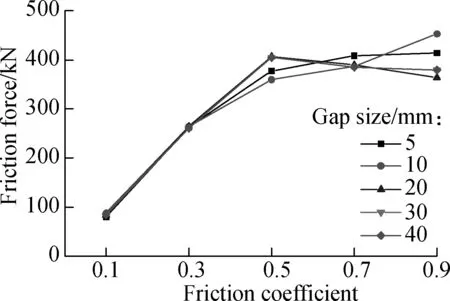
Fig.10(c) gives the maximum friction force of the front retainer on bent cap 1#(+z) with different friction coefficient values at each longitudinal pounding gap size level, and the variation tendency is quite similar to Fig.10(a).

(a)

(b)

(c)

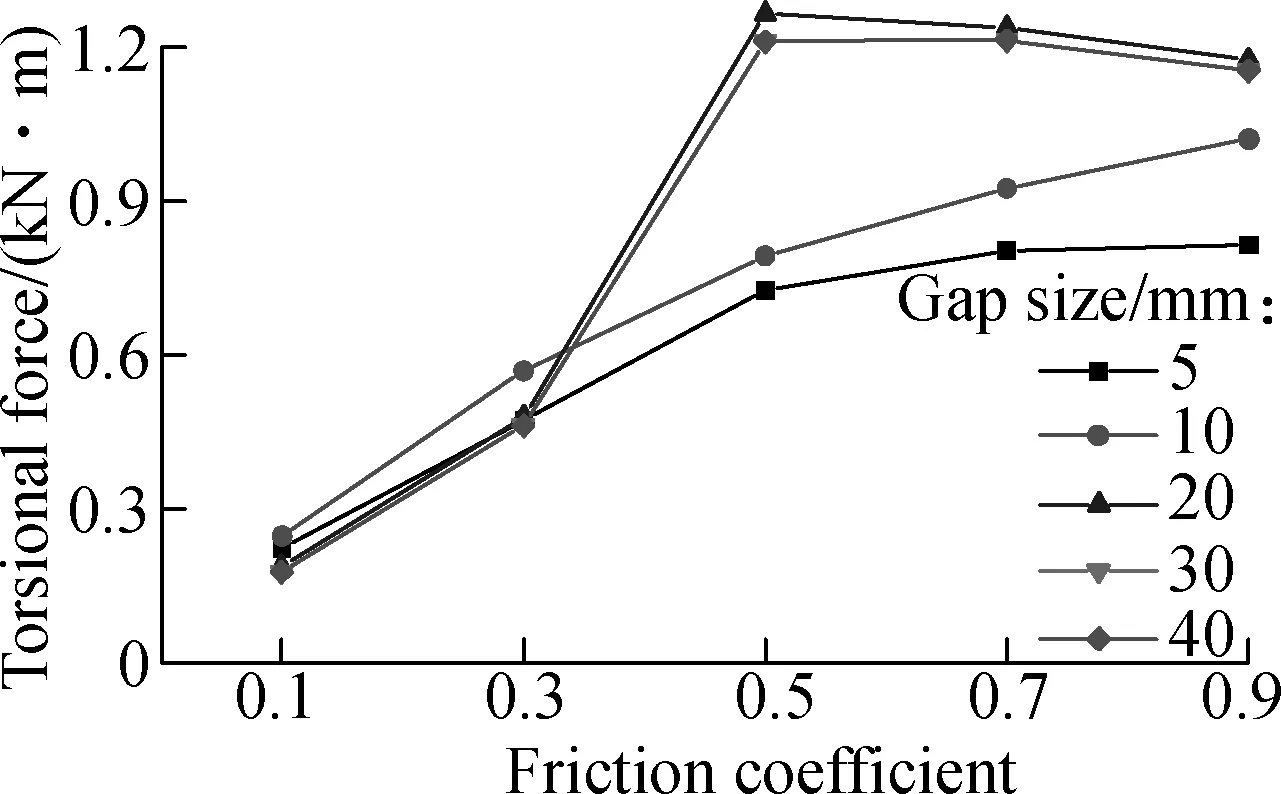
(d)Fig.10 Maximum bridge seismic responses with different friction coefficient. (a) Longitudinal displacement of column 1#; (b) Longitudinal displacement of column 3#; (c) Friction force of front retainer on bent cap 1#(+z); (d) Torsional force of column 1#

The maximum friction force reaches around 400 kN when the friction coefficient is larger than 0.5, almost 60% to 70% of the yield force of a column. Figs.10(a), (b) and (c) validate what has been explained in section 2.3 that part of the girder inertia force is transferred from the fixed columns to the sliding columns when the coupling pounding-friction effect is considered, and further conclude that the larger the friction coefficient is, the more inertia force is transferred.

Torsional forces occur due to the coupling pounding-friction effect. The torsional force of column 1#(see Fig.10(d)) also shows a generally uprising trend with the increase of the friction coefficient. For small gap size cases, the torsional forces increase steadily with the friction coefficient, while for the large gap size cases, the torsional forces actually peak after a sharp rising when the friction coefficient is 0.5, and then become stabilized.

4 Conclusions

1) For continuous bridge with transverse retainers under bi-directional seismic loads, the coupling pounding-friction effect will result in a different structural internal force distribution, which is not commonly considered in general seismic analysis.

2) The friction coefficient and longitudinal pounding gap size are two important factors. Large friction coefficient and appropriate gap size can significantly reduce seismic responses of girder, and effectively transfer part of the inertia from the fixed columns to the sliding columns, reducing seismic demands of the fixed columns and improving seismic performance of the continuous bridge.

3) Rough surfaces of the retainers are recommended in order to acquire a large friction coefficient. Also, for the longitudinal pounding gap size, there should be a relatively large value for the condition of avoiding bending failure of the fixed columns in advance.

4) Uncertainties exist for seismic response analysis of bridges under bi-directional strong earthquake excitation considering the coupling pounding-friction effect. This study summarizes the mechanism of the coupling pounding-friction effect and some qualitative laws in a much more idealized case. Further verifications in practical cases are needed.