基于用户签到行为的群组兴趣点推荐模型

陶永才，丁 鑫，石 磊，卫 琳

1(郑州大学 信息工程学院, 郑州 450001)

2(郑州大学 软件技术学院, 郑州 450002)

1 引 言

近年来，互联网的发展促使人们从信息匮乏的时代进入信息过载的时代[1].推荐系统通过挖掘用户与项目之间的关系，分析用户的兴趣分布，帮助用户从海量数据中发现符合其兴趣的项目，满足用户的个性化需求[2].

随着基于位置的社交网络的快速发展，为用户推荐其可能感兴趣的地点成为一个研究热点.现有的推荐系统主要关注如何为单个用户提供个性化推荐服务，而在实际生活中人们通常是以群组的形式参加各种活动，因此推荐系统更需要考虑如何向群组推荐，使推荐结果能够满足群组的需求并使所有群组成员都均衡满意.除了要准确获取组内成员的个体偏好外，群组推荐系统还需要考虑如何将多位组员的个体偏好融合为群组偏好[2]，因此偏好融合策略，成为群组推荐研究的关键.现有的偏好融合策略都有各自的优点和不足，例如均值策略[3]在组内成员偏好非常相似时得到的聚合效果较好，但如果组内成员的喜好差别很大，那么结果将变得较差.最开心策略将群组成员中的最高评分做为群组评分，但易产生"痛苦"问题.最小痛苦策略能避免"痛苦"问题，但无法解决恶意评分的问题.基于此，本文在GPUC模型中使用一种加权混合融合策略以弥补单一融合策略的不足.考虑到不同的用户对群组偏好的影响不同，在进行偏好融合时应该为用户分配不同的权重，GPUC模型根据用户的活跃度来分配权重.然后根据群组偏好的差异度选择不同的融合策略.与文献[5]提出的HAaB算法的对比实验表明，采用了加权混合融合策略的GPUC模型推荐准确度提高了4.03%.

2 相关工作

2.1 推荐算法

目前常用的推荐算法有基于邻域的算法，隐语义模型，基于图的模型，混合推荐算法等.基于邻域的算法包括基于用户的协同过滤算法和基于内容的协同过滤算法.基于用户的协同过滤算法根据用户评分比较用户间的相似性，并向目标用户推荐相似用户感兴趣的项目[16].基于内容的协同过滤算法是从待推荐对象中选择与用户已经选择的对象有相似特征的项目做为推荐结果[17].隐语义模型是一种基于机器学习的方法，通过优化特定的指标建立最优的模型.找到用户兴趣和项目之间的隐含特征联系.具有较好的理论基础.推荐系统中常用的模型和方法有LDA模型，隐含类别模型，矩阵分解等.基于图的模型将用户和项目的二元关系抽象为图，将用户和项目抽象为图中的点，用户对项目的行为抽象为边，利用图上的算法进行推荐.混合推荐算法是为了弥补单个推荐算法的不足综合上述方法中的两种或更多来进行推荐.例如文献[14]提出的HLB混合推荐算法针对用户的长短期兴趣的差异，对用户的长期阅读兴趣采用基于内容的协同过滤推荐算法，短期阅读兴趣则采用基于用户的协同过滤推荐算法[14].

2.2 群组推荐的偏好融合

在进行群组偏好融合时要考虑使用哪种偏好融合方法和融合策略.

群组推荐的偏好融合方法根据融合发生的阶段分为：模型融合和推荐融合.模型融合发生在推荐形成之前，首先将群组成员个体偏好模型融合形成群组偏好模型，然后基于群组偏好模型为群组进行推荐.推荐融合则是在组内成员个人推荐生成后，将所有成员的推荐结果根据一定的融合策略进行融合得到群组推荐结果.电影组推荐系统HappyMovie[10]，音乐组推荐系统MusicFX[8]均采用推荐融合方法，而旅游组推荐系统CATS[9]则采用模型融合方法.目前对于具体应该采用哪种偏好融合方法并没有统一的定论.偏好融合方法的选择往往是根据实际情况得出的.文献[13]提出"群组偏好与个人偏好具有相似性"，并利用该结论提出一种改进的偏好融合组推荐方法，将模型融合和推荐融合统一.偏好融合策略则是指将单个组员的个体偏好融合为群组偏好的方法.在实际应用中，为了满足满意度、公平性和可理解性等要求，常常会根据不同的情境选择不同的融合策略.常用的组推荐融合策略有公平策略、均值策略、痛苦避免均值策略、最小痛苦策略、最开心策略.文献[11]对经典常用的偏好融合策略进行了研究讨论.分析了上述策略的优点和不足之处，例如最开心策略可能会引起个别群组成员的不满，产生所谓的"痛苦"问题；痛苦均值避免策略解决了"痛苦"问题，但其融合策略与阈值的选择有很大关系.

2.3 群组推荐的研究现状

群组推荐正受到越来越多的关注.ACM推荐系统大会在2011年以"家庭群组电影推荐"为主题举办了推荐挑战赛[7].旅游组推荐系统CATS[9]、音乐组推荐系统MusicFX[8]是目前存在的典型商业组推荐系统.群组推荐一般包括两个步骤：一是融合组内成员偏好形成群组偏好；二是根据群组偏好对项目进行预测并生成推荐列表.Fernando Ortega等的研究表明组推荐系统的性能根据群组的大小有所不同，而基于矩阵分解和协同过滤技术的组推荐系统在其实验数据集上表现最好[4].文献[6]采用模型融合的方法，基于用户的社交网络关系构建群体偏好模型为群组用户进行视频推荐，取得了较好的推荐效果.文献[12]在SVD中加入用户的社交行为和社交关注关系特征，将其用于个体推荐并通过对个体推荐列表的融合获取群组推荐.文献[5]则假定推荐列表是根据用户评分排列，提出一种列表融合方法HAaB，将均值策略和波达计数结合使用，得到了较好的推荐效果.

3 基于用户签到行为的群组兴趣点推荐模型

由于推荐融合的方法具有更高的灵活度且推荐结果更易于解释，GPUC模型采用推荐融合的方法，首先为组内成员进行个体推荐，然后根据加权融合策略融合组员的推荐列表.在进行融合时要考虑到不同组员对群组偏好的影响也不同，例如比较活跃的用户对群组偏好的影响应该比不活跃的用户影响大，因此应为不同的用户分配不同的权重，同时为了弥补传统偏好融合策略的不足，本文采用一种混合融合策略，根据组内成员偏好的差异度采用不同的融合策略.

图1为GPUC模型推荐过程的流程图.

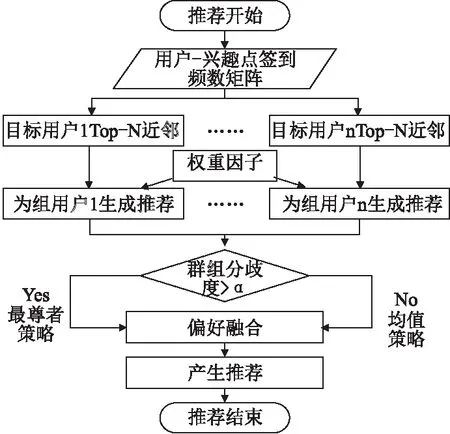
图1 推荐流程示意图Fig.1 Recommended flow diagram

1)抓取用户数据，形成用户-兴趣点签到频数矩阵.

2)将矩阵向量化，找到与目标用户有相似兴趣的最近邻集合，通过基于用户的协同过滤为目标用户推荐其可能感兴趣的项目.基于TF-IDF的思想预测用户对推荐项目的评分.从而得到用户个人推荐列表.

3)通过用户-兴趣点签到矩阵计算用户的权重，同时根据用户个人推荐列表生成群组-推荐地点评分矩阵.根据群组评分的分歧度选取合适的融合策略融合组内成员偏好，并将融合后得分最高的地点推荐给用户.

3.1 个人推荐列表

1)获取用户-兴趣点频数矩阵

为用户进行推荐首先要获取用户的偏好，进行组推荐则首先要获取组内所有成员的偏好.一般的用户偏好获取方法分为显式获取和隐式获取.显式获取模式根据用户对项目的评分获取用户偏好.但现实中很难要求用户对每一个项目都进行评分，因此显式获取的方式易出现稀疏性问题.隐式获取模式则不需要用户提供偏好信息，而是根据用户的历史行为来挖掘用户偏好.采用隐式获取用户兴趣的方法更有利于保护用户的隐私.因此本文采用隐式获取的方法，提取用户的历史签到记录，得到以下的用户-兴趣点签到频数矩阵.

(1)

其中m表示数据集中的用户数，n表示数据集中有用户签到的兴趣点的总数.Vi,j表示第i位用户在兴趣点j处签到的次数.

2)最近邻集合

两个用户签到地点越相似则这两位用户的兴趣分布越相似.矩阵中每一行代表一个用户的兴趣分布，可以表示为向量形式，例如Vi={vi,1,vi,2,…,vi,n-1,vi,n}表示用户i的兴趣分布，则两位用户之间的相似度计算如式(2)所示.

(2)

其中sim(ui,uj)表示用户i和用户j(i,j=1,2,…,m)之间的相似度.将用户按照和目标用户i的相似程度排序，取前K位用户组成用户i的最近邻集合Ni.将K位最近邻签过到的兴趣点做为目标用户的待推荐项目.

3)评分预测

基于用户的签到信息只能获取用户的兴趣点和签到频次，无法得到用户对兴趣点的评分.TF-IDF是一种评价字词对文件重要程度的算法，该算法在考虑字词重要性的同时也兼顾了字词的普遍性[15].在预测用户对兴趣点的喜好程度时可以借用TF-IDF算法思想：用户在某一地点签到次数越多，说明用户对该地点更感兴趣，但若数据集中的用户在该地点签到频数较高则说明对该地点的推荐缺乏新颖性，使用TF-IDF来计算用户对某一兴趣点的喜好程度如式(3)所示.

(3)

其中deg(ui,pa)表示用户i对兴趣点a的喜好程度.n(i,a)表示用户i在兴趣点a处签到的次数，num(i)表示用户i签到总数，Tu表示数据集中用户的总数，Nu(a)表示在地点a签过到的用户数. 对于用户i签过到的兴趣点可以使用公式(4)得到一个0到1之间的数字做为用户i对兴趣点a的评分.

(4)

其中deg(ui,p)表示用户i对所有兴趣点的平均喜好程度，rat(ui,pa)表示用户i对兴趣点a的评分.

公式(4)可以用于为用户签过到的兴趣点评分，对于用户未签到的地点则使用协同过滤的方法，根据在该地签过到的最近邻用户的评分生成预测评分.如果最近邻用户j对兴趣点a的评分为rat(uj,pa)，则目标用户对该地点的评分如式(5)所示.

(5)

对组内用户推荐过程如算法1所示：

算法1.组内用户个体推荐算法

输入：matrix，数据集上用户-兴趣点签到频次矩阵；

G，待推荐组用户集合；

N，计划推荐给用户的项目数；

输出：每个组内用户的推荐列表.

1.foreach useruiin G

2.calculate similarity betweenuianduj

//利用公式(1)计算两用户间的相似度

3. make the first kth users as neighbors[]

4.foreach neighbor in neighbors[]

5.forpain neighbor′s sign-in collection

6. calculate deg(neighbor，pa)

//利用公式(3)

7.if(uihas been signed inpa)

8. rat[a]=rat(ui,pa);

//已签到地利用公式(4)

9.else

10. rat[a]=rat(ui,pa);

//未签到地利用公式(5)

11.endif;

12.endfor;

13.endfor

14.sort the rat[] in descending order;

15.while(count!= N){

16.recommend_list[count++]=pj}

17.}

18.end

3.2 偏好融合策略

传统的偏好融合策略忽略了不同的群组成员对群组偏好的影响，在一个群组中，由于每位成员的活跃度不同，对群组偏好的影响也不同，在进行偏好融合时，活跃度高的用户的偏好更具有参考价值.基于此，本文考虑根据用户的活跃度来计算用户在群组中的权重，而用户在不同的地方签到次数越多则说明用户越活跃，该用户对群组兴趣的影响越大.设计权重的计算如式(6)所示：

(6)

其中w(ui)表示用户i在群组中的权重.fi表示用户i签到总次数，qi表示用户i成为其他用户近邻的次数，由公式(6)可以看出随着fi，qi的增加，用户权重也呈现增长趋势.对两个参数进行调和则可以全面反应用户在群组中的权重，对公式(6)进行化简，得到最终权重公式如式(7)所示.

(7)

融合策略的效果与组内成员偏好差距有关，例如当组内成员偏好差距较小时，均值策略的效果会比较好，但当成员偏好差别较大时均值策略会对评分较少的群组成员产生不公平现象.本文考虑组内成员偏好的差异度同时结合用户在组内的权重.当群组成员对一个项目的评分差异较小时，采用加权均值策略，取群组成员对该项目的加权平均分做为群组评分.当群组成员对一个项目的评分差异较大时采用最尊者策略，权重最大的组员即为最尊者，将最尊者的评分作为群组评分.加权混合融合策略的评分计算如式(8)所示.

(8)

其中rat(ui,pa)表示用户i对推荐地点a的评分，diff(pa)表示群组用户对待推荐地点a评分的分歧程度.分歧方差计算如式(9)所示.

(9)

其中ave(G,pa)是群组中的用户对待推荐地点a预测评分的平均值.

基于加权混合融合策略的群组推荐过程如算法2所示：

算法2.群组推荐算法

输入：matrix，数据集上用户-签到频数矩阵；

Vi，群组用户-推荐集合评分矩阵；

G, 组用户集合；

输出：群组推荐结果.

1.foreach useruiin G

2. calculate weight w(ui)

3.endfor

4.foreachpainvi

5. if(diff(pa)>α)

6. for(i in G)

7. {

8. if(w(i) is the most weighted)

9. GR[j]=rat(ui,pa)

10. }

11. else if(diff(pa)<α)

12. GR[j]=average(G,pj)

13.endfor

14.sort the GR[j] in descending order;

15.make the GR[0] as recommendation result

16.end

4 实 验

4.1 实验数据集

Gowalla是著名的基于位置的社交网络站点，为用户提供了基于位置的签到服务，本文采用的数据集1是由斯坦福大学的研究学者通过Gowalla网站的公共接口获取的.数据集共包含两个文件，分别记录签到信息和用户关系信息，均以txt文件格式存放.签到记录中共收集了6442890个签到记录，每个基本数据项包含用户ID、签到时间、签到经纬度、签到地点ID等数据项.在选择用户组时首先将两份文件导入数据库并利用用户ID将两表连接，过滤掉签到频数过低或朋友关系过少的用户.最后将数据集按照8：2的比例划分为训练集和测试集.

4.2 算法评价标准

基于用户签到行为的群组兴趣点推荐分为个体推荐和群组推荐两步.

准确率和召回率是TOP-N推荐的重要评价标准.在兴趣点的推荐中，准确率表示在推荐给用户的项目中，用户签到的地点数占推荐数量的比例.召回率是用户签到的兴趣点中被推荐地点所占的比率.F值是准确率和召回率的调和平均值.本文利用F值来度量个体推荐结果的精确度.对于用户u，令Ru作为模型推荐的地点集合,Tu作为测试集中用户u签到的地点的集合,其推荐准确率P、召回率R、以及F值的计算分别为:

(10)

(11)

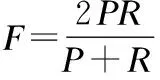
(12)

而群组通常是由多个个体组成的，一位成员的选择不能代表群组的选择，因此上述评价标准不适用于对群组推荐效果的评价.而RMSE(平方根误差)通过计算预测评分与真实评分之间的误差来评价推荐系统的推荐效果.本文将RMSE改进后做为群组推荐结果的评价标准.群组推荐评价标准RMSE计算公式如式(13)所示.

(13)

其中r(ui,pa)表示用户i对推荐地点a的评分,G(pa)表示群组G对推荐地点a的评分.N表示该组用户在推荐地点a签到总次数，Gn代表群组成员个数.

4.3 实验方案

实验设置情况如下：

1) 比较不同的相似邻居个数k的值对个体推荐准确率的影响.

2) 调整差异度阈值α使推荐效果达到最优.

3) 将加权混合融合策略的推荐效果与其它融合策略的推荐效果进行比较.

4.3.1 相似邻居个数

为了使群组推荐效果达到最优，要尽可能准确的获取组内成员的个人偏好.而对个体用户进行协同过滤推荐时，相似的邻居个数k的值对推荐结果有一定的影响，实验对比了不同的k值对个体推荐结果准确率的影响.结果如图2所示.由图2可以看出在实验数据集上，当邻居个数k的值为15，推荐个数为20时，推荐的准确率最高.

4.3.2 差异度阈值α

差异度阈值α影响着融合策略的选择，实验以7人群组为推荐对象，每次实验分别设置不同的α值，对推荐结果进行评价，实验结果如表1所示.由表1可以看出当差异度阈值取0.4时，推荐精度更高.

1http://snap.standford.edu/data/loc-gowalla.html

图2 用户邻居数对个人推荐准确率的影响Fig.2 Precision of different numbers of neighbors

表1 不同差异度阈值α的实验结果表Table 1 Result of different threshold α

为了得到本文提出的加权混合融合策略的最佳条件，反复调整群组规模和差异度阈值α，实验结果如图3所示.由图3可以看出根据群组大小不同，α的取值也应该有所不同，在群组人数较少时，α取较小的值可以提高推荐质量，而当群组规模较大时，阈值α也应该适当增大.实验结果表明在Gowalla数据集上，当目标群组人数为7，差异度阈值α取0.4时，推荐效果最好.

图3 不同群组人数及α值的推荐结果Fig.3 Result in different group size and threshold α

4.3.3 加权混合融合策略和其他融合策略的比较

为了验证GPUC模型中采用的加权混合融合策略的有效性，实验选择和传统的单一融合策略平均满意度策略，最尊者策略以及文献[5]中提出的HAaB策略进行比较.由于HAaB策略在群组成员偏好相似度较高的情况下推荐效果较好，而加权混合融合策略通过差异度阈值α的调和，对群组差异度不敏感，推荐准确度相对稳定.为了验证该策略在不同群组中的有效性，实验设置两组由7名用户组成的群组做为目标群组.其中一组为偏好相似度较高的群组，由随机挑选的一位目标用户及其最近邻集合中的前6位组合而成.另一组则为低相似群组，由随机挑选的7名用户组成，在挑选的过程中将互为最近邻的用户去掉，直到群组中没有互为最近邻的用户为止.在使用GPUC模型推荐时，将差异度阈值α设为0.4.实验结果如图4所示.由图4可以看出，平均满意度策略，最尊者策略以及HAaB策略的推荐效果与群组偏好相似度的大小关系较大，对偏好相似度较高、偏好差异较小的群组的推荐效果要优于相似度较低的群组.而无论群组差异度大小，GPUC模型通过差异度阈值α的调和使得模型可以根据具体情况选择具体的融合策略，充分发挥各个融合策略的优势，因此对群组偏好差异度大小不敏感，推荐效果只与群组人数及差异度阈值α的选则有关，保证了模型在群组偏好相似度较高或者较低时都有较好的推荐效果，在对偏好差异较大的群组进行推荐的准确度交HAaB提高了4.03%，对偏好差异较小的群组进行推荐的准确度提高了1.31%.

图4 不同融合策略的实验结果Fig.4 Results in different aggregation strategies

5 总结与展望

由于人类的社会性，群组推荐逐渐成为了推荐系统的研究热点.本文提出了基于用户签到行为的群组兴趣点推荐模型GPUC.模型中采用了加权混合偏好融合策略融合群组成员的个人偏好，该策略既考虑了不同用户对群组偏好的影响，同时也弥补了传统的单一融合策略的不足，通过差异度阈值α的调和使GPUC模型在相似度较高的群组和相似度较低的群组中都有较好的推荐效果.相较与传统的单一融合策略以及HAaB，本文提出的偏好融合策略能为用户产生更准确的推荐.