考虑碳排放的贵州省茶叶物流配送路径优化设计
2018-10-17XUELiangZHENGYanYUWei
薛 亮,郑 琰,余 伟 XUE Liang,ZHENG Yan,YU Wei
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
(College of Automobile and Traffic Engineering,Nanjing Forestry University,Nanjing 210037,China)
0 引 言
中国是茶叶生产及销售大国,拥有世界第一的茶园面积的天然优势,而中国的茶叶出口量却是第二,与第一名有着较大的差距,除了由于自身对于茶叶的大量消费因素外,物流因素也是制约中国茶叶向外扩张的原因之一。
贵州省作为中国茶叶大省,拥有着得天独厚的茶叶生产基础。据相关调研可以知道,贵州茶叶出口存在很大上升空间[1],要让贵州省茶叶走出去,需要做好茶叶的物流工作,只有做好物流配送,才能促进商品的流通。本文对物流配送路径以碳排放为主要参考指标,综合考虑了车辆载重、车辆油耗等因素建模分析。
1 物流配送路径优化建模
1.1 问题假设
在车辆载重量一定的条件下,主要研究讨论以下几种成本:车辆使用的固定成本、车辆运输过程中的运输成本以及碳排放的成本。建立数学模型,从数字的角度考虑这些成本之和最小[2]。
假设如下:
(1)车辆从某省市内的某茶叶物流配送中心出发;
(2)有且只有一个物流配送中心;
(3)车辆实时载重量不能超过该车的最大载重量;
(4)每个需求点的需求和距离已知;
(5)目标达到碳排放和运输成本的总体最优。
1.2 碳排放计算公式
针对路径全过程中的碳排放,主要考虑的是运输和配送过程中使用石油、柴油等化石燃料后排放出的二氧化碳,因此为确保计算准确性,在计算碳排放前一般需要建立质量平衡方程式,从而确保物质的输入、积累以及输出达到平衡。从而计算产品各个阶段的碳排放,基本公式为:
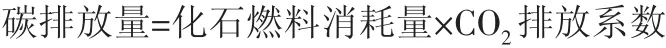
燃料消耗的多少和距离的远近有着直接联系,行驶距离越远,燃料消耗越多,但与此同时还与车辆当时的载重量有着必然的联系。可以笼统将单位距离的化石燃料消耗量P与车辆装载量q的关系理解为一个简单的线性函数:
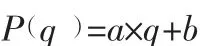
其中:a:装载量与化石燃料消耗量关系的系数;b:固定值,为车辆使用固有消耗的碳排放量。
那么,车辆在配送(i,j)区间产生的碳排放成本为:
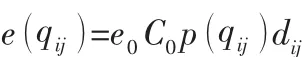
其中:e0为CO2的排放系数;C0为单位二氧化碳的排放成本;p(qij)为(i,j)路段上单位距离车辆化石燃料的消耗量;dij为两需求点(i,j)之间的距离。
1.3 车辆运输成本计算
在本模型中,本文考虑了两部分,运输成本和固定成本。运输成本是指完成此次运输可能产生的费用,它与单次运输的距离长短,单位运输产生的成本有着直接的关系,在这里简单的将运输成本考虑为单位成本×距离;而固定成本表示的是成本不随业务量的增加而产生变化的成本,在车辆运输中,将人工成本、车辆折旧费用等考虑为固定成本,计作O0,因而可以得到运输成本计算公式:

其中:Lij为两需求点(i,j)之间所耗用的运输成本;h0为运输成本系数,即单位距离需要的成本;dij为两需求点(i,j)之间的距离;O0为固定成本,一辆车只计算一次。
1.4 模型参数与变量设定
N=[1,2 ,…,n]表示需要配送的需求点的集合;qi为第i个需求点的需求量,同时0≤qi≤q;dij为第i个需求点到第j个需求点的距离;h0为车辆的单位运输成本O0,车辆的固定成本;e0为CO2的排放系数;C0为单位二氧化碳的排放成本;p(q)为单位距离车辆化石燃料的消耗量(在线性函数中,a代表单位距离内车辆每增减1kg货物需要额外消耗化石燃料的系数,b代表车辆单位距离内固定消耗的化石燃料量);k为单位油耗的价格。
1.5 数学模型
在模型中,i=0是指茶叶物流配送中心,当i=0时,d0=0,则考虑碳排放的配送数学模型如下:
目标函数:
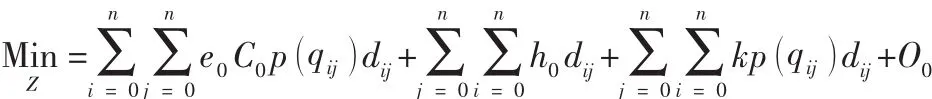
目标函数在要求总成本最小的情况下,考虑了碳排放成本、运输成本、油耗成本以及车辆使用的固定成本。
在上述模型中,目标函数由四部分组成:
O0,车辆使用的固定成本。
1.6 蚂蚁算法设计
蚂蚁算法的核心思路是从蚂蚁在觅食等过程中依赖信息素进行信息传递,当其他蚂蚁接受到浓度强的信息素时就会选择这条道路,越来越多的蚂蚁走在同一条路径上时,散发的信息素浓度就越强,则后续蚂蚁选择这条路径的可能性就越大。当更多的蚂蚁聚集在一条路径时,则说明该路径是此问题的最优求解[3]。
初始路线的选择不会影响到蚂蚁算法的最终结果,同时它也不需要对搜索结果进行人工的干预调整。蚂蚁算法的最终解不取决于初始路线的选择,并且不需要手动调整搜索解的过程。在较少的参数条件下,蚂蚁算法就能获取组合的优化结果。
本文利用蚂蚁算法求解VRP的具体过程如下:
(1)输入物流配送数据和参数,计算第一个全局解。
(2)设开始时间t=0,迭代次数Nc=0。在物流配送中心有m只蚂蚁,然后建立蚁群禁忌表。
(3)对每个蚂蚁i,遍历节点列表,寻找出没有经过的节点,利用概率转移公式为蚂蚁挑选将要经过的下一个客户节点j。
(4)计算运输货物的总量q和路径(i,j),用Q表示每辆车的最大载重量,如若q>0,则进入步骤(5),否则将节点j加入可行的点集合A中,并跳转进入(6)。
(5)把点j加入禁忌表中,同时把点i到节点j的路径长度放入(3),否则将节点j重新加入可行点集A之中,进入下一步 (6)。
(6)统计车辆数,并对可行点集合A进行遍历判断,如果A为空,则进入步骤(7),否则,从A中挑出没有被搜索的节点,并选择开始时间最短的节点为起点,返回步骤(3),搜索下一个节点。
(7)更新局部的信息素及受影响的信息增量。
(8)对k只蚂蚁的最短路径长度和最短路径进行搜索,同时计算最少费用以及相应的最少费用路径,并更新路径上的信息素,开始循环时,如果所有蚂蚁均巡游一遍,那么对k只蚂蚁搜索过的边信息素进行更新,否则更新本次循环的最优路径。
(9)比较本次运算的结果与之前得出的最优化结果,若本次运算的结果优于之前得到的最优解,则进行数据更新,将本次运算结果替代前次最优化结果,成为新的最优化结果。
(10)若所有运算均已完成或已计算出最优化结果,运算完成,否则,将禁忌表清零,返回步骤(2),重复上述步骤。
2 实例分析
2.1 配送数据及模型参数
本文以贵州省都匀市内某茶叶贸易有限公司,从其物流中心出发,该公司向上海地区输送,沿途对一些地区的需求点进行供货,继而进行相关案例分析。这些需求点具体有长沙、无锡、常州、南京、南通、宣城、盐城、昆山、上海。
物流配送中心编号为“AO”,对分布在各个地区的10个需求点配送茶叶,其分别为需求点1、需求点2……需求点n。每个客户以经纬度坐标的形式体现,这样在程序中可以直观地得到两两需求点之间的距离,以及各个需求点到物流中心的距离,同时提供了不同需求点的需求量。为了研究方便,本文直接以地图上的最短直线距离作为配送距离,并未考虑实际交通路况等因素。需求点的实际坐标及需求量详见表1,配送中心与各需求点之间的距离详见表2。
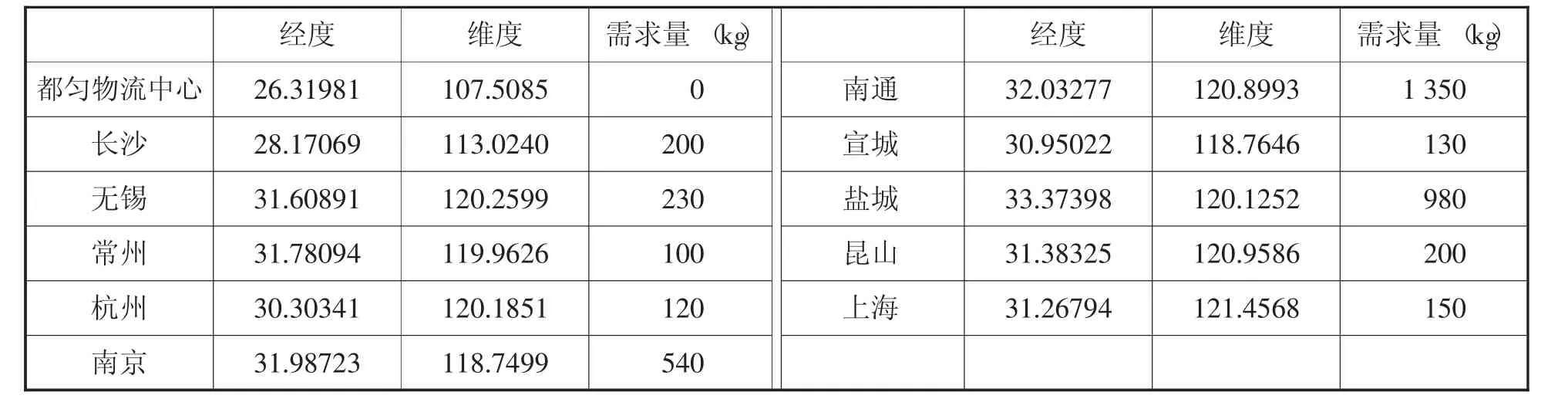
表1 需求点的实际坐标及需求量表
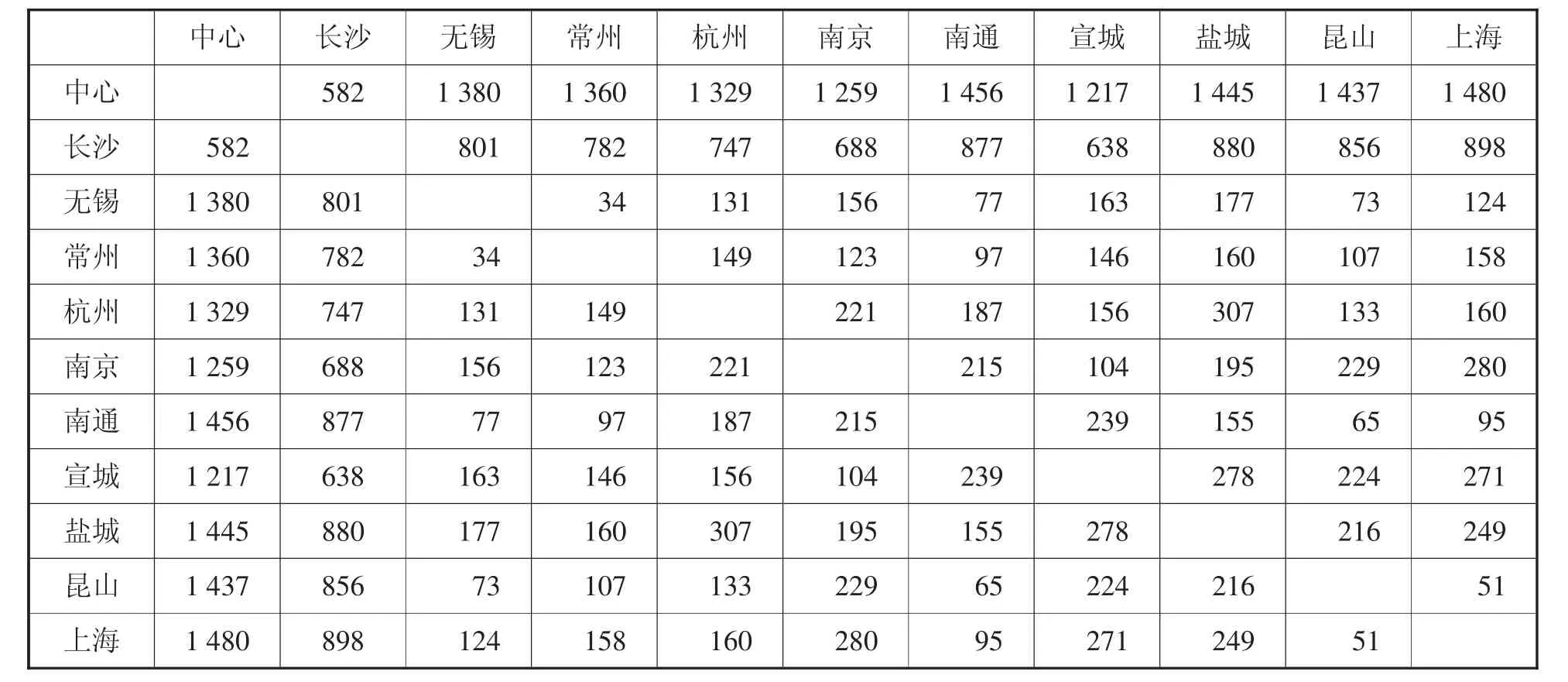
表2 配送中心与各需求点的距离 单位:km
车辆的单位运输成本h0=18元/km;车辆的固定成本O0=300元;CO2的排放系数e0=2.61L/kg,单位二氧化碳的排放成本C0=1元/kg,单位距离车辆化石燃料的消耗量p(q),在线性函数中,a=0.00347代表单位距离内车辆每增减1kg货物需要额外消耗化石燃料的系数,a=6.7498100km/L代表车辆单位距离内固定消耗的化石燃料量,单位油耗的价格k=6.74L/元。
2.2 企业不考虑碳排放的茶叶配送路径
如表3所示,在企业不考虑碳排放的情况下,2号配送路径0-2-1-3-6-4-7-5-8-9,配送里程为1 673.60km,其运输成本为30 124.79元,油耗成本为1 574.74元,固定成本为300元,总成本为31 999.54元,相较于其他配送路径,总成本最低为最优的选择[4]。

表3 企业不考虑碳排放的总成本
2.3 企业考虑碳排放的茶叶配送路径

表4 企业考虑碳排放后的总成本(二氧化碳成本1元/kg)
如表4所示,在考虑了碳排放后,3号配送路径0-2-1-8-5-7-4-6-3-9,配送里程为1 687.16km,其运输成本为30 368.83元,油耗成本为1 371.56元,固定成本为300元,碳排放成本为334.56元,总成本为32 374.94元,相较于其他配送路径,总成本最低为最优的选择。
2.4 求解结果比较
由表3和表4可知,不考虑碳排放成本不等于没有碳排放,碳排放依然客观存在着,继而比较配送路径2(0-2-1-3-6-4-7-5-8-9)和配送路径3(0-2-1-8-5-7-4-6-3-9),在考虑碳排放后,总成本下降了8.72元。这是因为考虑碳排放之后,碳排放成本对整个总成本产生了影响,最终导致配送路径方案的改变。由于碳排放的价格0.5kg/元,价格仍然处于较低的位置,在成本中所占比重较小,因而无法从经济的角度法直观地了解碳排放的影响作用。配送路径3(0-2-1-8-5-7-4-6-3-9)的配送距离为1 687.16km,相比配送路径2(0-2-1-3-6-4-7-5-8-9) 1 673.60km,增加了0.81%,而碳排放量减少了12.9%,降低了10%以上的碳排放量。那么,将二氧化碳排放成本提高至C0=20元/kg。

表5 企业考虑碳排放后的总成本(二氧化碳成本20元/kg)
如表5所示,在二氧化碳成本20元/kg的情况下以上四种配送路径情况的总成本依次为2>1>4>3,而在不考虑碳排放时的总成本依次为2<3<4<1。在未来环境保护及节约能源的大环境下,碳排放的比重将会越来越大,而考虑碳排放之后的路径将比不考虑碳排放的结果更为优化。
由上分析可知,二氧化碳排放对成本影响很大,二氧化碳成本排放最低的3号路径和排放最高的2号路径相差了991.26元,而在二氧化碳排放成本1元/kg时差距则只有49.56元。重视二氧化碳排放继而减轻二氧化碳排放是路径规划中需要重视和考虑的问题,这在很大程度上能实现降低成本的同时为低碳经济添砖加瓦。
3 结论与展望
本文在约束条件下应用蚁群算法,用其来解决本文为考虑碳排放因子所构建的物流配送路径优化模型。使用了Matlab软件对算法进行了求解并独立运行此算法程序,以此得到算法的最优配送路径方案,并且比较和分析考虑碳排放和不考虑碳排放的两条不同路径。考虑到本文建立的碳排放量的约束条件,运用蚂蚁算法对于求解茶叶物流配送路径优化模型有很大帮助。
