基于限制博弈的具有容量限制的易腐品联合运输费用分摊问题
2018-10-16单而芳梁莉敏
单而芳, 梁莉敏, 张 广
(上海大学管理学院, 上海 200444)
1 引言
易腐品,尤其是生鲜农产品的新鲜度对其销售价格有极大的影响。因此,保证易腐品的新鲜度对保证零售商的利润具有重要的意义。易腐品的新鲜度通常会随着时间的流逝而下降,在其整个生命周期中, 效用呈现递减趋势[1]。张琳和庞燕[2]指出,我国蔬果在运输过程中的损失率高达30%~40%。
目前易腐品运输问题的研究主要有两个方面。第一方面是主要研究在新鲜度或易腐品最终质量与运输过程中各种影响因素(运输设施、运输时间、保鲜技术等)之间的关系。van Arsdel和Guadagni[3]研究了冷冻食品的最终质量与流通阶段的温度、流通时间等的关系,并得到“温度越低(一定限度内),冷冻食品的质量下降越慢,保质期也相应延长”的基本结论。因此在易腐品存储与运输过程中,冷藏或冷冻技术的使用在为易腐品提供安全保障的同时, 也可以有效地延缓易腐品新鲜度降低的速度,进而保证了易腐品零售商的销售利润。Sider[4]指出在竞争性市场环境下,易腐品的零售商可能会以较高的运输成本来减少运输时间,从而通过保持易腐品的新鲜度来获得较高的市场价格,进而得到更高的销售利润。张玉洁[5]研究易腐品分类以及特点,并指出易腐品运输组织应注意的问题、原则、鲜活货物运输的特点及组织方法。
第二方面主要研究易腐性产品的运输协调问题。Hsu等[6]研究了易腐性产品的运输路径选择问题,旨在运输过程中,通过协调行驶时间和温度,进而保证易腐品的新鲜度。朱丽君[7]综合考虑了在供应商管理库存的模式下,供应商向需求商配送两种可以相互替代产品,同时考虑需求商的时间窗要求,以运输成本和货损成本最小为目标函数,建立易腐农产品调度问题模型,利用粒子群算法求解,仿真结果验证了模型和算法的有效性。张奕和傅少川[8]研究了一个易腐品供应商使用多个运输设施进行配送的库存路径问题,通过建立随机需求的多周期易腐品库存路径问题模型,将库存控制和路径选择整合优化。林峰、贾涛和李然[9]同样研究了一个易腐品供应商给多个客户进行配送的库存路径问题,创新性的考虑了在运输过程和销售过程中产品具有不同的腐败速率,以包括生产、配送、腐败、库存成本在内的供应链总成本为目标函数,建立了总成本最小化的模型。从文献综述看来,易腐性产品库存路径问题是研究的热点,但鲜有论文研究运输设施选择问题,且大部分为定性分析,缺乏定量分析。李军和蔡小强[10-11]讨论了易腐品的运输设施选择问题,并通过构建线性价值和负指数价值损失函数来衡量因易腐品新鲜度下降而造成的损失,他们没有考虑运输设施所采用的冷藏或冷冻技术有减缓易腐品新鲜度下降速度的作用。
在零售商需求量不大的情况下不同的零售商通常会考虑联合运输,即选用同一个运输设施来满足他们的需求,最后再共同承担运输的各项费用。此类问题通常称作易腐品联合运的费用分摊问题。该问题的关键在于费用分摊方案的设计。若费用分摊方式不合理,就会导致某些参与联合运输的零售商因负担了相对较多的费用而拒绝合作,最终导致联合运输联盟的破裂。因此, 制定一个公平合理的成本分摊规则是合作能够持续进行、提高运输效率的关键。
许多学者从不同的角度研究了收益及费用的分配方法。Yong[12]研究了成本分摊问题的基本方法、原则及相关应用。在各类政治、经济和社会活动中,合作共赢是人们关注的焦点问题, 由于合作博弈能够给出公平合理的利润分配方案或成本分摊规则,因此它被广泛应用到各个领域。Drechsel[13]研究了物流运输中的利润分配和成本分摊问题。对河流沿线城市水资源分配问题,Ambec和Sprumont[14]进行了深入研究。 Gilles[15]对具有等级划分的组织的利润分配问题进行了讨论,而Guan Xin等[16]则利用合作博弈解决通讯网络搭建及选址问题。关于运输费用分摊问题,曾银莲等[17]和曾银莲[18]研究了两种合并运输策略下的成本分摊博弈模型,并设计了具有稳定性的分配方案,即支付向量是核中的元素。Su Luan和Hu Dawei[19]利用合作博弈为旅游景点的公共运营车辆与私人营运车辆的合作提供合理的利润分配方案,使公共运营车辆与私人营运车辆的合作联盟更稳定,从而增加旅游景点的整体社会效益。冯海荣、李军和曾银莲[20]研究了在各零售商独立采购时基于两级信用支付的库存模型。并应用合作博弈理论,将联合采购下的费用分配问题构造成基于两级信用支付的易腐品联合采购博弈。研究表明,与各零售商独立采购相比,联合采购降低了各零售商的总费用,提高了产品的补货频率,减少了由产品变质带来的损失。
核心是合作博弈中重要的解概念,作为合作博弈的一个稳定解,核对应的分配方案是一个公平的分配方案。不过,对于许多合作博弈,确定其核分配是NP-难问题。人们在研究运输博弈时[21],考虑到运输博弈属于线性规划博弈,因此常把研究的关注点放在核非空与线性规划松弛的对偶最优解之间的关系上。Goemans和Skutella[22]证明了无约束运输设施选址问题其核非空当且仅当其线性规划松弛无整数间隙(Integrality gap)。但同时也证明了判定线性规划松弛是否无整数间隙是NP-完全问题。人们注意到凹博弈的核一定非空,因此具有凹性的博弈模型被广泛研究。李军和蔡小强[10-11]建立了具有固定运输费用的易腐性产品联合运输的费用分摊博弈模型,证明该博弈为凹博弈,并得到在易腐品线性价值以及负指数价值损失的情况下,核分配非空的结论。他们也讨论了当每个运输设施只能执行两项任务时的运输设施选择问题,并得到结论:当该问题的线性规划松弛问题无整数解时该博弈的核不存在;最后他们指出有约束的运输设施选择博弈的核有可能为空。
在经典的合作博弈中,通常假定所有的合作联盟都可以形成,并且这些联盟会影响到各参与者最终的支付[23]。然而,在现实生活中,由于受到某些因素(例如,地域、文化背景、社会地位等)的影响,并非所有的联盟都能形成。这促使了具有限制结构的合作博弈(简称为限制博弈)的产生。其中,Aumann和Dreze[24]研究了具有联盟结构的限制博弈。Myerson[25]则研究了具有图结构的限制博弈。通常,限制博弈可以被定义为一个三元组(N,c,Ω),其中N为有限的参与者集合,c为特征函数,Ω为可行联盟(即可以形成的联盟)的集合,并且φ,N∈Ω,即空集和大联盟均是可行联盟[26]。Faigle[27]研究了大联盟不是可行联盟的情况(即N∉Ω),进而定义了一个四元组(N,c,Ω,c0),其中c(N)=c0。可行联盟集Ω通常有多种表现形式,例如,Owen[28]定义的优先联盟(即在博弈开始之前参与者约定结盟并统一行动),Myerson[25]通过图结构假定只有连通的参与者才能形成联盟, 而Gilles和Owen[29]则通过准许结构假设参与者要获得其上级的同意才可以形成联盟等。此外,Bilbao[30]给出了凸几何结构的特点。
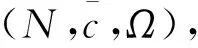
2 问题的模型描述及相关符号
我们考虑某一区域的易腐品零售商在某个时间段T需要一定量的同种易腐品,且市场上有一些具有不同运输时间、保鲜技术和运输费用的运输设施可以选择。
对于一个易腐品零售商来说,在选择运输设施时,他需要考虑运输成本、运输时间和保鲜效果。本文将易腐品新鲜度的变化量价值化,将它看作为费用。因此零售商要承担包括运输成本和易腐品新鲜度下降带来的损失在内的总费用。在易腐品需求量不大的情况下,一些零售商可以考虑选择同一个运输设施来实现联合运输。这就是找到一个运输设施使总费用最小的设施选择问题。
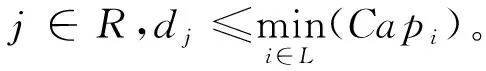
通常,用新鲜度因子来刻画易腐品的新鲜度。但在不同的情况下新鲜度因子的定义也不一样。但斌等[31]通过构建具有加速衰减特征的指数函数θt=θ0e-ηt来作为生鲜农产品新鲜度因子的表达式,并建立了考虑消费者效用与保鲜的易腐品EQO模型。李滢棠[32]认为果蔬品供应链网络中的某节点的新鲜度因子的大小取决于其上游的节点的果蔬品新鲜度因子的大小,并通过θi=f{θi-1}来表达果蔬品新鲜度的迭代关系, 并在此基础上研究了供应链协同决策的问题。
本文借鉴新鲜度因子的概念,将运输设施i对易腐品新鲜度的影响Δθi定义为:Δθi=eηti-ui。 其中η表示易腐品新鲜度随着时间衰减的速度,η>0,η越大表示易腐品新鲜度衰减速度越快,η由易腐品的种类决定。ηti-ui≤0即保鲜技术仅能起到保持易腐品新鲜度的作用,无法使易腐品新鲜度提高。本文定义易腐品新鲜度对价格的影响为:Δp=aΔθ,其中a为新鲜度对价格的影响系数,a>0,易腐品的种类不同,a值也将不同。
定义1 对于i∈L,j∈N,易腐品运输设施选择问题定义为:
(1)
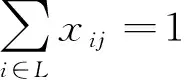
(2)
xij≤yi∀i∈L,j∈N
(3)
xij,yi=0或1
(4)
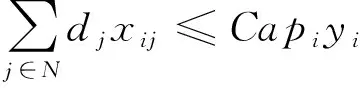
(5)
其中yi=1时,表示运输设施i开放,可以被使用,i∈L,否则yi=0。xij=1时,表示零售商j选择运输设施i,∀i∈L,j∈N;否则xij=0。
目标函数(1)表示总费用(包括固定费用, 变动成本和因新鲜度下降导致的价值损失)最小;约束(2)-(3)保证了每个零售商仅被一个开放的运输设施服务;约束(5)确保零售商的总需求不超过其所选定的运输设施的容量。
上述模型的目的是对考虑容量限制的运输设施选择问题,找一个极小化总费用的最佳方案。考虑对应于选择的运输设施,是否总费用能够被公平地、平稳地在所有零售商之间进行分摊。
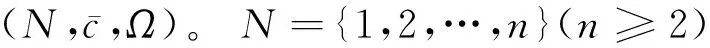
即可行联盟内所有零售商的运输需求总和不能超过所有种类的运输设施的最小容量,Ω为所有可行联盟的集合。对于所有的可行联盟T∈Ω:
对于所有S∉Ω,S可以划分成有限个可行的子联盟,且各个可行子联盟之间互不相交,那么就记这种划分的集合为P(S,Ω),则:
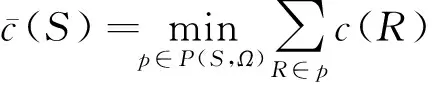
注意到当S∈Ω时,P(S,Ω)={S}。因为考虑了容量限制,所以大联盟N∉Ω,则必然存在划分p*,使大联盟的费用最小,也即:
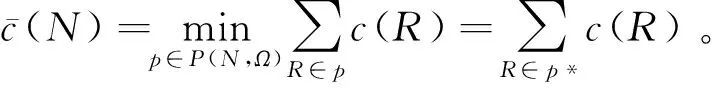
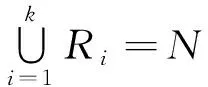
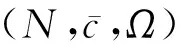
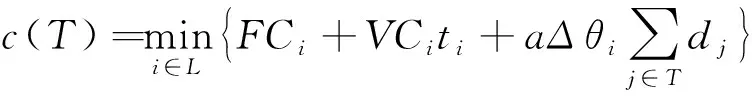

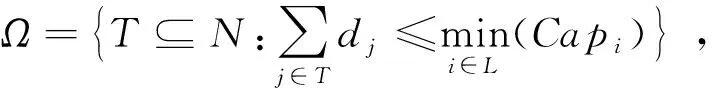
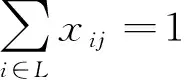
xij≤yi∀i∈L,j∈R。
xij,yi=0或1。
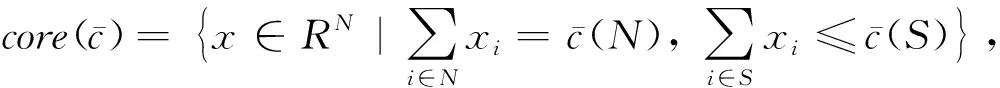
3 易腐品联合运输费用分摊博弈的特征
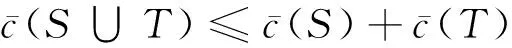
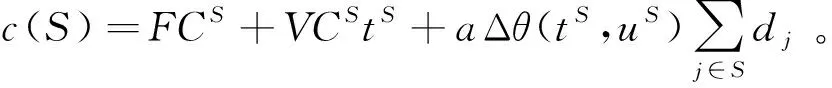
(1)对于所有S,T∈Ω,S∩T=φ且{S∪T}∈Ω,则有:
和
因为{S∪T}∈Ω,则
和
那么,我们有:
(6)
和
(7)
若FCS>FCT,则Δθ(tS,uS)<Δθ(tT,uT),所以(6)<0。也即:
(8)
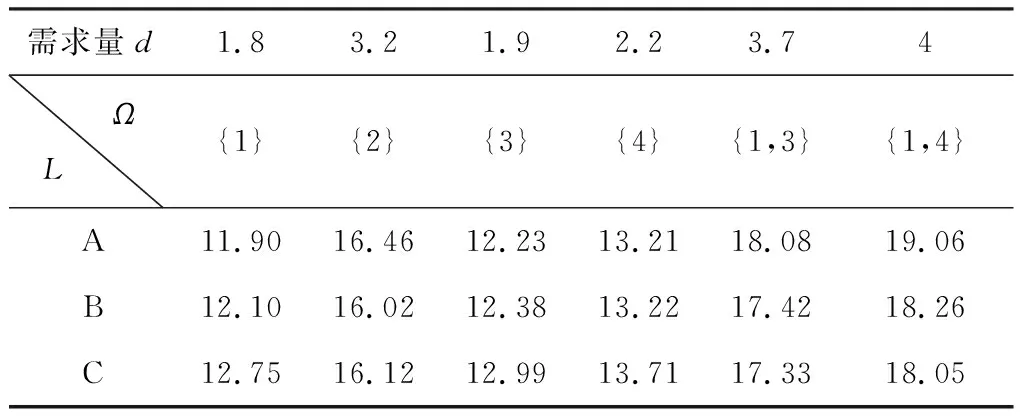
若FCS (9) (2)对于所有S,T∈Ω,S∩T=φ且{S∪T}∉Ω,则联盟S∩T可以划分为有限个可行子联盟R,且各个子联盟之间互不相交,这种划分记为P(S∪T,Ω),那么 因为{S∪T}∈P(S∪T,Ω),易得: (3)对于所有的S,T∉Ω,S∩T=φ,则有S∪T∉Ω。不可行联盟S的划分为P(S,Ω);T的划分为P(T,Ω);S∪T的划分为P(S∪T,Ω)。 因为(P(T,Ω)∪P(S,Ω))⊆P(S∪T,Ω),所以 (4)对于所有S∈Ω,T∉Ω,且满足S∩T=φ和S∪T∉Ω。则联盟S的划分为P(S,Ω),联盟S∪T的划分为P(S∪T,Ω)。 因为对于所有的p(S,Ω)∈P(S,Ω),都满足(p(S,Ω)∪T)∈P(S∪T,Ω)。易得: 命题1说明不同的零售商之间合作选择同一运输设施来运输他们需要的易腐品会更节省成本,进而说明易腐品零售商之间的合作是有意义的。 命题2 若S⊆T∈Ω, 则对应于c(S)和c(T)的新鲜度衰减程度Δθ(tS,uS)和Δθ(tT,uT),有Δθ(tS,uS)≥Δθ(tT,uT)。 证明:因为 (10) (11) (12) (13) 从而可得: 其中,不等式的左侧由式(12)减去式(11)得到,而右侧由式(13)减去式(10)得到。整理后可得Δθ(tS,uS)≥Δθ(tT,uT)。命题2得证。 命题2说明运输量越大的联盟更愿意选择固定成本(FC)等大,但运输时间更短,保鲜技术更好的运输设施来减少易腐品运输过程中因易腐品新鲜度下降造成的损耗。 证明:令 而 由于 所以 又由于 所以 综上可得: aΔθ(tT∪{i},uT∪{i})d{i}≤h(T,{i})≤aΔθ(tT,uT)d{i} 同理,我们有 aΔθ(tS∪{i},uS∪{i})d{i}≤h(S,{i})≤aΔθ(tS,uS)d{i} 容易得到 h(S,{i})-h(T,{i})≥ad{i}[Δθ(tS∪{i},uS∪{i})-Δθ(tT,uT)] (14) 又因为 因此可得: (15) 当Δθ(tT,uT)≤Δθ(tS∪{i},uS∪{i}),由式(14)得h(S,{i})-h(T,{i})≥0;否则,由式(15)得h(S,{i})-h(T,{i})≥0。即: 恒成立。命题3得证。 命题3说明一个易腐品零售商或可行联盟更愿意加入规模更大的可行联盟。下面的命题给出了限制核非空的充分条件。 Rl(T∪{i})=Rl(T)或Rl(T)⊂Rl(T∪{i})。 因为Rl(T),Rl(S),Rl(T∪{i}),Rl(S∪{i})∈Ω,l=(1,2,…,k),因此由命题3易得下面的式子成立:对每个l=1,2,…,k, c(Rl(T)∪{i})-c(Rl(T))≤c(Rl(S)∪{i})-c(Rl(S)) (16) 易腐品零售商N={1,2,3,4},4个零售商各自的需求d={1.8,3.2,1.9,2.2}。 运输设施集L={A,B,C},有固定成本FC={FCA,FCB,FCC}={0.8,3.7,6.2},单位时间的变动成本VC={VCA,VCB,VCC}={1.5,1.4,1.3},运输时间t={tA,tB,tC}={3.5,2.4,1.7},保险技术因子u={uA,uB,uC}={1.25,1.29,1.37},载荷量Q={QA,QB,QC}={4,5,4}。 假定所有的易腐品零售商运输同一种易腐品,则新鲜度对价格的影响系数a和易腐品新鲜度随着时间衰减速度η是统一的,a=8,η=0.1。此时,容易得到可行联盟集为: Ω={{1},{2},{3},{4},{1,3},{1,4}}。 所有可行联盟选择各个运输设施所产生的总成本计算如表1。 表1 可行联盟选择各个运输设施所产生的总成本 x1+x2+x3+x4=46.30 其中x(S)=∑i∈Sxi。该限制核非空,x1={5.0582,16.02,12.23,12.9918}位于限制核里。 我们分别计算Shapley值φ(S),τ-值和核仁η(S)(见表3)。 表2 限制博弈的特征函数值 表3 限制博弈的一些解 由表3可以知道:τ-值τ(S)和核仁η(S)和Shapley值φ(S)都不在和核心中。 随着社会经济的发展,人们对易腐品的需求越来越大,而质量要求也越来越高。因为易腐品的运输呈运量小批量化的特点,所以易腐品零售商采用联合运输,共同选择性能好的运输设施。 本文考虑了运输设施的保鲜技术对易腐品新鲜度的影响,建立考虑容量限制的易腐品运输设施选择问题模型,并借鉴限制博弈的可行联盟的思想将该模型的费用分摊问题转化为限制博弈模型,最后通过证明该限制博弈的凹性,得到了该限制核非空的充分条件。研究结果表明,在多个零售商合作选择运输设施来运输生鲜农产品时, 则倾向于选择一个租金较昂贵的运输设施,此时来获得更短的运输时间和更好的保鲜技术来降低总成本。本文研究的易腐品运输设施选择问题只是一类情形。事实上,有时产品质量等因素也有限制要求,此类约束的运输设施选择博弈还待进一步研究。 致谢: 感谢评审专家的仔细阅读和有价值的建议。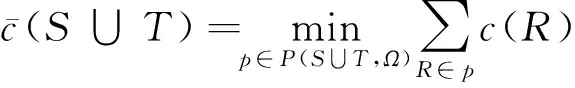
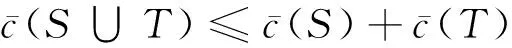
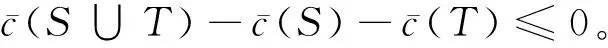
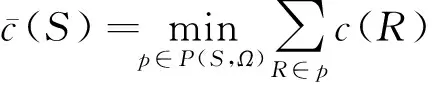

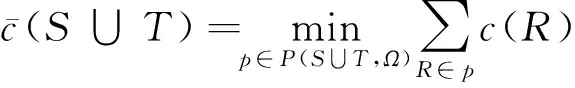
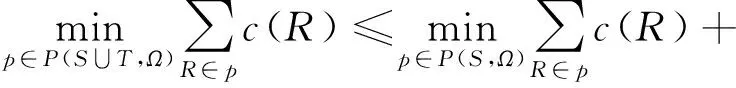
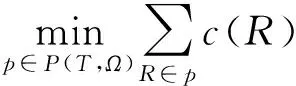
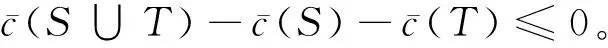
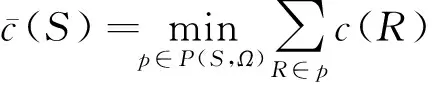
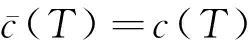
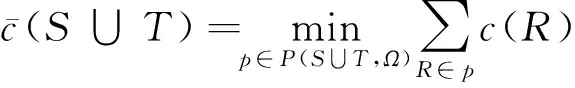
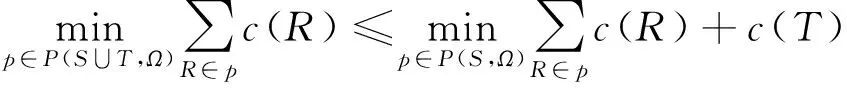
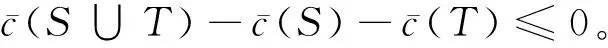
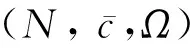
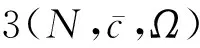
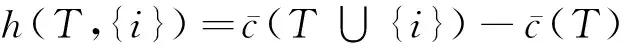
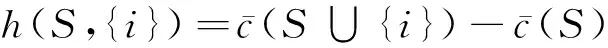



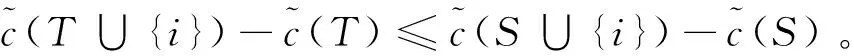
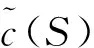
4 实例分析
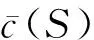

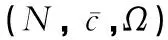
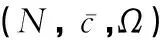
5 结语
