考虑决策者损失规避的异质信息多属性变权决策方法

余高锋, 李登峰,吴 坚,叶银芳

(1.福州大学经济与管理学院，福建 福州 350108；2.三明学院信息工程学院，福建 三明 365004；3.上海海事大学经济与管理学院，上海 201306)

1 引言

多属性决策是现代决策理论的重要组成部分，在经济、社会、科技、文化以及企业的生产运营管理和人们的日常等方面都具广泛应用。在现实决策问题中，模糊集[1]能够较为客观反映现实问题的模糊性，但模糊集只能描述隶属度的信息，由于现实决策问题复杂性，决策者往往会表现一定犹豫，即直觉模糊集[2]同时考虑隶属度、非隶属度和犹豫度三方面的信息，在模糊集的基础推 广和发展，能够较好的刻画决策者对现实问题表现的犹豫性和不确定性。基于不确定信息的多属性决策方法与应用得到广泛深入的研究[4-10]，例如直觉模糊多属性决策[3]、混合型随机多属性决策方法[4]、犹豫模糊随机多属性决策方法[5]、多属性相对变权决策方法[6]、区间直觉模糊决策方法[7-8]、三角模糊直觉决策方法[9]和行为多属性决策方法[10]等。

在研究多类评价信息方面，李登峰等提出方案偏好具有不确定性的异质信息模糊多目标决策方法[11-13]、方案偏好具有不确定性的异质信息模糊多目标多人决策方法[14-16]、不完全信息多类型属性值的异质信息模糊多目标决策方法[17]等。另一方面，梁昌勇等[18]建立将多类评价信息统一转化为区间直觉模糊数的混合型多属性决策方法. 樊治平等[19-20]建立一种基于累积前景理论的混合型多属性决策和风险型混合多属性决策方法. 万树平等[21-22]将多类型评价信息转化为直觉模糊和区间直觉模糊进行多属性群体决策，余高锋[23]等建立基于变权分析方法的异质信息多属性决策方法，余高锋等[24-25]建立基于行为激励型变权决策方法和局部变权决策方法的企业质量信用评价模型。

上述提及的研究成果为解决模糊多属性决策问题提供较好的思路，但是由于决策问题的复杂性和不确定性以及人类思维的模糊性，决策者很难对方案给出精确的评价，会遇到属性权重与属性值的具体状态和决策者心理行为有关，以及同时涉及定性定量信息等决策问题，即考虑决策者损失规避和异质信息变权决策方法。因此，基于变权分析的有限理性异质信息多属性决策问题是值得研究的。为此，本文提出一种同时考虑异质信息、决策者的有限理性和属性权重随属性值变化的决策方法，为解决具有异质信息的实际管理决策问题提供新思路和新方法。

2 问题描述

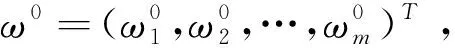
设决策者对指标ci的评价值为:

(1)

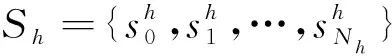
3 决策方法

3.1 异质信息规范化

为了消除物理量纲的影响， 需要进行无量纲处理，结合Wang Shuping和Li Dengfeng[11]， 具体如下:

(2)

和

(3)

3.1 异质信息相对贴近度

(4)

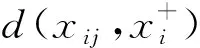
和

3.2 属性权重的益损值

设zj=(z1j,z2j,…,zmj)为方案aj与异质信息正理想解的相对贴近度、S(zj)=(S1(zj),S2(zj),…,Sm(zj))T为状态变权向量，其中S(zj)是某个实值函数B(zj)的梯度向量，即由下面分向量组成：

称B(zj)为均衡函数。

(5)

其中符号“⊗”表示2个向量的Hardarmard乘法。

依据余高锋等[26]可知，若B(zj)为保守型效用函数，w(zj)为惩罚型变权向量；若B(zj)为风险型效用函数，w(zj)为激励型变权向量；若B(zj)为S型效用函数，w(zj)为折衷型变权向量；若B(zj)为中间型效用函数，即w(zj)=ω0，常权可看作为变权的特殊情况。

把式(5)记做w(z)=(wi(zj))m×n，选初始权重为参考点，可建立变权向量相对初始权重的权重益损矩阵F=[F(wi(zj))]m×n，其计算公式如下：

F(wi(zj))

(6)

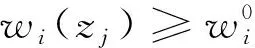
依据权重的益损矩阵F=[F(wi(zj))]m×n，考虑决策者对待权重的收益和损失的不同风险态度，可建立前景理论矩阵V=[v(wi(zj))]m×n，其中

V(wi(zj))

(7)

其中参数α和β表示函数V(wi(zj))的凹凸程度，0≤α≤1，0≤β≤1；参数θ表示决策者的风险规避程度。曾建敏[27]则认为在中国国情下，风险偏好系数是敏感性增强的，θ=2.25，而α=1.21，β=1.02。本文系数采用中国国情下的系数即：α=1.21、β=1.02。

因此计算每个方案的综合前景值U(aj)如下：

(8)

根据上面的讨论，提出基于有限理性的异质信息多属性变权决策方法的具体步骤如下：

步骤1: 识别、确定待评价的所有方案A={a1,a2,…,an}和属性C={c1,c2,t…,cm}。

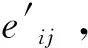
步骤3：根据式 (4) 计算各个方案与异质信息正理想解的相对贴进度，其中利用式 (2) 和 (3)将异质信息去量纲。

步骤4：根据决策者的心理行为特征和各个方案的相对贴近度，利用选取风险型效用函数、保守型效用函数和中间效用函数等，结合式 (5)， 构造不同类型变权向量，计算属性的变权权重。

步骤5：利用式 (6) 和 (7) 分别计算属性权重的益损矩阵和前景矩阵。

步骤6: 依据式 (8)，计算每个方案的综合前景值，并根据综合前景值的大小对所有方案进行排序。

4 实例计算与分析

4.1 实例计算

精准扶贫成效第三方评估指标体系可以定义为一系列相互联系的能敏感地反映精准扶贫成效状态及存在问题的指标的有机构成整体，为了准确地测量精准扶贫成效水平，从精准扶贫业务流程的关键环节中筛选反映精准扶贫成效水平的评价指标时必须遵循的敏感性、内容的代表性、范围的全面性、指标的可测量性、数据的效用性和体系的稳定性等原则，构建了一套相对比较完整的优选指标体系。该指标体系主要从贫困对待评价的精准扶贫成效第三方进行考量。构建的具体指标有对帮扶方式满意度、贫困户识别准确率、驻村干部工作满意率帮扶成效帮扶责任人到贫困户家中未到次数等。

精准扶贫成效第三方评估指标体系涉及到的指标值类型主要有：实数、区间数、三角模糊数、语言变量和直觉模糊数等。其中，关于帮扶责任人到贫困户家中未到次数指标，以实数形式表示。对衡量驻村干部工作满意率因受多种不确定因素的影响，在不同的时间段会表现出一定的波动性，因此采用区间数的形式表示，类似地，贫困户识别准确率利用三角模糊数表示；针对定性指标，比如：帮扶成效无法用具体数值衡量的指标，对其衡量是通过相关专家的语言描述，以语言变量的形式衡量；对帮扶方式满意度进行评价时可能会分别给出满意、不满意、犹豫，即采用直觉模糊数表示。

根据《XX市2016年扶贫开发工作成效第三方评估实施方案》，XX市应对全市十二个县市区进行扶贫实施效果的评估，特委托第三方开展此次工作。2016年扶贫工作成效第三方评估的对象为XX市2016年及以前建档立卡识别的贫困户和脱贫户。设指标属性权重为

本次第三方评估在XX市扶贫办提供的2016年贫困户信息系统基础上，选择了5个乡镇对精准扶贫成效第三方评估，具体评价信息如下：

(1) 根据式 (2)～(3)，对决策矩阵进行规范化，结果如下：

(2)决策者对方案aj与异质信息正理想解的相对贴近度为：

其中异质信息正理想解x+和负理想解x-分别为：

x+=(<0.7,0.1>,(0.90,0.96,1),[0.7,1],(s5,0),0.1667)

x-=(<0.3,0.6>,(0.32,0.80,0.90),[0.2,0.8],(s1,0),0)。

(3)结合决策者的偏好，以p参考点， 构造S型效用函数如下：

(9)

若p=0.5时，有：

即

其中i=1,2,…,5;j=1,2,…,5。经计算，得到各个方案属性的变权权重矩阵如下：

根据式(6)， 计算变权向量相对于参考点(初始权重)的收益和损失，并建立相对参考点的益损决策矩阵：

F=

(4)依据式 (7)，计算各个属性权重的前景值，即前景矩阵如下：

V=

其中α=β=0.88和θ=2.25。依据式(8) ，计算各个方案的综合前景值为：

U(a1)=0.0015,U(a2)=-0.003,U(a3)=-0.0208,U(a4)=0.0009，U(a5)=-0.0154。

因此， 5个乡镇的精准扶贫成效水平如下:

a1≻a4≻a2≻a5≻a3。

4.2 灵敏度分析

为了说明参考点对决策结果的影响， 改变参考点的取值，重复步骤 (3) 和 (4), 所得结果如下表2所示。

由表2可知，保守型效用函数诱导的是惩罚型变权向量，而变权向量相对初始权重，大部分都是损失，即综合评价值大部分都小于零；风险型效用函数诱导的是激励型变权向量，而变权向量相对初始权重，都是收益，即其综合评价值大于零。S型效用函数诱导的是折衷型变权向量，而变权向量相对初始权重，有损失，也有收益，即其综合评价值有大于零，也有小于零。另外，不同参考点的评价结果的排序不同，特别地保守型效用函数、风险型激励函数和S型效用函数的最优方案都不同，特别地不同参考点的S型效用函数的最优方案相同，但是各方案排序不同。因此，本文方法充分体现过程的柔性和决策者的有限理性。

表2 不同参考点的评价结果

4.3 与已知方法对比分析

文献[18]仅考虑多类定性评价信息， 将多类评价信息统一转化为区间直觉模糊数，另外文献[21，22]也把异质信息统一转化为直觉模糊数和区间直觉模糊数等，而本文同时涉及定性定量评价信息，利用相对贴进度进行处理，有效避免信息丢失和扭曲。

本文提出基于变权向量相对于初始权重的权重益损决策方法， 然而樊治平等[19]和李鹏等[20]通过计算属性值相对参考点的综合前景值进行方案排序，前后两者的研究方法研究视角截然不同，为解决行为决策提出一种新的方法。

5 结语

本文研究了一种基于前景理论和变权分析方法的异质多属性决策的求解方法。该方法决策者选择保守型效用函数、风险型效用函数和S型效用函数等构造变权向量，计算变权向量相对初始权重损失和收益具有不同风险态度等前景综合值，依此给出方案的排序结果，为解决具有多种类型信息的实际管理决策问题提供新思路、新方法和技术支持。另外，本文方法在流域生态安全评估、河流健康发展评估、旅游安全风险预警和跨境电子商务供应链风险预警等实际问题也有广泛应用。