圆柱形钨破片撞击铝靶时的跳飞临界角*

2018-10-16蓝肖颖李向东周兰伟宫小泽姚志军

爆炸与冲击 2018年6期

蓝肖颖，李向东，周兰伟，宫小泽，姚志军

(1.南京理工大学机械工程学院,江苏南京 210094；2.中国白城兵器试验中心,吉林白城 137001)

破片是很多战斗部杀伤目标的毁伤元素，是用于穿透部件结构、杀伤有生力量、毁坏战场目标的功能部件。当破片以大着角撞击目标或部件蒙皮时，靶板的反作用力使破片运动方向发生偏转，破片会在翻转力矩作用下发生跳飞，无法持续侵入靶板。破片跳飞影响其后续侵彻能力，达不到预定的毁伤效果，因此研究破片跳飞的条件及影响因素对战斗部设计和毁伤效能评估等都具有非常重要的意义。

相关的研究主要针对长径比较大的弹丸(如穿甲弹、榴弹等)。赵国志[1]建立了长杆弹斜侵彻有限厚钢板的简化模型，得出了长杆弹发生跳飞的条件。吴荣波等[2]对弹丸以不同入射角侵彻半无限厚靶板进行了数值模拟，得出入射角不大于75°不能发生跳飞的结论。董玉财等[3]研究了钨合金长杆体侵彻薄装甲钢靶板上的跳飞特性，得出随着靶板厚度的增加，着角因素对跳飞的影响呈强化趋势，而靶板厚度因素呈逐渐弱化趋势的结论。米双山等[4]利用数值模拟方法研究了球形破片侵彻不同厚度靶板的过程，得出了破片穿透靶板和跳飞的临界值。Tate[5]、Rosenberg等[6]、Segletes[7]分别建立了关于长杆弹的不同跳飞模型，但模型均未考虑到靶板厚度对跳飞角的影响[5-7]。Zook等[8]利用X光摄影实验的方法对钢球冲击铝板的现象进行了研究，实验得到破片斜侵彻过程中速度衰减规律与靶板厚度、入射角度的关系。

本文中主要研究圆柱形破片(3.13 g)以800～1 200 m/s的速度撞击有限厚铝板时的跳飞临界角，并分析靶板的厚度、入射速度对跳飞临界角的影响。

1 破片跳飞临界角计算模型

1.1 破片斜侵彻过程受力分析

当破片以较大的入射角撞击靶板时，在靶板抗力的作用下，破片的运动方向发生改变，出现跳飞。过程如图1所示。

破片撞击侵入靶板的各个状态如图2所示，图2(a)表示破片刚接触靶板，图2(b)表示破片在靶板中运动至靶板底面的过程，图2(c)表示破片开始穿出靶板一定距离。为了便于分析破片的受力及跳飞条件，假设破片撞击侵入靶板过程中不变形。破片受力情况如图2(b)所示，侵彻阻力F1、F2等于靶板强度极限乘以破片和靶板的接触面积[9]，即：

F1=σtS1

(1)

F2=σtS2

(2)

式中:σt为靶板材料强度极限；S1、S2分别为破片前端和侧面与靶板的接触面积，即分别为图2(b)中AB段所对应的面积和BC段所对应的面积。接触面积的计算分两种情况，即破片未穿出靶板和破片部分穿出靶板：

(3)

(4)

式中:r为破片半径,H为破片的高度,h为靶板厚度,l为撞击过程中破片在靶板内的运动距离,α为速度方向与靶板法线方向的夹角,L为破片未穿出靶板前侵入靶板的距离,d为破片前端穿出靶板的距离。其中l、A、A1、d、L的表达式分别为:

(5)

(6)

(7)

(8)

(9)

1.2 破片的运动及跳飞条件

作用在破片质心的力矩Mc使破片在侵彻过程中发生偏转，使速度方向与靶板法线方向的夹角α在侵彻过程中发生变化。α与破片角速度ω的关系为：

(10)

式中：α0为破片撞靶时速度方向与靶板法线的夹角(入射角)。

破片偏转的角速度与角加速度的关系为：

(11)

式中：Jc为破片绕质心转动惯量。

作用在破片质心的力矩Mc与破片受到的侵彻阻力F1、F2有关，所受的阻力矩M1、M2分别为：

(12)

(13)

由式(12)～(13)，可求出作用在破片质心的力矩：Mc=M1+M2。结合式(10)～(11)可求出任意时刻的α角。

在力F1和F2的作用下，破片速度减小，如图2所示，取向下为正，若出现跳弹现象，破片剩余速度在y轴的分量必会反向，即沿着y轴的速度分量小于0时跳飞。综合以上式子可得：

(14)

由式(14)可求得v，当vy=vcosα<0 时，破片跳飞，由此可求得破片跳飞临界角αcr。

1.3 破片跳飞临界角计算

根据上述模型，计算了圆柱形破片以800～1 200 m/s的速度撞击2～10 mm厚的2A12 T4铝板时的破片跳飞临界角。其中，破片材料为钨，密度为18.3 g/cm3，直径5.7 mm，高度6.7 mm，质量3.13 g。靶板密度为2.8 g/cm3，强度极限420 MPa。计算结果如表1所示。

表1 计算得到的破片侵彻靶板跳飞临界角Table 1 Calculated results of critical ricochets of penetrators impacting targets

2 跳飞过程及临界角的数值模拟

在800～1 200 m/s的速度范围内，对圆柱形钨破片侵彻铝板的跳飞过程进行了数值模拟，计算破片撞击不同厚度(2～10 mm)铝板的跳飞临界角，本节以4 mm靶板为例分析跳飞的过程。

2.1 模拟计算模型

采用LS-DYNA有限元软件计算圆柱形破片斜侵彻2A12 T4铝合金靶板的过程。破片和靶板单元类型均选择SOLID164，网格单元采用八节点六面体。对破片直接作用的靶板区域加密，加密部分单元尺寸为1 mm，其余部分网格划分相对稀疏。破片与靶板的接触方式为ERODING_SURFACE_TO_SURFACE，破片和靶板均采用Johnson-Cook材料模型和Grüneisen状态方程。对靶板侧面施加全自由度约束和非反射边界约束。采用侵蚀算法，并与失效准则连用，当单元的有效塑性应变达到失效应变或者单元压力达到最小压力时，则单元失效，计算中失效的单元将被删除[10]。

Johnson-Cook模型的应力应变关系为：

(15)

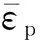
εf=[D1+D2exp(D3σ*)](1+D4lnε*)(1+D5T*)

(16)

计算时采用Grüneisen状态方程，对可压缩材料，压力的表达式为：

(17)

式中：S1、S2、S3是us-up曲线斜率的系数；c为体积声速；γ0是Grüneisen常数；μ=ρ/ρ0-1 ，ρ是当前密度，ρ0是初始密度；a是γ0的一阶体积修正。

具体的材料参数如表2所示。表中，ρ、E、μ分别为材料的密度、杨氏模量、泊松比；A为与材料屈服极限相关的常数；B、C、n为与材料的应变硬化及应变率相关的系数；m为温度系数。

表2 Johnson-Cook材料参数Table 2 Johnson-Cook material parameters

2.2 数值模拟结果及分析

在数值模拟过程中，通过每次改变1°入射角来计算破片撞击靶板时的跳飞临界角。图3～4所示为破片以1 000 m/s着速撞击4 mm厚靶板时数值模拟的过程。如图3所示，入射角为77°时，破片先开坑，然后随着侵彻的进行沿着靶板表面向前运动，继续侵彻靶板，最终穿透4 mm板。由于77°时破片没有发生跳飞，因此将入射角增大到78°重复上述计算。如图4所示，在84 μs时破片翻转跳飞。

破片的速度及姿态说明破片在侵彻过程中发生了跳飞。图5为破片分别以77°、78°入射角、1 000 m/s的速度撞击4 mm厚靶板时，破片速度沿靶板法线方向的分量随时间的变化曲线。由图5可知，入射角为77°时，破片速度分量方向并没有改变；78°时，破片速度分量方向改变，发生跳飞。结合图3～4的模拟结果可知，当破片沿着靶板法线方向的速度分量方向改变时，发生跳飞现象。如图6所示，破片开始侵彻靶板时，受到靶板的阻力，破片与靶板的夹角逐渐增大，若破片跳飞，角度会继续增大。

取跳飞和不跳飞情况入射角的平均值作为跳飞临界角，因此，以1 000 m/s撞击4 mm靶板时的临界跳飞角为77.5°。重复上述过程计算得到破片以800～1 200 m/s的速度撞击2～10 mm靶板时的跳飞临界角。

图7为理论计算得到的破片跳飞临界角与破片入射速度、靶板厚度之间的关系。由图7可知，破片的跳飞临界角随着靶厚的增加而减小，随着速度的增大而增大。由图7可知，数值模拟计算结果和理论模型计算结果吻合较好。

3 破片撞击铝靶跳飞临界角实验

3.1 实验方法

为了验证上述模型的正确性，进行了破片以不同速度撞击不同厚度靶板的实验。实验装置如图8所示，由弹道枪、破片测速系统(测速靶和测试仪组成)、靶板、高速录像机等组成，具体的实验场地布置如图9所示。通过弹道枪控制并获取破片的撞靶速度；破片测速系统测试破片撞靶时的速度；高速录像记录撞靶过程，并判断破片是否跳飞。

实验时靶板厚度选用2、4 mm两种，控制破片以800～1 100 m/s的速度撞击铝靶板。通过调整靶板的放置倾角控制破片撞靶时的入射角。若破片没有跳飞，则增大入射角度重复实验；若破片跳飞，则减小入射角度。当不跳飞的最大入射角和跳飞的最小入射角之差小于3°时，取两角度的平均值作为破片的跳飞临界角。如图10所示为高速摄影记录的破片斜撞击4 mm厚靶板过程。当撞击角度为75°、速度为1 060 m/s时，破片穿透了靶板；增大角度至77.5°，速度为1 053 m/s时，破片撞板之后发生跳飞。

3.2 实验结果及分析

参考理论及数值模拟结果，使破片以800～1 200 m/s的速度分别以80～85°的入射角撞击2 mm厚靶板，70～80°入射角撞击4 mm厚靶板，共进行了26发实验。由于实验数据较多，因此节选跳飞临界角附近的实验结果数据，如表3所示。

表4为实验得到的破片在不同速度范围内撞击不同厚度靶板时的跳飞临界角。实验得到破片撞击2 mm厚靶板的跳飞临界角为81°～81.25°，破片撞击4 mm厚靶板的跳飞临界角为72.5°～76.25°。

表3 破片撞击靶板实验结果Table 3 Experimental results of fragment impacting target

表4 破片撞击靶板跳飞临界角对比Table 4 Results of critical ricochets of fragment impacting target

4 理论、计算及实验结果的对比分析

图11(a)～(b)为破片以980 m/s的速度、82.5°的入射角撞击2 mm厚靶板的实验和数值模拟切口情况，实验靶板上的切口长59 mm、宽10 mm；模拟切口长66 mm、宽7.5 mm。图11(c)～(d)为破片以950 m/s的速度、75°的入射角撞击4 mm厚靶板的实验和模拟靶况，实验靶板上的切口长47 mm、宽8 mm；模拟切口长50 mm、宽9.5 mm。对比实验和模拟结果，破片撞击靶板后，靶板上切口形状相似，但模拟得到的切口长度比实验得到的长10%左右。这是因为模拟时，靶板单元的有效塑性应变达到失效应变时，单元将被删除[10]。

图12为破片跳飞临界角理论计算值、模拟值与实验值的对比。由图12可看出，破片以800 m/s的速度撞击4 mm板时的理论计算结果、模拟结果和实验数据的偏差最大，这可能是因为实验中存在小攻角的情况，但总体数值模拟计算和实验结果的最大偏差为1.8%、理论计算和实验结果最大偏差为3%。对比表明，理论计算结果、模拟结果和实验结果是一致的。说明所建立的理论跳飞模型及数值计算方法是正确的。