基于J-C模型的Q235钢的失效准则*

郭子涛，舒开鸥，高 斌，张 伟

(1.九江学院土木工程与城市建设学院， 江西 九江 332005；2.哈尔滨工业大学高速撞击研究中心，黑龙江 哈尔滨 150080)

金属结构因为具有强度高、可塑性好、价格低廉等优点，在军事和民用结构防护领域有着广泛的应用。金属靶受到载荷冲击、爆炸及结构碰撞等作用时将汇聚高温、高压、冲击波的传播等瞬态物理现象，同时在高温高应变率下金属靶板会产生大塑性变形、断裂破坏以至熔化和气化等相变过程。因此研究适用于描述金属材料在大应变、大应变率下及宽温度范围的力学行为失效准则，对于模拟防护结构在弹体高速撞击下的瞬态响应至关重要，对于现代防护结构的设计也有着重要意义。

材料的失效与多种因素有关并夹着复杂的物理机制，常见的有常塑性应变断裂准则、最大剪应力/主应力断裂准则、基于塑性功的C-L断裂准则以及经验型Johnson-Cook断裂准则[1]等。Y.B.Bao等[2]通过对各种形状的2024铝合金试件的材料性能实验，发现断裂应变随应力三轴度并不是单调变化，提出了一个分段函数表示的B-W断裂准则以描述断裂应变与应力三轴度的关系，陈刚等[3]在对TC4钛合金材料的破坏特性研究中也得到了类似的现象。Q235钢作为一种低碳钢材料，由于含碳适中、综合性能较好，强度、塑性和焊接等性能配合较好且价格低廉，在建筑、桥梁、船舶及结构防护领域应用广泛。对Q235钢的冲击及抗冲击性能已有一些研究，如陈小伟等[4]、陈刚等[5]对Q235钢弹体撞击45号钢板后的破坏模式进行了实验和数值模拟研究，X.W.Chen等[6]还对金属玻璃基复合材料长杆弹对Q235厚靶的侵彻进行了实验研究，Y.F.Deng等[7-8]、张伟等[9]、郭子涛等[10]对单层和多层Q235钢板在不同弹体撞击后的防护性能和失效特性进行了实验研究。但到目前，国内关于Q235钢的断裂失效准则的研究报道并不多见，文献[5]根据部分实验数据给出了Q235钢的J-C本构和失效模型的近似选取参量，但失效模型中没有考虑温度软化效应;林莉等[11]对 Q235-B钢进行了详细的力学性能测试，给出了修正的J-C本构和失效模型，但实验中应变率范围较低，最大仅为275 s-1，其在穿甲冲击等高应变率问题中的应用有待进一步检验。

本文中使用Instron材料试验机、霍普金森拉杆(SHTB)对Q235钢试件进行不同温度下的准静态和动态拉伸实验，实验中应变率最大为2 854 s-1，研究温度、应变率及应力三轴度对Q235钢失效应变的影响，基于实验和数值模拟结果提出修正的Q235钢的J-C失效模型，并通过Taylor撞击实验与相应的数值模拟结果对实验给出的模型相关参量进行确定和验证。本文中所用的Q235钢材料均来自吉林通化钢铁有限公司生产的同一批次的3～20 mm厚钢板。

1 金属材料的J-C失效准则描述

金属材料的延性断裂与材料中空洞形核、扩展和聚合有关，而微孔洞的产生和增长与材料的应力状态即应力三轴度显著相关，温度和应变率对材料的断裂也有很大影响。G.R.Johnson等[1]考虑应力三轴度、温度及应变率效应,扩展了Hancock-Mackenzie的断裂模型形式[12-13]:

(1)

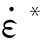
J-C失效模型利用累积损伤的思想考虑了应力状态、应变率及温度变化对材料破坏的影响，且认为损伤并不影响材料强度, 损伤变量初始值为0，当达到1时，材料即失效。单元的损伤演化定义为：

D=∑(Δεeq/εf)

(2)

式中:D为损伤变量，Δεeq为一个时间步的等效塑性应变增量。

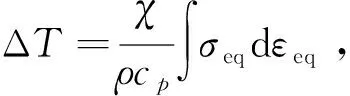
2 应力三轴度对失效应变的影响

主要通过对5 mm厚的平板缺口试件的单向拉伸实验，来考察应力状态即应力三轴度对失效应变的影响，缺口试件示意图如图1所示，通过对缺口拉伸试件的单向拉伸实验实现大于1/3的应力三轴度范围，通过对剪切试件的单向拉伸实现对中间部位的剪切，应力三轴度在0附近。缺口拉伸试件长度L=110 mm,d=10 mm保持不变,R分别为0.5、1.0、2.0、5.0和15.0 mm，对于光滑平板试件，R则视为无穷大, 剪切试件尺寸如图1所示。

使用万能材料试验机对试件进行准静态单向拉伸实验。实验后的试件如图2所示。利用有限元软件Abaqus/Standard分别建立了拉伸试样的三维轴对称模型和剪切试样的全尺寸模型，以试样中间断裂截面为研究对象，并按与文献[14-15]相同的方法，从模拟载荷位移曲线上找出N个与实验中具有相同位移时对应的载荷值和模拟位移，通过比较实验和模拟的N个载荷值大小以修正模拟中每个点对应的Misses应力，然后保持颈缩之前的应力应变不变，并加上修正后的N个点的等效应力应变再次进行数值模拟，依次反复迭代直到模拟得到的载荷位移曲线和实验结果十分逼近为止。平板试件的有限元模型及在发生颈缩时的Mises应力云图如图3所示，图4(a)～(b)分别为拉伸试样和剪切试样的实验和模拟的载荷位移曲线对比。

数值模拟中每个时刻的试样等效塑性应变取自试件断口截面上的所有单元的塑性应变平均值，当模拟的载荷位移曲线达到实验的断裂点时，试样等效塑性应变为试样的模拟断裂应变。由于现有的文献并没有关于平板缺口试件的应力三轴度的计算公式，因此每个缺口试样的应力三轴度随时间的变化由数值模拟获得。本文中每个试样的应力三轴度定义为自初始时刻到试样断裂时段内应力三轴度随试样等效塑性应变变化的平均值，文献[2,16]也采用了相同的处理方法。平均应力三轴度的计算公式表示为:

(3)

式中:σm表示静水压力，σeq表示等效应力即为数值模拟中的Misses应力。

本文中试样的断裂应变通过下式计算:

εf=ln(A0/Af)

(4)

式中:A0为试样最小截面的初始面积，Af为试样断裂时的断口面积。平板试样的断口形式近似如图5所示，本文中Af的计算由下式近似表示:

(5)

本文中尝试做了圆柱试件的准静态压缩实验，由于Q235钢延性较好，在试验机的最大量程范围内试样件没有出现裂纹，最大的塑性屈服应变经计算为1.8左右，应力三轴度的值为-1/3附近时的断裂应变暂时未知。剪切试样剪切断裂面的断裂应变值由于不容易测量计算，断裂应变值由数值模拟获得。图6所示为数值模拟得到的不同缺口试样的应力三轴度在断裂时刻内随等效塑性应变的变化，最终得到的失效断裂应变随应力三轴度的变化趋势如图7所示。

由图7可知，Q235钢的断裂应变并不随着应力三轴度的增大而单调递减，这与材料在不同应力状态下的破坏特性有关，在拉伸状态下，材料的断裂由材料内部孔洞形核、扩展、聚合造成，宏观上表现为韧性断裂破坏，在材料的剪切段时，材料失效主要表现为剪切破坏。Y.B.Bao等[2]对2024铝合金的研究以及陈刚[3]对TC4材料的破坏特性研究中也得出了相同的结论。采用与文献[3]类似的分段函数对图7中数据进行描述：

(6)

参数D1、D2、D3可以通过拟合拉伸段的数据获得，图中虚线圈标记的第1个点可以由拉伸段的拟合曲线外推至应力三轴度为1/3时获得，并结合剪切点确定D01和D03项，然后外推线性段至应力三轴度为0时，可以获得虚线圈标记的第2个点，第3个虚线圈标记的断裂应变应大于1.8。

3 应变率对失效应变的影响

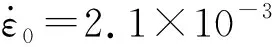
4 温度对失效应变的影响

以Q235光滑平板试件作为实验对象，进行了室温约900 ℃的准静态拉伸实验，图11所示为高温试件在不同温度下的断口形式，常温试件断口与100oC时相似而未列出，从图中可以看出，在温度为900 ℃时，试样内部材质发生物理变化而引起试样的不规则脆断，故断裂点本文中未予考虑。图12给出了试样的断裂应变随无量纲温度的变化，可以看出自常温到300 ℃时，断裂应变变化趋势不大，300～700 ℃时断裂应变随温度变化幅度增大。显然采用原始的J-C失效模型温度软化项(1+D5T*)并不能准确描述断裂应变随温度变化的趋势，本文中提出一个温度软化项为(1+D5T*D6)，采用原始的和修改的模型对图中数据的拟合效果如图12所示。通过拟合获得原始J-C模型温度项D5=3.811，而修改的J-C模型温度项D5=13.017，D6=2.338。

5 失效准则参量的Taylor实验和数值模拟验证

综上所述，可以获得基于J-C失效模型的修正形式：

(7)

除D02项外，失效模型参量其他项已全部获得。因为通过大应变率下的Taylor撞击实验是验证材料失效模型参数常用的方法[3,11]，故本文中开展了Q235钢的Taylor撞击实验，弹体取材于同一批次20 mm厚Q235钢板，名义直径和长度分别为12.62、50.48 mm, 屈服强度与先前测试的薄试样相同。实验结果发现撞击速度小于253.5 m/s时，弹体头部镦粗不发生开裂, 当弹体速度大于255.8 m/s时，弹体头部即由初始开裂发展为花瓣型开裂。利用Abaqus/explicit建立Taylor撞击实验的三维有限元模型，弹体和靶板的单元类型为C3D8R即八节点线性六面体单元，模型如图13所示, 弹体本构模型及参数通过同一系列实验得到[17]。由于裂纹发生在弹体头部，故弹体头部单元密度偏大。在失效模型其他项保持不变的情况下，调节D02项使得弹体速度在253.5 m/s时弹体头部只发生镦粗，当弹体增大到255.8 m/s时，Q235弹体头部发生临界开裂，如图14所示，此时获得的D02项值为-6.8, 这时准静态压缩时失效应变经计算为4.93。

为进一步验证Q235的本构和失效模型的正确及适用性，对Q235弹体在高速下的Taylor撞击实验进行了数值模拟，实验的和模拟的弹体花瓣型裂纹对比见图15所示，可以发现两者结果吻合较好，最终确定的Q235钢的失效模型相关参数如表1所示，其中:E为弹性模量,ν为泊松比,ρ为密度,Tr为参考温度,Tm为熔点,cp为比定压热容,χ为塑性功转热系数。

E/GPaνρ/(kg·m-3)Tr/KTm/Kcp/(J·kg-1·K-1)χε·0/s-12000.337 8002931 7954690.92.1×10-3D01D02D03D1D2D3D4D5D60.511-6.804.0470.47218.728-7.805-0.019 313.0172.338

6 结 论

对Q235钢试件进行了不同温度下的准静态和常温动态拉伸实验，研究了温度、应变率及应力三轴度对Q235钢失效应变的影响，结果表明，材料断裂应变随温度和应变率的增加分别呈递增和递减，同时由于Q235钢材料在不同应力状态下破坏机制不同，材料断裂应变随着应力三轴度的增加呈先减小后增大再减小的变化趋势。本文基于实验和数值模拟结果对失效应变温度项进行了修正，并提出了Q235钢的基于J-C失效模型的应力三轴度三分段式失效准则，最后通过Taylor撞击实验与相应的数值模拟对实验给出的模型相关参量进行了确定和验证，实验结果与模拟结果吻合较好。