概率分布假设检验中有效数据的重新分组

刘小宁 刘 岑 杨 帆 袁小会 陈 刚

(1.武汉软件工程职业学院 湖北 武汉:430205；2.湖北轻工职业技术学院 湖北 武汉:430070)

探索钢材机械性能参数的概率分布，是构建钢结构可靠性设计方法的基础工作[1]。

从概率论知识可知，钢材机械性能参数的概率分布应是对钢材机械性能参数无限有效试验数据的统计规律；从数理统计理论可知，工程界只能依据有限的有效试验数据进行假设检验，研究钢材机械性能参数概率分布[2-10]；因此，当有限的有效试验数据数量并不充足时，对其进行合理分组是涉及到假设与检验是否吻合的重要问题，即合理分组是关系到钢材机械性能参数的概率分布能否探索成功的关键[11-18]。

为此，文中基于概率论与数理统计知识[19-20]，在有限的有效试验数据数量并不充足时，对其进行合理分组进行研究，为探索钢材机械性能参数的概率分布提供思路。基于奥氏体不锈钢S30408超低温屈服强度的60组有效试验数据，对其概率分布进行了探索。

1 基本理论与方法

钢材机械性能参数的概率分布研究包括三个方面，一是机械性能参数试验数据的有效性，已在参考文献[2-4]进行了研究。二是机械性能参数的分布规律，当有限的有效试验数据数量充足时，其假设检验的基本方法见参考文献[1，6-10]；当有限的有效试验数据数量并不充足时，在假设检验时必须对其合理分组，如何合理分组是本文需要研究的重点。三是机械性能参数的分布参数，在已知机械性能参数分布规律的前提时，分布参数的计算方法已解决[1,19-20]。

当有限的有效试验数据数量并不充足时，以钢材机械性能参数R的正态分布假设检验为例，建立如下方法。

(1)当通过试验测得钢材机械性能参数R的n组有效试验数据Ri(i=1，2，…，n)时，其平均值与精密度分别为：

(1)

(2)

(2)假设R的分布规律。假设机械性能参数R是符合正态分布的随机变量。

(3)预分组并列表分组计算理论频数。根据有效数据个数n，把有效试验数据分为M个组[1]：

M=1+3.3lgn

(3)

并取整数。

正态分布随机变量R的有效试验数据Ri位于分组[a1，a2]，[a2，a3]，…，[aM，aM+1]内的理论概率为：

式中，φ(·)为标准正态积分；a1=(Ri)min，aM+1=(Ri)max，(Ri)min、(Ri)max分别为Ri中的最小值与最大值。

(4)

对于n个有效试验数据Ri，位于分组[aj，aj+1]内的理论频数为n×pj。

(4)列表试算分组的皮尔逊统计量并计算其之和。

第j个分组的实际频数Nj与理论频数n×pj差异的皮尔逊统计量为：

(5)

M个分组实际频数与理论频数差异的皮尔逊统计量之和为：

(6)

其检验条件为：若符合

(7)

则在显著度为δ时，假设成立，否则存在分组不合理导致检验不符合假设的可能，需要重新进行合理分组，然后再次检验。

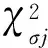
当重新分组后的组数为m，每组的实际频数与理论频数分别为Ni与n×pi，第i个分组的实际频数Ni与理论频数n×pi差异的皮尔逊统计量为：

(8)

m个分组实际频数与理论频数差异的皮尔逊统计量之和为：

(9)

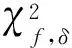
其检验条件为：若符合

(10)

则在显著度为δ时，假设成立，否则在现有条件下假设不成立。

本文取显著度δ=0.05，所用的χ2系数见表1[1,19]。

表1 χ2系数

显然，步骤(1)～(5)是现有的[1,14-15]，可称为预分组检验，步骤(6)～(7)是在预分组检验基础上补充完善，可称为重新分组检验。

2 算例

2.1 有效试验数据及其平均值与精密度

深冷容器常用奥氏体不锈钢S30408制造，通过试验，文献[5]获得了其屈服强度R在液氮温度(-196℃)时的60组试验数据，见表2，在双侧置信度为99%时这些试验数据都是有效的[8]。将有效试验数据代入式(1)与式(2)得到的其平均值与精密度一并列入表2。

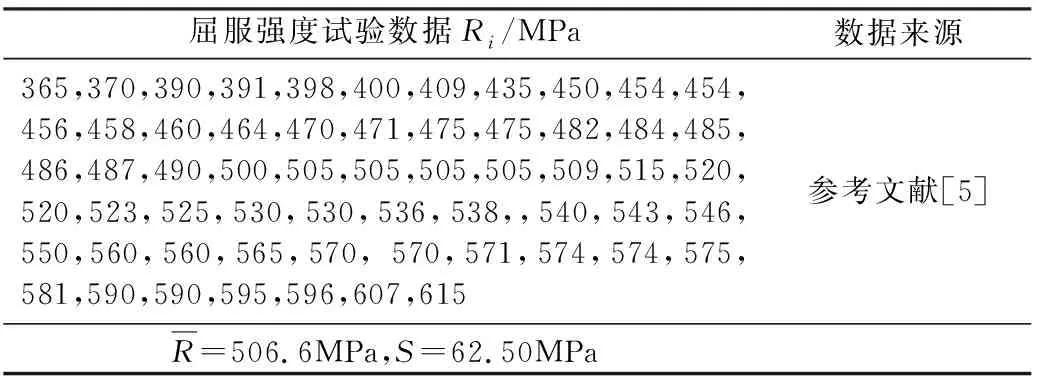
表2 奥氏体不锈钢超低温屈服强度的60组试验数据及统计

根据表2有效试验数据，可探索奥氏体不锈钢S30408屈服强度在液氮温度时的分布规律。

2.2 分布规律的两种假设检验方法

假设奥氏体不锈钢S30408屈服强度R屈服强度在液氮温度时符合正态分布。

2.2.1 预分组检验

对于60组有效试验数据，由于1+3.3lg60=6.87，因此将其分为7个组，每个分组的实际频数Nj、理论概率pj、理论频数n×pj、反映每个分组实际频数与理论频数差异的皮尔逊统计量及其之和见表3；7个组的自由度为F=7-1-2=4，取显著度δ=0.05，由表1可知，

2.2.2 重新分组检验

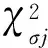
因此，可采用合并表3第1组与第2组的方法重新分组检验。重新分组后的组数m=6，第i个分组的实际频数Ni、理论概率pi、理论频数n×pi、以及反映每个分组实际频数与理论频数差异的皮尔逊统计量及其之和见表4。

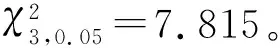
表3 预分组检验的皮尔逊统计量

表4 重新分组检验的皮尔逊统计量

3 讨论

3.1 预分组检验是重新分组检验的基础

预分组检验要求有效试验数据的数量必须充足，当数量不足时，某个分组的实际频数与理论频数可能会相差比较大，由式(5)与式(6)可知，该组的皮尔逊统计量与所有分组的皮尔逊统计量之和也大，会造成皮尔逊统计量之和不满足检验条件式(7)，解决此问题的方法有3个：

其一是在不增加有效试验数据的数量时改变假设再检验。

其二是在不改变假设，增加有效试验数据的数量后再检验。

其三是在不增加有效试验数据数量并且不改变假设时，基于预分组的计算结果，找出皮尔逊统计量大的分组，如果通过合并其相邻两组或者一组，达到减小实际频数与理论频数差异的效果，则重新分组，按式(8)计算每组的皮尔逊统计量，按式(9)计算所有分组的皮尔逊统计量之和，再按式(10)检验，若通过检验，表明假设成立。若不能通过，可按其一或者其二的方法处理。

比较上述三种方法可知，重新分组检验在技术上可行，在经济上较为合理。显然，重新分组检验不但以预分组检验为基础，而且是其补充完善。

3.2 重新分组检验对有效试验数据数量的最低要求

较多的有效试验数据对钢材机械性能参数概率分布的假设检验有利。当然，在满足要求的前提下，较少的有效试验数据数量在经济上更为合理。

由于重新分组检验的自由度f=m-1-2≥1，因此，重新分组的组数m≥4；考虑预分组组数在重新分组后至少减少了1，则预分组组数M≥5，由式(3)可得到重新分组检验对有效试验数据数量的最低要求：n≥17。

当然，对于预分组可通过假设检验的情况，要求分组组数M≥4，由式(3)可得到其对有效试验数据数量的最低要求：n≥9。

4 结语

1)针对数量有限的钢材机械性能参数有效试验数据，应用数理统计知识，在预分组检验的基础上，建立了重新分组的假设检验方法。

2)基于60组有效试验数据，利用重新分组假设检验方法可知，在显著度为0.05时，奥氏体不锈钢S30408在液氮温度时的屈服强度是基本符合正态分布的随机变量。