基于层次分析法的偿债能力综合分析

2018-10-15辛冰川

中国乡镇企业会计 2018年9期

辛冰川

引言

收入费用观到资产负债观的转变，凸显了资产负债表在财务报表体系中的核心地位。评价企业的偿债能力，有助于改善资产负债的管理，优化资产及资本结构，提高决策水平。然而在对企业的偿债能力进行分析时，面临的是一个由相互联系、相互制约的众多因素构成的复杂系统，各个单因素指标只能从某一方面反映企业偿债能力，很难从总体上做出全面的、客观的结论。特别是指标体系中各指标好坏不一致时，更是如此。层次分析法特点是把复杂决策问题的有关因素层次化、数量化，用数学的方法为分析决策提供定量的依据。

一、层次分析法的介绍

层次分析法（analytic hierarchy process,AHP）是美国著名的运筹学家T.L.Satty等人在20世纪70年代提出的一种定性与定量相结合的多准则决策方法。层次分析法通过两两比较的方式确定层次中诸因素的相对重要性，然后综合决策者的判断，确定决策方案相对重要性的总的排序。

1.设计评价指标并建立层次结构

选择合理的评价指标评价企业偿债能力的基础，本文以客观性、合理性、可操作性等原则为指导思想，选取了企业的发长期偿债能力、短期偿债能力、营运能力、盈利能力四个方面分析评价企业的偿债能力,每一方面又细化为若干指标。同时构建层次分析结构模型，以使得问题条理化，层次化，如下图1-1所示：

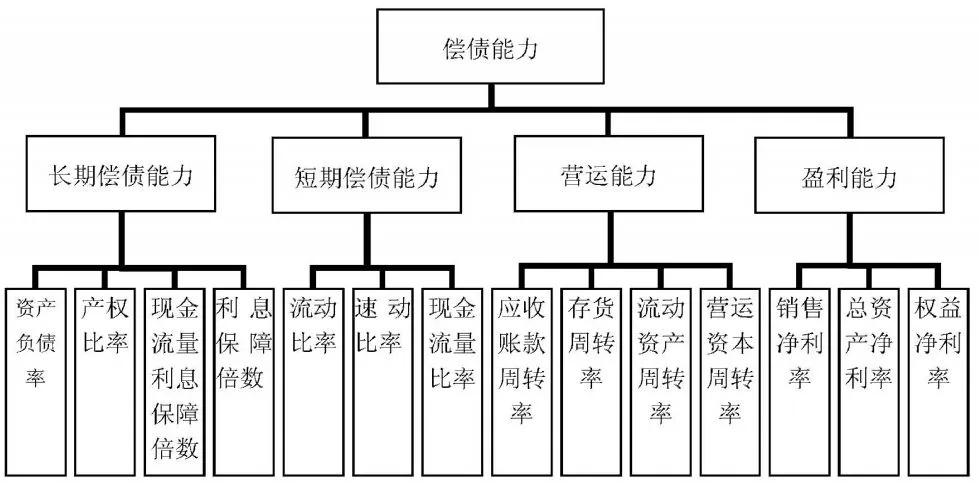
2.构造判断矩阵

建立层次分析模型之后，就可以在各层元素中进行两两比较，构造出比较判断矩阵。

判断元素的值反映了人们对各种因素相对重要性的认识，一般采用1-9标度及其倒数标度方法。两个元素进行比较，两元素同等重要时取值1，一个元素比另一个元素稍微重要取值3，明显重要取值5，强烈重要取值7，极端重要取值9。两个元素比较判断需要折中时采用2、4、6、8。

3.层次单排序及其一致性检验

具体地说，层次单排序是指根据判断矩阵计算对于上一层某元素而言本层与之有联系的元素重要性次序的权值。理论上讲，层次单排序计算问题可归结为计算判断矩阵的最大特征根及其特征向量的问题。

4.层次总排序

计算各层元素对系统目标的合成权重，进行总排序，以确定结构图中最底层各个元素在总目标中的重要程度。

二、层次分析法的应用

下面，以A公司为例进行发展能力分析。A公司最近二年的相关指标数据如下：

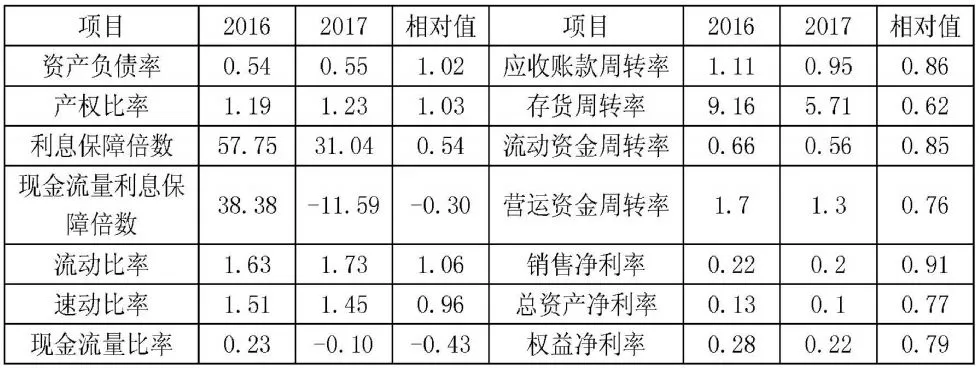
1.建立层次结构，如图1-1

2.构造判断矩阵，并对各判断矩阵的各层次单排序进行计算及求得一致性检验结果

（1）准则层对目标层判断矩阵

准则层权重的计算的结果及一致性检验的结果是：

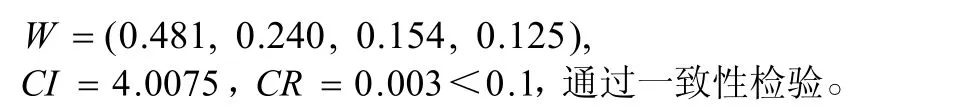
（2）目标层对指标层判断矩阵B-C

目录层权重的计算结果及一致性检验的结果是：

3.第三层指标权重（层次总排序）为：

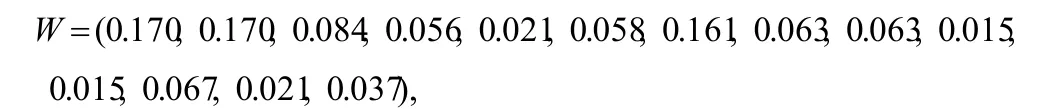
4.最后利用各项单一指标数值与对应的权重相结合，对公司的偿债能力进行整体全面评价。可将2016年指标数值作为基期数据，通过计算2017年的相对值并与权重相结合，综合量化评价偿债能力的变动幅度。

0.17×1.02+0.17×1.03+0.084×0.54+0.056×-0.30+0.021×1.06+0.058×0.96+0.161×-0.43+0.063×0.86+0.063×0.62+0.015×0.85+0.015×0.76+0.067×0.91+0.021×0.77+0.037×0.79=0.61

2017年由于经营活动现金流量为负值并且大部分偿债能力指标较2016年均有所降低，2017年A公司偿债能力较2016年下降了39%。需要提请注意的是，由于不同行业的偿债能力指标值通常有明显的的差别，不存在统一、标准的比率数值。所以还应针对目标公司的具体经营情况并参照本行业的参考值对指标进行标准化处理，以规范偿债能力综合评价的科学性。