基于时间最优控制的起重机防摆控制技术研究
2018-10-15宋劲松张明哲
宋劲松, 李 凌, 张明哲
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
起重机利用绳索一类的柔性体代替刚体工作,以使得起重机的结构轻便、工作效率高.但是采用柔性体吊运也带来了一些负面影响,例如起重机负载的摆动一直是困扰提高起重机装运效率的一个难题.在码头、仓库等货物集散地,龙门起重机系统必须快速平稳地吊运货物,吊运过程中,重物摆角幅度不能太大,在平稳停车后,重物摆角要尽快归零,到达稳定状态,以便进行下一步运输.研究龙门起重机更加快速地消除摆动、提高运行效率具有重要的现实意义.
对于龙门起重机的防摆问题,人们进行了数十年的规范研究.早在上世纪末,受限于当时技术和材料,龙门起重机的设计偏于保守以保证安全性,设备通常非常笨重,以较慢的运行速度降低货物摆动,工作效率低下.新世纪初,随着工业的快速发展,远洋物流运输速度不断加快,这对龙门起重机的性能有了新的要求,在保证安全和稳定的前提下,需要有更高的转运速度,龙门起重机迎来了新的发展,新技术新方法被普遍运用.其中,创新的控制技术在起重机防摆研究中起着至关重要的作用,PID参数优化、内模控制、模糊控制等控制技术的应用使龙门起重机消摆问题得到一定程度的优化[1].
控制系统的目标是以最小的过冲和最大的速度将货物移动到龙门起重机上一个新的位置.大多数龙门起重机控制系统,以提高系统稳定性和鲁棒性为主要目标,而更快的转运速度则是行业领先的标杆.相较于传统的控制方法,应用时间最优控制能够在系统稳定基础上最大程度地提高运行效率.本文对龙门起重机系统进行建模,结合时间最优控制原理,在摆动允许范围内,实现最快速的运行,并通过Matlab仿真验证方法可行性.
1 时间最优控制问题
最优控制问题是从事研究工作人员经常碰到的问题,应用什么样的技术手段使人们能够用最小的花费得到最好的效果是研究的重点[2].
1.1 时间最优控制问题的数学描述
受控系统的状态方程可以表示为:
(1)
给定的终端状态为x(tf)=xf,对控制变量的约束为u(t)∈U∈Rr.
若选择允许的最优控制函数u*(t),其将使得系统的状态方程从初始状态x0出发,转移到终端状态xf的过程所需要的时间最短(即(tf-t0)=tmin),称这一问题为时间最优控制问题[1].
时间最优控制问题的性能指标函数可表示为:
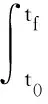
(2)
1.2 时间最优控制的必要条件
根据极大值原理可知,线性系统的时间最优控制有解的必要条件是:控制域U必须是“有界闭集”,且最优控制函数必定取这个闭集U的边界值。由此可得出时间最优的控制为:
(3)
由此可见,允许控制的时间最优控制系统是Bang-Bang型(也称砰砰型)控制系统,只有继电型非线性系统才能实现时间最优控制[1-2].
2 系统建模
2.1 模型建立
龙门起重机问题为多刚体、多自由度、多约束的质点系动力学问题.在生产生活中龙门起重机模型实际上是一个三维模型,但是龙门起重机在运动过程中,主要受力情况分布在二维空间内,在另一个维度方向上受力主要是一些扰动(比如风力).为了研究方便,将实际的三维模型抽象成二维模型,且在龙门起重机运行过程中认为绳长不变,缆绳的质量相对于重物的质量可以忽略不计.模型如图1所示[3].

图1 起重机系统的物理模型
重物通过绳索与小车相连,小车在电动机的水平拉力F1的作用下在平直轨道上运动.小车的质量为m0,重物的质量为m,绳索的长度为l,可在提升电动机的提升力F2作用下进行升降运动,重力加速度为g;绳索的弹性、质量、运动的阻尼系数可忽略;小车与水平轨道的摩擦阻尼系数为D;重物摆动时的阻尼系数为η,其他扰动可忽略[4].取小车位置为x1,绳长为x2,摆角为x3,将它们作为系统的广义坐标系,在此基础上对龙门起重机系统进行动力学分析建模.其中,所涉及的参数、变量、单位及取值参见表1.

表1 参数变量表
由图1所示的坐标系可知,小车和重物的位置坐标为:
(4)
所以小车和重物的速度分量为:
(5)
系统的动能为:
(6)
此系统的拉格朗日方程组为:
(7)
(8)
2.2 模型简化
为了应用经典控制理论分析所建立的系统,就需要把式(8)所示的非线性方程组进行线性化处理[5].
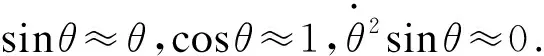
(9)
对式(9)进行拉普拉斯变化可得:
(10)
式(10)即为系统的传递函数模型形式,据此可以得到图2所示的定摆长起重机运动系统动态结构图,图3是其另一种表达形式.
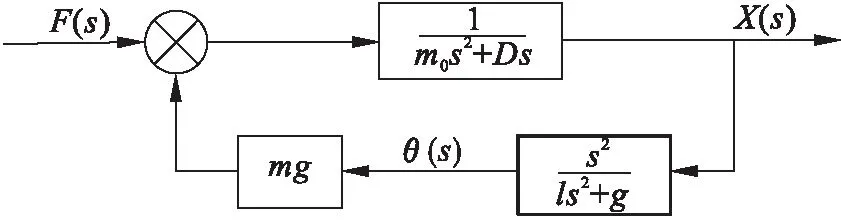
图2 定摆长起重机运动系统动态结构

图3 变换后的定摆长起重机运动系统动态结构
同理,也可将上述模型转化为状态空间形式.对式(10)进行变换,每个式子只保留一个二次导数项,可得:
(11)

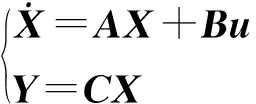
(12)
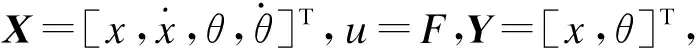
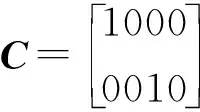
(13)
在摆长一定的情况下,起重机模型的状态空间表达式即如式(13)所示.
3 应用时间最优控制策略
由于起重机防摆控制问题的核心是在有效消除重物摆动的条件下,使小车能够快速可靠定位,可以通过对重物摆动规律分析,选定有效的控制策略[6-7].
3.1 负载重物摆动问题的数学描述
在建立了龙门起重机的整体运动模型后,为了应用时间最优控制方法,还需要对负载摆动模型独立进行分析.
(14)
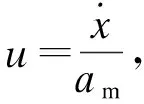
这样负载的摆动方程可以写成:
(15)
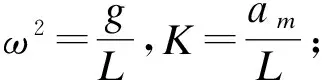
(16)
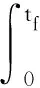
3.2 摆动规律相平面分析
为实现有效控制需要研究重物的摆动规律,通过相轨迹对摆动进行分析比较容易,这里应用相平面分析法.
重物摆动的状态方程对应的状态转移矩阵为:
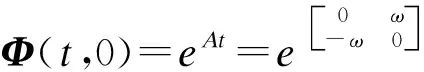
(17)
其解为:
(18)
为了使时间最优,取控制规律u(t)=Δ(Δ=±1,0),并设ωx1(t)、ωx2(t)为新的状态,式(18)可整理为:
[ωx1(t)-Δ]2+[ωx2(t)]2=
[ωx1(0)-Δ]2+[ωx2(0)]2
(19)
龙门起重机系统负载摆动的相平面图如图4所示,其中,Dx=ωx2(t)为纵坐标,x=ωx1(t)为横坐标.

图4 系统相平面
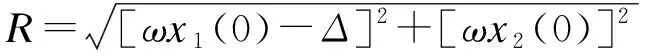
3.3 消摆控制策略
通过前面的分析,可以得到龙门起重机的运动规律:启动时u(t)=1,加速度处于最大,重物的摆动状态对应图5中的右半平面的实线;当状态运动一周回到原点,此时摆角及摆速均为零,加速为零,小车处于匀速运动状态,摆动消除;同理,当制动停车过程中,始终以最大减速度减速,即u(t)=-1,重物的摆动状态对应图5中的左半平面虚线;当状态运动回到原点时,减速停止,摆动消除[6].
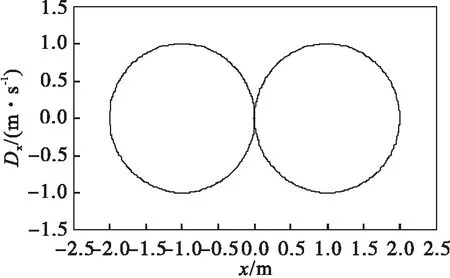
图5 当u(t)等于-1和1时的相平面图
该消摆控制策略加减速的时间ts相同,均为走完一个完整圆周使用的时间,即有:
由此可知,负载摆动具有周期性,且只需控制小车的加速度就能控制摆动幅度.控制器可以通过改变输出PWM占空比将加速度信号转换为伺服驱动器可以接收到的速度信号.所以,控制器只需要设计为开环就能满足需要.其控制结构框图如图6.操作人员发送控制信号给控制器,控制器接收到控制信号给出的位置坐标,根据已知的绳长及其他限制条件计算出加速度的时间序列,最后发送给小车伺服驱动器驱动小车进行工作.
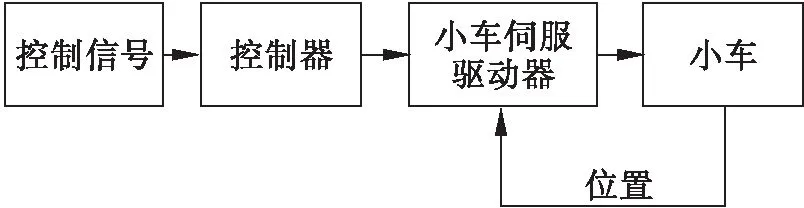
图6 起重机控制结构框图
假设起重机的启动制动最大加速度为am,最大速度为vm,绳长为l,要行走的距离为s.下面给出消摆的切换时间序列.
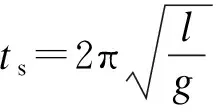
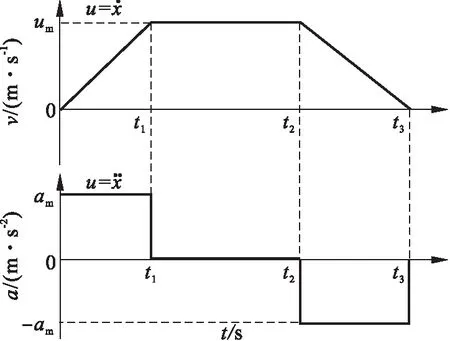
图7 起制动切换时刻
4 仿真实验及结论
4.1 实验结果
综合以上分析,建立如图8所示仿真结构,其中控制器输出为图7计算的加速度时间序列,并通过增益输出力作用于所建立的起重机动力学模型,继而输出仿真结果,如图9所示.
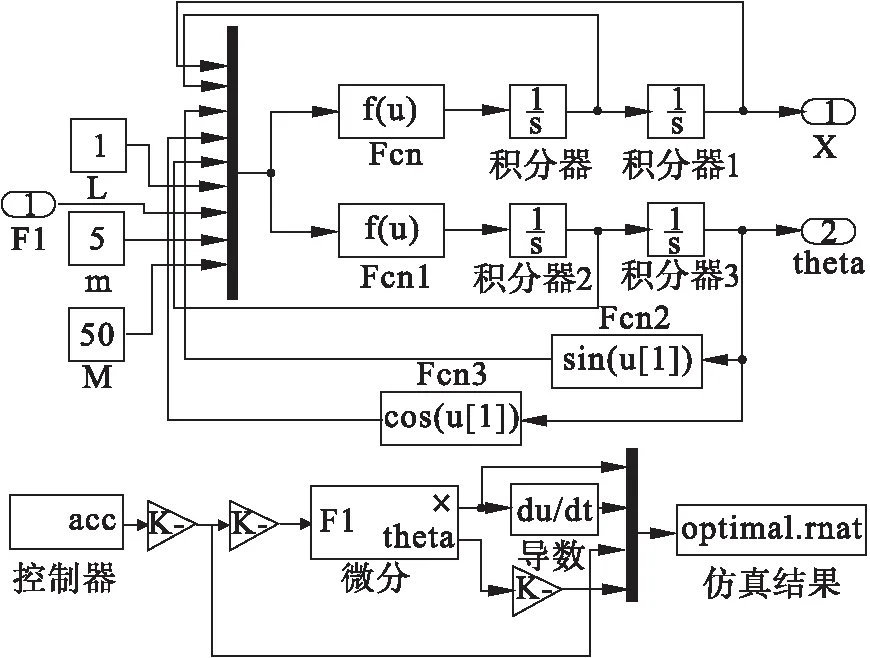
图8 Simulink仿真框图
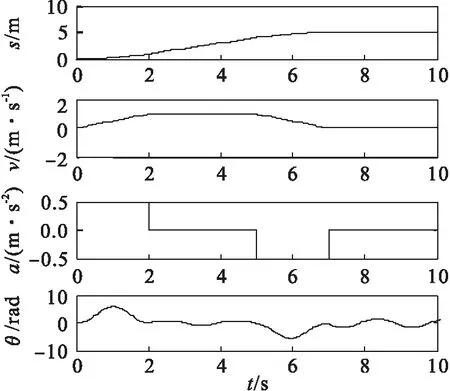
图9 系统仿真结果
由图9得知:重物摆动幅度在控制在很小的范围内(|θ|<10 rad)时,经过时间最优控制的龙门起重机模型在最大速度运行的情况下有良好的消摆效果,这也验证了之前的理论推测.
4.2 实验结论
(1) 实验设计基于时间最优理论.根据上节的实验结果,摆角绝对值小于10 rad,在满足理论最大运行速度的前提下,符合预期消摆要求.所以,实验证明了所设计的基于时间最优控制的起重机防摆控制方案是可行的.
(2) 相较于其他控制方法,时间最优控制在实际的龙门吊防摆应用中具有诸多优点,如不需要检测摆角、运行速度快、控制较为简单等.
(3) 时间最优控制在防摆应用中也有其不足,比如要求摆角初始为零.此外,实验实质为开环控制,实现更加精确的控制还需要在控制器中加入角度位置等反馈控制.
