基于近邻距离加权主元分析的故障定位

郭小萍, 李克勤, 李 元

(1.沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)

随着现代工业的快速发展，为保证工业生产的安全、高效，工业过程监视与故障诊断变得越来越重要.在现代复杂工业过程中，由于集散控制系统的应用，获取了大批次的生产过程数据，使得基于数据驱动的过程状态监视与故障诊断成为研究热点[1-3]，故障定位也得到了越来越多的关注和重视.

对于多元统计过程监视最常用的方法为偏最小二乘(Partial Least Square，PLS)法[4-5]与主元分析(Principal Component Analysis，PCA)法[6-7].其中PCA法将工业生产过程在正常条件下产生的原始高维数据进行数据特征提取并降维，建立监视模型，得到控制限.若检测样本的监视统计量超过该控制限，就认为此刻发生故障[8].在检测到过程故障后，可以通过定位的方法确定引起故障的变量，找出故障源.对于故障定位，贡献图分析法是最常用的一种方法，通过求待测样本各个变量对监视统计量的贡献值并做出柱状图进行对比分析，认为贡献值大的变量为故障变量[9].Alcala C F等人[10]提出了一种重构贡献法，可以明显提高单变量故障的诊断效果.但做贡献图分析时，由于变量之间的相互影响，导致非故障变量的贡献值变大，引起拖尾效应，容易造成误诊.Van等人[11]运用数值例子对重构贡献(Reconstruction Based Contribution，RBC)法产生的拖尾效应进行验证分析.叶昊等人[12]考虑了不同变量间贡献值的影响，将权值的概念引入到RBC法，提高了诊断效果.LIU J L等人[13]提出了一种基于改进贡献图(Modified Contribution Plot，MCP)的故障定位法，将所有检测样本的各个变量的贡献值作出矩阵图，可以连续直观地体现出连续过程所定位出的故障变量.但是该方法并没有改善PCA本身存在的检测率较低的缺点.

本文提出了一种加权PCA故障定位方法.对正常工况样本进行加权，强化正常工况变量特征，以加权后的样本建立PCA模型，计算并确定过程监视综合统计量[10]及其控制限，判断是否发生故障.对故障发生时刻的变量采用改进重构贡献(Modified Reconstruction Based Contribution Plot，MRBCP)法[14]进行故障定位，对每个变量进行逐个重构、检测，反复迭代分析，直至所有发生故障的变量被定位出来.最后通过仿真实验研究，与基于PCA的MRBCP方法进行比较，该方法降低了漏报率，并能准确定位出所有故障变量.

1 基于主元分析的故障定位

1.1 主元分析

(1)

(2) 计算X的协方差矩阵RX，X为标准化处理后的矩阵.

(2)

(3) 求解协方差矩阵RX的特征值λ与相对应的特征值向量p，λi是RX的第i个特征值，假设满足λ1≥λ2≥…≥λn，pi是对应于λi的特征矢量.

|λI-RX|=0

(3)

|λiI-RX|pi=0,i=1,2,…,n

(4)

(4) 根据累计贡献率选择相对主元个数，累计贡献率常取85 %.

(5)

其中，k为选取的主元个数.

1.2 过程监视统计量

将矩阵X分解成式(6)所示.

(6)

(7)

(8)

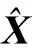
1.2.1 HotellingT2统计量

T2统计量的计算公式[1]为

T2=XPΛ-1PTXT=XDXT

(9)

式中，Λ表示由前k个特征值构成的对角阵.

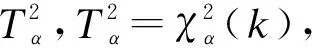
1.2.2SPE统计量

SPE统计量的计算公式[1]为

SPE=X(I-PPT)XT

(10)

采用核密度估计方法求得SPE统计量的控制限SPEα.

1.2.3φ统计量

φ统计量的计算公式[1]为

(11)

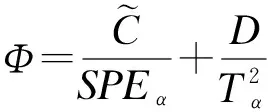
(12)

控制限φα为

(13)

其中：

(14)

(15)

(16)

(17)

1.3 重构贡献法

当故障发生时，对于单变量发生的故障，故障变量x可以分为正常部分和故障部分，如式(18)所示:

(18)

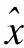
yi=x-ξifi

(19)

由式(19)可以得到重构变量yi的监视统计量:

(20)

式中，M为矩阵代号，当M=PΛ-1PT时，计算的是T2统计量; 当M=I-PPT时，计算的是SPE统计量; 计算综合统计量时，M=Φ.

通过使重构样本的监视统计量D(yi)最小，可获得故障幅值fi，对式(20)求偏导:

(21)

得到幅值公式:

(22)

在进行故障定位时，当定位的故障方向ξi准确时，重构样本监视统计量D(yi)会低于控制限φα，若高于控制限则表示定位不准确.

重构贡献率最大时所对应的变量为故障变量.重构贡献率为单个变量重构贡献值所占的比重.单变量的重构贡献值计算如下:

(23)

对于多变量发生故障时，多变量的重构贡献值为[17]:

cRBC=xMΞ(ΞTMΞ)-1ΞTMxT

(24)

式中，Ξ为故障方向构成的矩阵.如果变量x3、x6为故障变量，则其故障方向矩阵为:

(25)

进行定位时，需要求出对应的故障方向矩阵Ξ，使RBC值最大，若Ξ定位不准确，则RBC值会较小.

2 基于近邻距离加权PCA的故障定位方法

2.1 基于样本最近邻距离的加权方法

正常工况下的样本进行标准化之后，要进行加权运算，采用样本间的相似性特征强化正常样本的特征.加权因子的选择有多种方法，本文提出一种将正常样本间欧氏距离作为加权因子的方法，如式(26)所示.

(26)

式(26)中d为m×m的各个样本间欧氏距离矩阵，取每个样本与其最近样本的距离，设每个样本与其最近样本间的距离构成的向量为W，则定义正常样本加权变换矩阵为:

XW=diag(W)·X

(27)

式(27)中，XW为加权后的矩阵，可以采用PCA方法对XW进行分析，建立加权PCA监视模型.

2.2 加权PCA监视模型的建立

过程监视模型的建立过程如图1所示.

详细描述如下：

(1) 采集正常工况下的样本构成样本集X*;

(2) 采用Z-score标准化法对X*进行标准化处理为X;

(3) 求X中各个样本间的欧氏距离，将最近邻距离对样本进行加权处理为XW;

(4) 对XW进行PCA分析，建立加权PCA监视模型;

(5) 根据式(11)计算统计量φ建模;

(6) 根据式(13)及φ建模确定控制限φα.

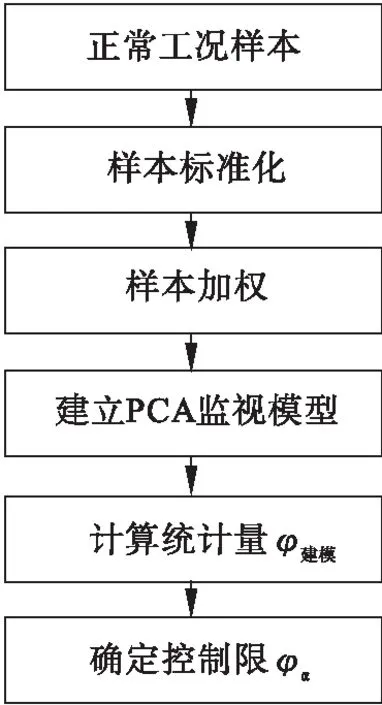
图1 过程监视模型流程图

2.3 过程监视与故障定位

对于实时采集的样本，其过程监视与故障定位的流程如图2所示.

图2 过程监视与故障定位流程

详细描述如下:

(1) 对于检测样本，采用建模样本的均值和方差对其进行标准化处理；

(2) 采用建模样本间的最近邻距离进行加权处理；

(3) 利用加权PCA模型计算检测样本的统计量φ检测；

(4) 判断φ检测是否高于控制限φα，若高于，则进行(5)；反之，则采集下一样本；

(5) 定义一个空集Xf=φ作为故障变量集合，故障变量的个数定为0，暂未定位的变量认为非故障变量;

(6) 将Xf与变量1(第一个非故障变量)组合；

(7) 求出该组合的最大RBC值，并将其对应的变量加入Xf;

(8) 利用式(20)计算Xf的重构监视统计量D(y)，式(20)中取M=Φ，判断D(y)是否低于控制限φα，若低于则进行(10)；

(9) 反之，则将Xf中的故障变量与下一个未被定位的非故障变量组合，回到步骤(7)继续循环定位; 依次迭代.

(10) 求各变量的贡献率，做出贡献图，完成定位.

3 仿真研究

3.1 数值案例

设数值案例有20个变量xi,i=1,2,…,20，该过程模型[18]为:

x=Gt+e

(28)

xf=x+Ξf

(29)

式中，Ξ为多变量故障的方向向量构成的矩阵，f为故障幅值，从第100个样本开始，对3个变量x1、x8、x18都加一个幅值f=2的故障.

基于加权PCA的MRBCP方法应用于数值例子的故障定位分析如图3所示.横纵坐标分别表示样本检测时刻和变量，彩色带表示重构贡献率，重构贡献率大的变量则被认为是故障变量.

从图3可以明显看出在100时刻之后，变量x1、x8、x18的重构贡献值明显较大，3个故障变量能够清晰准确地被定位出来.

图3 加权PCA法应用于数值案例的贡献图

3.2 TE过程仿真

TE(Tennessee Eastman)过程是一个对TE化学公司实际生产装置的真实模拟，是一个典型的多变量连续复杂过程，被广泛应用于过程故障诊断[19].TE过程包括5个主要操作单元:反应器、冷凝器、循环压缩机、气液分离器、汽提塔；包含8种成分:A、B、C、D、E、F、G及H.该过程有12个操纵变量和41个测量变量，其中41个测量变量包括19个成分测量变量和22个连续过程测量变量.现对22个连续过程测量变量进行研究.TE过程有20个故障类型，采用的建模样本由正常工况下22个变量的500个采样构成；采用的检测样本由故障工况下22个变量的960个采样构成，对故障1和故障14进行试验.故障1[20]和故障14[14]的故障变量如表1，并且均从160时刻发生故障.

表1 故障变量

为了验证加权方法对样本产生的影响，作出加权前后的样本分布图进行比较.图4是建模样本160～500时刻的分布图，图5是故障1的检测样本160～960时刻的分布图.由图可以看出样本加权之后，样本分布范围虽然被整体放大，但是样本间分布却更加紧密，放大了变量的个体特征，降低变量之间的相互影响，可以使变量被逐个定位时更加准确.

图4 建模样本分布图

图5 监测样本分布图

基于PCA的MRBCP方法、基于加权PCA的MRBCP方法对TE过程故障1的故障定位分析如图6、图7所示.故障发生初期，即160时刻到大约400时刻，由于各变量之间的相互影响，无法准确定位出故障变量.400时刻以后，由于控制系统的调节，可使系统达到新的稳定.从图6可以看出基于PCA的MRBCP方法只能定位出一个故障变量，而图7基于加权PCA的MRBCP方法可以准确定位出所有故障变量，大大降低了漏报率.同时，降低了非故障变量对故障变量的影响，避免了定位出非故障变量的误报情况，定位结果明显、准确.

图6 故障1基于PCA方法的贡献图

图7 故障1基于加权PCA方法的贡献图

基于PCA的MRBCP方法、基于加权PCA的MRBCP方法对TE过程故障14的故障定位分析如图8、图9所示.虽然基于PCA的MRBCP 方法对于故障14也能准确定位出所有故障变量，但是可以明显看出在发生故障时刻之后，并不是每一时刻都可以检测到故障，有较高的漏报率.而采用加权PCA的MRBCP方法时，发生故障后，每一时刻都可以检测出故障，降低了漏报率.故障1在400时刻之后的漏报率如表2所示.故障14在400时刻之后的漏报率如表3所示.

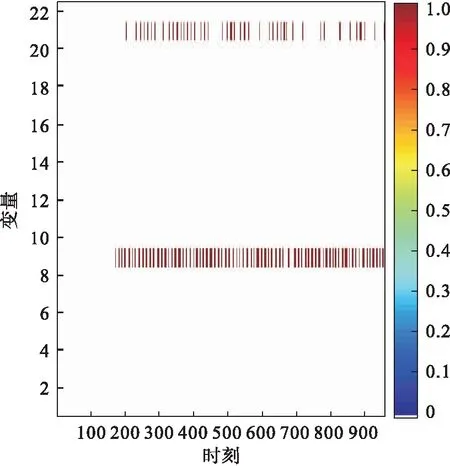
图8 故障14基于PCA方法的贡献图

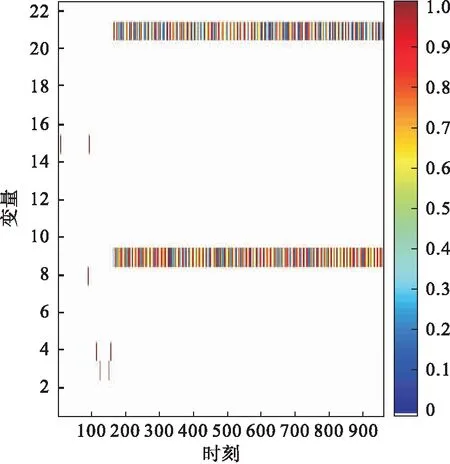
图9 故障14基于加权PCA方法的贡献图

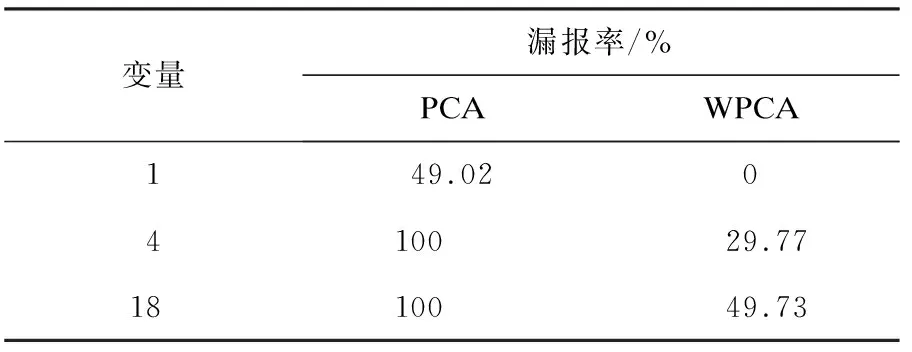
变量漏报率/%PCAWPCA149.020410029.771810049.73

表3 故障14漏报率对比表

为了进一步验证所提方法的正确性，在式(24)中，将每个故障方向(Fault Direction)向量逐步加入故障方向矩阵Ξ.以故障14为例，图10为故障14的逐步重构监视结果.可以看出在160时刻后，原始样本的监视值高于控制限，加入一个故障方向向量进行重构后，监视值更接近控制限.直至所有故障变量加入故障方向矩阵中，重构样本的监视值低于控制限，说明所有故障变量都被重构为正常变量，即所有的故障变量被定位出来，验证了被定位故障变量的准确性.

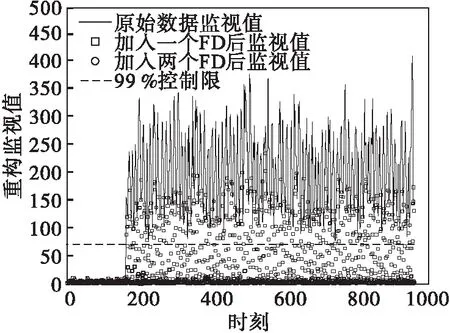
图10 故障14逐步重构监视结果

4 结 论

提出了一种将正常工况下样本间最近邻距离作为加权因子对样本进行加权的方法，采用综合统计量作为监视统计量，在多变量发生故障的情况下，与基于PCA的改进重构贡献图的故障定位方法进行对比，所提方法定位准确并降低了漏报率.但是，该方法通过对贡献率的大小判断变量是否发生故障，忽略了贡献率低的变量，其是否为故障变量仍需进一步研究.