分离器入口处不同形状挡板对内部流场影响的比较分析
2018-10-15王学平吴剑华
王学平, 文 学, 龚 斌, 吴剑华
(沈阳化工大学 机械工程学院, 辽宁 沈阳 110142)
液液重力沉降器具有分离效果好,能源消耗少,操作简单,没有二次污染的特点[1],所以被广泛的应用于分离互不相容的两相液体.分离器内部流场的稳定性对分离效果具有十分大的影响,分离器内部流场的理想流动状态是稳定的层流甚至柱塞流.而从入口处进入的液体往往具有很大的动能和湍动,对内部流场造成猛烈的冲击,容易引起分离器内部流场发生剧烈的扰动和漩涡,十分不利于液滴的沉降和聚结,因此,需要在分离器的入口处设置防冲挡板来消能和稳定流场,使防冲挡板后面分离区的流场尽量减少、减小漩涡和波动,并使流体流速在流场中的分配尽量均匀,尽量接近理想的有利于分离的层流状态[2].而防冲挡板的形状和大小以及与入口处的距离对内部流场稳定性的影响有着不同的效果,因此,有必要针对这些因素进行研究,以找出有利于流场稳定的配置形式.目前,防冲挡板的主要形式有板状、碟型、离心式和孔箱式.对于液液分离器入口构件的研究,各学者对陆耀军等[3]1995年提出的几种观点引用至今,但其仅通过查看单一条件下分离器内部速度矢量图后便定位挡板作用好坏,未对其他状况进行详细的对比研究;而国内外其他学者都是在假定分离器内部流场稳定的条件下,研究分离效率[4-7];有的学者直接忽视湍流冲击,将入口冲击射流速度通过面积比换算成整个分离器截面的速度,即视进液为层流状态,没有充分研究对保证分离区流场流动稳定起决定作用的防冲挡板的影响.平板式和球壳式(碟式)因结构简单,效果较好,被广泛应用于沉降式分离器中,但目前针对球壳式(碟式)挡板及其与平板式挡板在各种配置下的比较研究较少,对于这两种挡板在相同配置变化下对流场的不同影响未知,造成选型时的盲目性.因此本论文利用FLUENT软件针对这两种常用的防冲挡板变化相同的入口流速、形状尺寸、挡板与入口距离,对分离器内部的流场速度分布、平均速度及平均湍流强度的影响进行对比分析,为分离器防冲挡板的设置和选择提供依据.
因为分析的是对分离有很大影响的流体整体的流动状态,而一般情况下分散相液滴相对于连续相所占的比例较少且相对于连续相为轻相,对以连续相为主的流体整体的流动性影响可以忽略不计,因此,本文采用单一介质的形式进行模拟.
近年来,一种新型的计算方法—CFD(Computational Fluid Dynamics)成为研究各种流体流动状态的有效方法[8].CFD在构建理论和模拟流体流动的模型上可以做出准确的预测和决断,相比于研究性实验,它最大的优点是节省了实验成本,只需通过操作计算机进行模拟,便可快速得到理想的结果.CFD模拟出的结果并不是来自于实际模型的结果,而是来自于数学模型的结果,虽然是在理想状态下进行模拟,但并不会与实际情况产生特别大的偏差.集众多优点于一身的CFD计算方法正在日益完善,在工业生产与工业设计中得到了极为广泛的应用.
1 数值模拟
1.1 物理模型
由于只研究防冲挡板的作用,而不研究分离过程,为更好地反映防冲挡板的作用,所以简化掉挡板后的内部分离构件等结构.本文两个模型结构与尺寸参数如图1所示.水槽长×宽×高=1 400 mm×400 mm×400 mm(不包括进液管和排液管长度),进液圆管建立在前壁面上,圆心高度为150 mm,直径60 mm,溢液板高度为300 mm,进液管和排液管长度均为30 mm.流体由进液管进入分离器,由排液管流出.
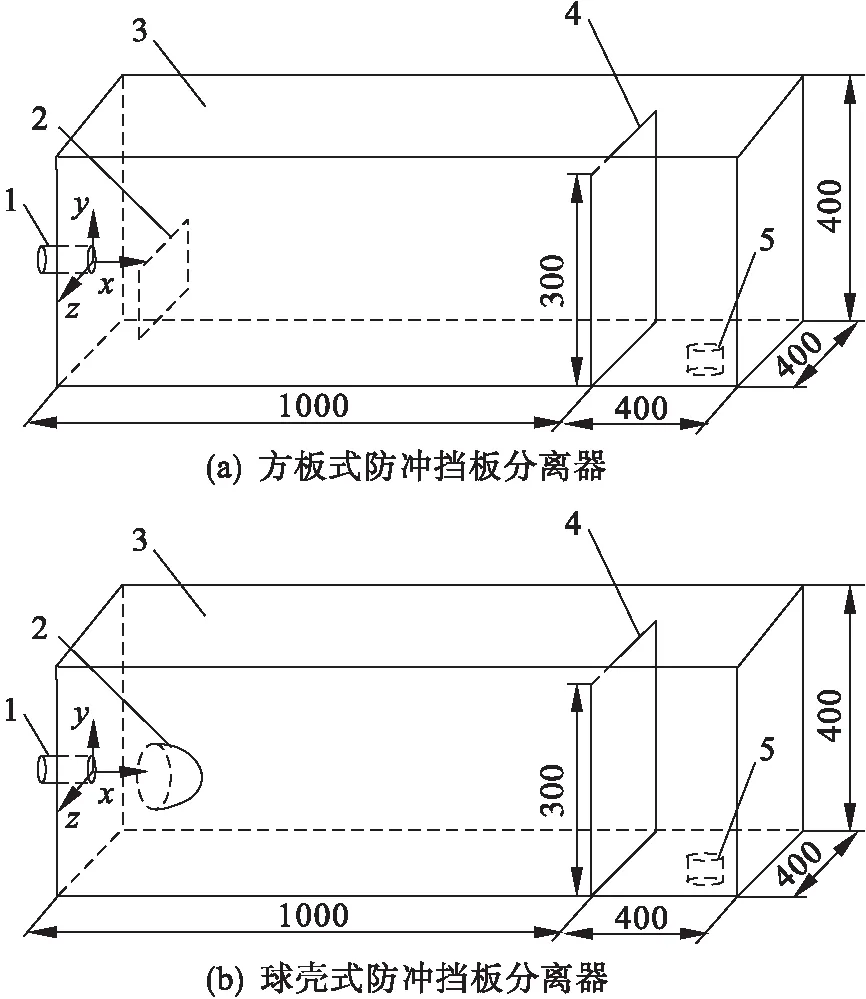
1 进液圆管 2 防冲挡板 3 分离器箱体 4 溢流板 5 排液管
模拟数值设定:根据对实际分离器入口流速和对流场稳定性效果影响的显著性的考虑,在做了多组模拟后,本文选取其中的v1=0.5 m/s、v2=1 m/s、v3=2 m/s三个冲击射流速度,在考虑实际流速的基础之上,具有一定的广度.H取H1=200 mm、H2=250 mm、H3=300 mm、H4=350 mm和H5=400 mm五个冲击间距,球壳挡板的直径和方形挡板的边长取Ф1=D1=80 mm、Ф2=D2=120 mm、Ф3=D3=160 mm、Ф4=D4=200 mm,用符号S表示4个防冲挡板尺寸.模拟参数组合见表1.
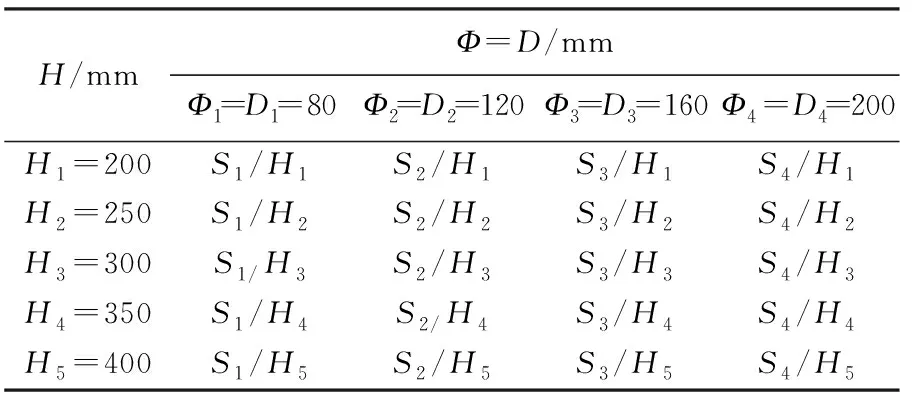
表1 模拟数值设定
1.2 网格无关性验证
三维几何模型用Gambit软件生成,采用非结构四面体网格进行网格划分,并对分离器前部主要研究区域进行网格加密.为保证计算精度,选取参数为v2=1 m/s、H2=250 mm、Ф3=D3=160 mm时的网格疏密程度进行6套网格考核验证.图2为6套不同网格尺寸在挡板冲击区取边长为32 mm的方形区域,计算该平面上的平均压强.由图2可以看出:当网格尺寸为1 mm时计算结果最高,网格尺寸小于3 mm时,挡板面上的静压变化不大;当网格尺寸大于3 mm时,挡板面上的压强变化很大;综合考虑计算精度和计算时间,选取网格尺寸3 mm对模型进行网格划分.

图2 网格无关性检验
1.3 方程求解与边界条件
采用标准k-ε湍流模型进行模拟,湍流模型中近壁面采用标准的壁面函数;标准k-ε模型的湍动能k和耗散率ε方程如下:
Gk+Gh-ρε-YM;
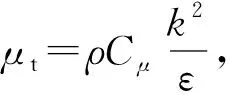
压力和速度的耦合采用Simple算法,压力的离散采用Standard形式,动量、湍动能、湍动能耗散率均采用Second Order Upwind形式离散.边界条件:进口边界条件为速度入口,出口边界条件为压力出口.固壁条件:固壁上满足无滑移条件及无剪切应力.模拟的工质为水,并假定流体不可压缩及物性参数为常数.
2 结果与分析
2.1 采用两种不同形状挡板情况下分离器内流体流动状态分析
对数十种组合条件下两种形状的挡板对分离器内部流场的影响情况进行分析,并选取了4种典型组合的流线云图,如图3~图6所示.
图3(a)为v=2 m/s,Ф=D=200 mm,H=400 mm条件下采用方形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图;图3(b)为该条件下采用球壳形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图.从图3可以看出:在大冲击间距和大挡板尺寸的情况下,方形挡板后部靠近上下两个壁面处出现了两个比较对称的较小涡流,主分离区内流体流动比较稳定,而球壳形挡板附近动能分布很不均匀,明显的上面偏大,因此主分离区上部出现了一个短路流,后部则出现了一个比较大的涡,虽然在此模型中采用球壳形挡板由于动能消耗较大,因此流场速度较小,但是从流体流动状态上看,采用方形挡板的流场分布更均匀,所以在此状态下方形挡板的稳流效果要比球壳形挡板好些.
图4(a)为v=2 m/s,Ф=D=200 mm,H=200 mm条件下采用方形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图;图4(b)为该条件下采用球壳形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图.此种状态为小冲击间距和大挡板尺寸,从图4可以看到,小冲击间距下流体冲击挡板后来不及形成涡就向挡板四周扩散,扩散过程中原始流体的动量传递给周围液体,自身的速度快速衰减掉,因此挡板前部的涡量很少,发展也不充分,缩小了冲击间距后,球壳形挡板后部的涡流不再明显,与图3(b)形成鲜明对比. 在此条件下x=500 mm截面的两幅图中可以看到,图4(a)中有两个明显涡流,而图4(b)中的流体流动状态比较平稳,可以说明在此条件下,球壳形挡板的稳流效果要比方形挡板好些.
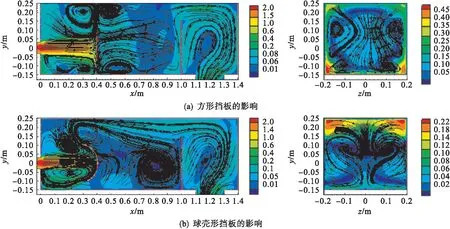
图3 v=2 m/s,Ф=D=200 mm,H=400 mm条件下分离器内部流场的流线云图
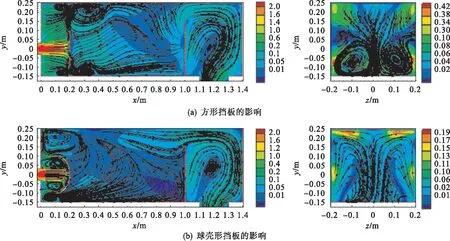
图4 v=2 m/s,Ф=D=200 mm,H=200 mm条件下分离器内部流场的流线云图
图5(a)为v=2 m/s,Ф=D=80 mm,H=400 mm条件下采用方形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图;图5(b)为该条件下采用球壳形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图.此种状态为大冲击间距和小挡板尺寸,与图3(a)、图3(b)相比较只有挡板的尺寸不同, 从图5可以看出:冲击距离的增大使得挡板前部的回流得以充分发展,形成反向涡的尺度呈增大趋势,挡板缩小以后,分离器内部流场明显紊乱许多,两幅图中显示的流场状态十分相似,可见在此状态下无论是采用方形板还是球壳形挡板,效果都差不多.
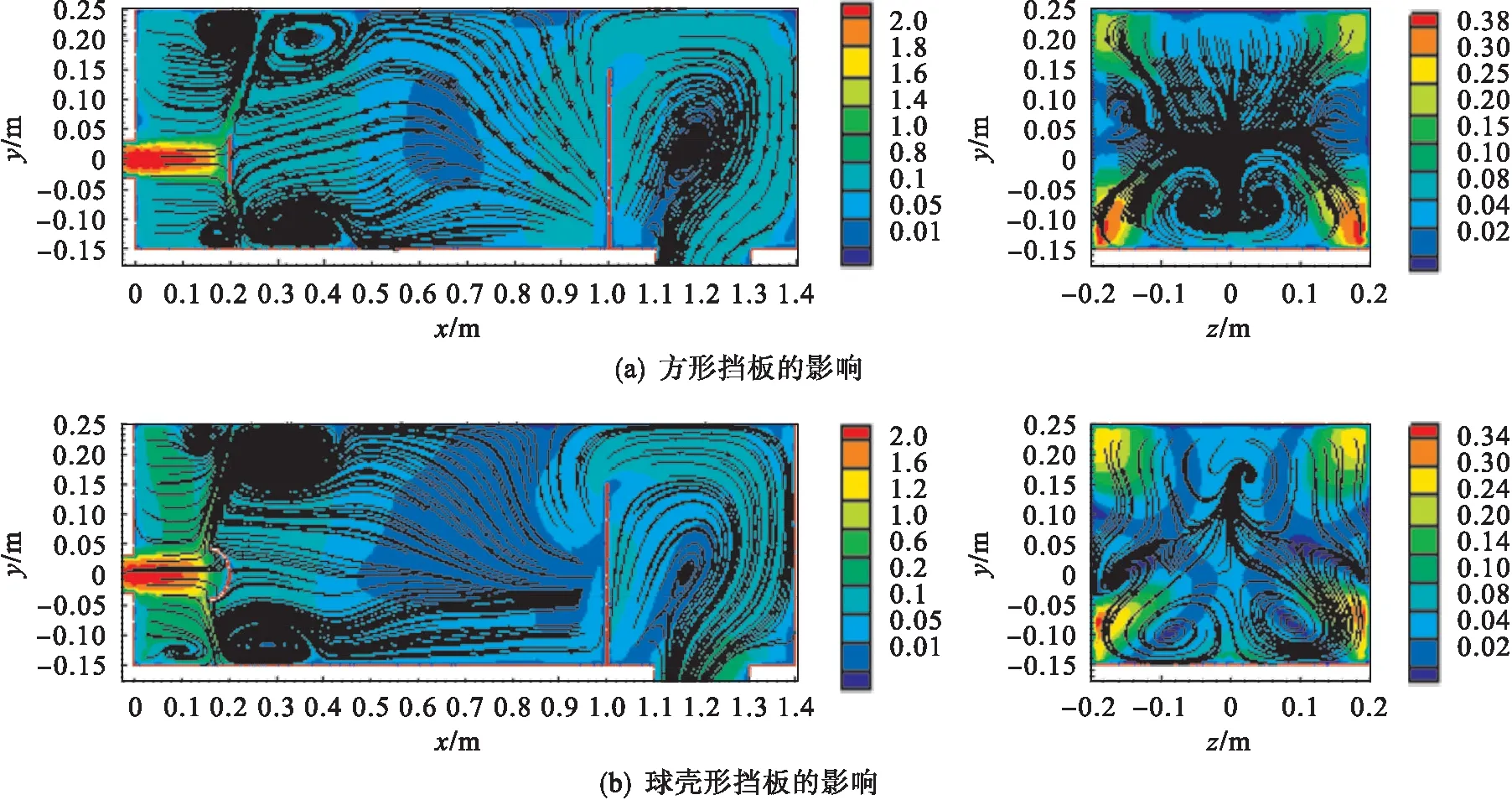
图6 v=2 m/s,Ф=D=80 mm,H=200 mm条件下分离器内部流场的流线云图
图6(a)为v=2 m/s,Ф=D=80 mm,H=200 mm条件下采用方形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图;图6(b)为该条件下采用球壳形挡板的分离器前中轴线纵向截面(左)和x=500 mm处截面(右)的流场流线云图.此种状态为小冲击间距和小挡板尺寸,与图5(a)、图5(b)相比较只有冲击间距不同,从图6可以看出:冲击间距缩小后,分离器内部流体流动的状态平稳许多,而且在此状态下无论是方形挡板还是球壳形挡板,对流场的稳定效果也是十分相似;但球壳形挡板较方形挡板的流体在横截面上的分布较不均匀,但分离区的流速相对小一些.
图3~图6挡板前的流场分布基本符合冲击射流特征.流体冲击流体到达防冲挡板附近时射流经历了显著的弯曲,存在很大的压力和速度梯度的.流体在冲击挡板前后形成不同大小和数量涡旋的环形回流区.环形回流区现象已由Fitzgerald[9]通过激光多普勒测速实验方法和焦磊[10]利用标准k-ε模型数值模拟方法验证.Sungsu Lee[11]在冲击射流中应用统计理论证实了普朗特湍流理论的施里赫延解,利用频闪观测法观测到了拟序结构的涡旋结构.无论是方形平面挡板还是球壳形挡板,在冲击间距较小时,挡板前部的环形回流区发展不充分,涡流尺度较小,而环形回流区后上方的顺时针涡流尺度较大,中轴线下方的逆时针涡流因受分离器底部的限制,涡流尺度较小[12];而且涡旋基本在中轴线上下对称分布.随着冲击间距H的增大,冲击射流两侧的环形回流区涡流尺度不断变大,中轴线上方环形回流区的中心向后上方移动,环形回流区的增大会卷吸周围更多的流体[13],使流场湍动范围增加,应当减小冲击间距来抑制回流区的发展.在分离区,方形板后的流场的流速比球壳形挡板的普遍要高,特别是在大的冲击间距的情况下,要大得多.
2.2 两种挡板对分离器内部流场影响的定量分析
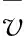
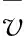
图7(c)、图7(d)中的模型采用了较大的挡板,可以看到在采用较大挡板的情况下,球壳形挡板的稳流效果明显比方形挡板好很多,而且入射速度越大,两者的差距越明显.这两幅图中均有“拐点”的出现,如图7(c)中球壳形挡板在v=2 m/s,H=300 mm比H=400 mm时的平均速度和平均湍流强度都要高,而图7(d)中还是球壳形挡板在v=2 m/s,H=300 mm时的平均速度和平均湍流强度却达到了最低,可见,对球壳形挡板做更为深入的单一性研究也是非常有必要的,因为随着条件的改变,会有“拐点”的出现,因此可以通过实验测量或数值模拟等方法确定出“拐点”,结合流动状态分析及速度、湍流强度衰减情况,最终确定出分离器防冲挡板的最佳尺寸S和冲击间距H,亦可在挡板后加装稳流构件等,进一步约束流体流动路径,降低流体速度和湍流强度,提高分离效率.
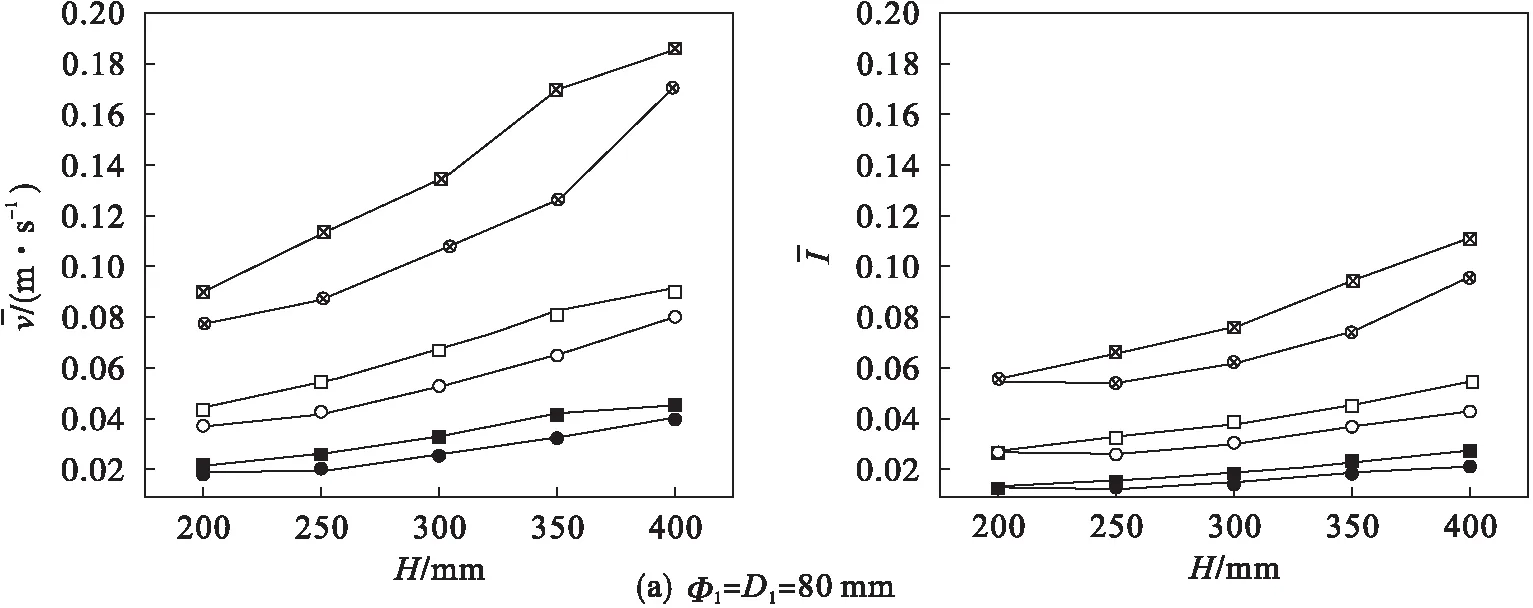
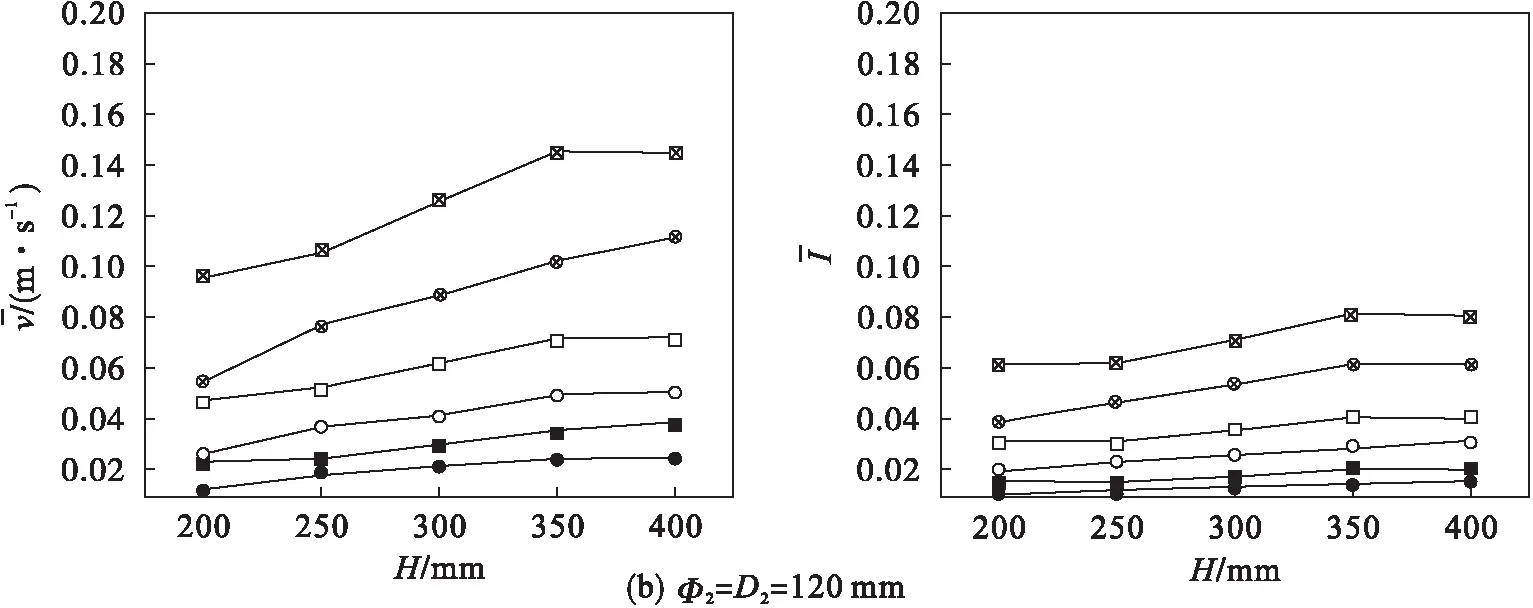
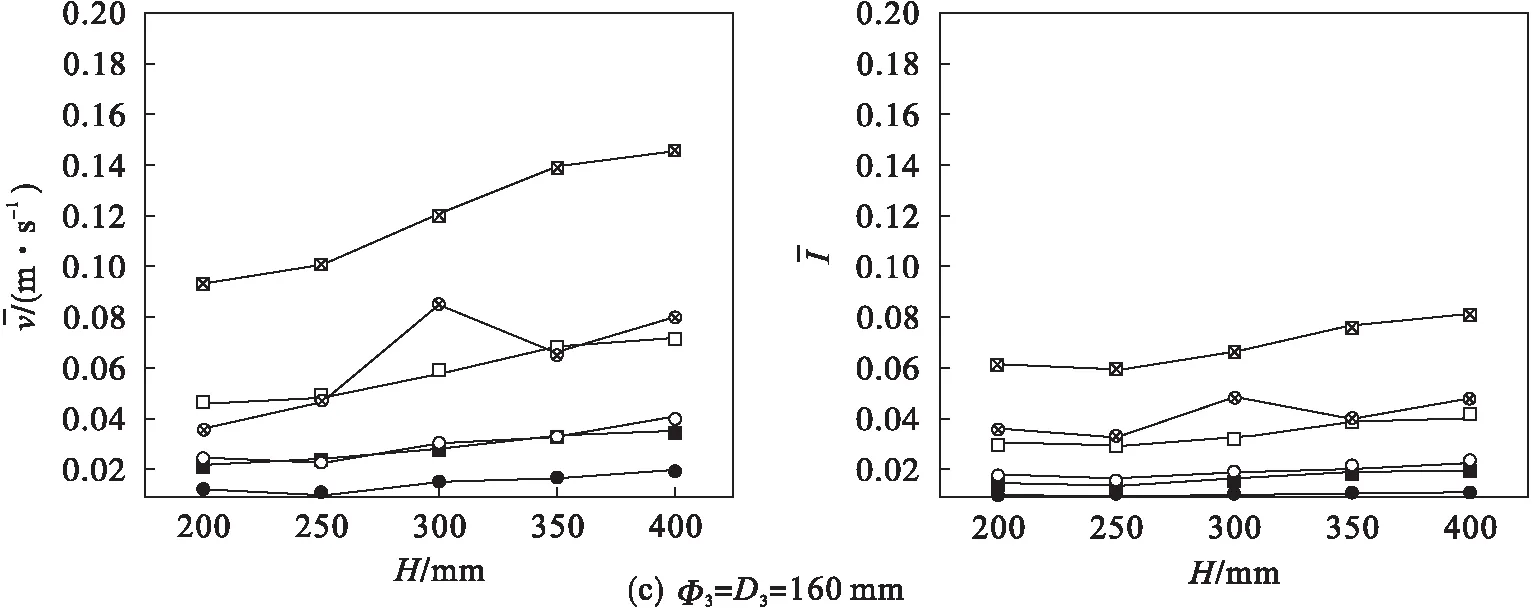
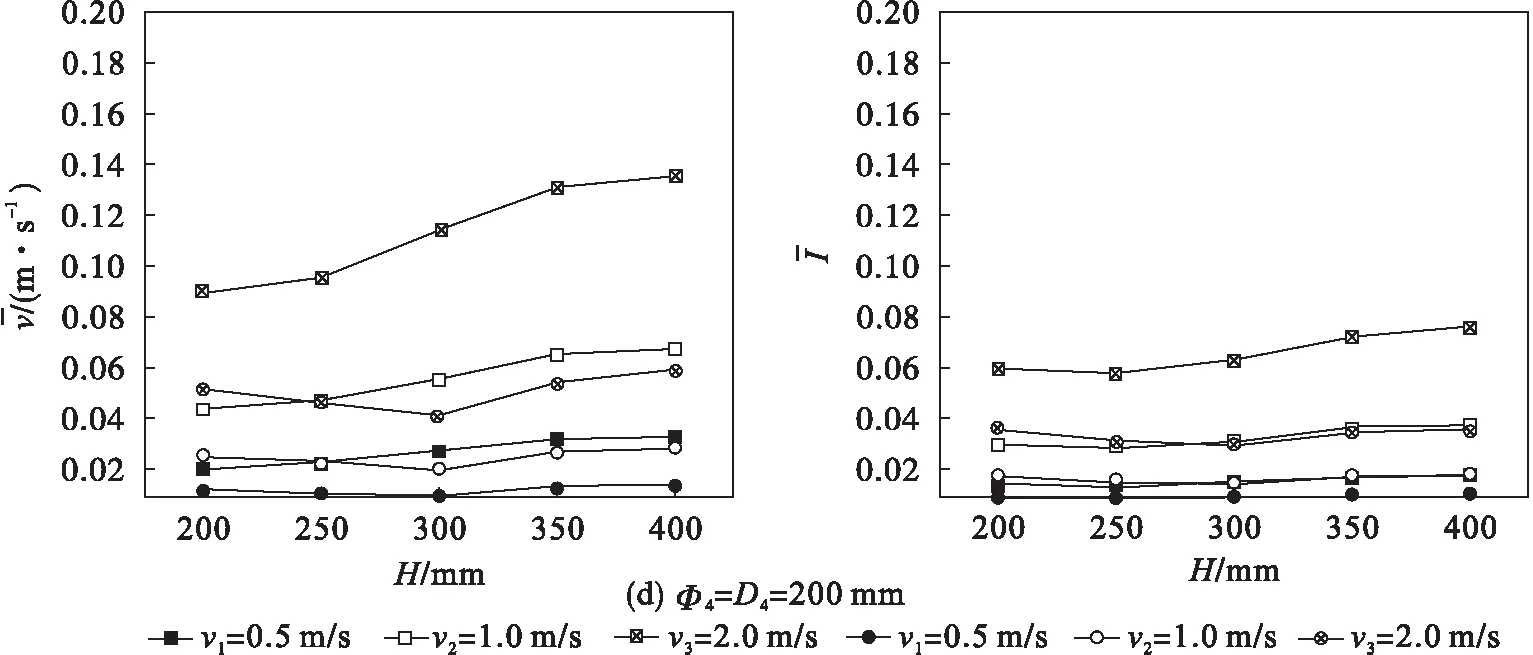
图7 两种防冲挡板在各种相同状态下横截面x=500 mm上的平均速度和平均湍流强度
3 结 论
(1) 在大冲击间距和大挡板尺寸的情况下,方形挡板后部靠近上下两个壁面处出现了两个较对称的小涡,而球壳形挡板区域由于动能分别很不均匀,后部主分离区处出现了一个比较大的涡,造成流体流动较不稳定,在此状态下方形挡板的稳流效果要比球壳形挡板要好.
(2) 缩小了冲击间距后,球壳形挡板后的涡流较小,稳流效果要比方形平板好些.大冲击间距和小挡板尺寸下,由于挡板和槽体的壁面效应减小,空间加大,涡得到充分发展,无论是采用方形板还是球壳形挡板,分离器内部流场明显紊乱许多.在大间距情况下,分离区的流速在球壳形挡板后要比方形板后大很多.
(3) 小冲击间距和小挡板尺寸情况下,由于涡的发展受到抑制,分离器内部流体流动的状态会平稳许多;由于挡板的形状影响较小,此状态下无论是方形板还是球壳形挡板,对流场的稳定效果也是十分相似,但球壳形挡板的流场分布较方形板的较均匀.
(4) 在以上所有相同状态下,采用球壳形挡板的模型都要比采用方形平板的模型拥有更小的平均速度和平均湍流强度,说明采用球壳形挡板,分离区的流速分布较均匀而且较平稳,应当尽量选用球壳形挡板进行工业生产.
