序列密码猜测确定攻击的现状研究*

李 枫，张文政，胡建勇，陈宇翔

（西南通信研究所，四川 成都 610000）

0 引 言

猜测确定攻击是密码算法分析中一种常用且有效的分析方法，目前主要应用于序列密码的分析。该方法最早出现在1998年的亚密会议上，由Knudsen[1]等人在分析RC4密码时提出。1999年，Bleichenbacher和Patel[2]使用猜测确定分析，发现了序列密码SOBER中的缺陷。2001年，Ekdahl和Johansson[3]在为NESSIE计划设计算法SNOW时，采用猜测确定攻击分析了算法的安全性。同年12月，Hawkes和Rose[4]提出了对于以字为单元的序列密码采取猜测确定攻击的一些思路。2006年，张斌和冯登国[5]采用猜测确定攻击对自收缩生成器进行分析，与其他分析方法相比，该方法达到了最佳时间复杂度和存储复杂度。2009年，Enes Pasalic提出针对过滤生成器的猜测确定攻击方法[6]。2012年，韦永壮等人对Pasalic的方法提出了改进和优化[7]。2010年，冯登国、冯秀涛等人用猜测确定分析实现了对SOSEMANUK[8]的猜测确定攻击和对于轻量级序列密码A2U2[9]的实时攻击。2011年，Abdelraheem等人[10]提出针对A2U2的猜测确定攻击。2015年，Yarom等人使用猜测确定攻击，对应用于RFID设备的序列密码Pandaka[11]进行已知明文分析,并提出了相应的应对举措。2017年7月，马振等人[12]针对Grain V1提出了一种与BSW采样技术结合的新型猜测确定攻击方法。

本文主要总结序列密码猜测确定攻击的研究现状及发展趋势，章节安排如下：第1部分概述猜测确定攻击；第2部分总结过滤生成器结构猜测确定攻击，并以A2U2算法的猜测确定攻击方法为例，说明组合器结构的猜测确定攻击过程；第3部分将总结多种方法融合的猜测确定攻击；第4部分对全文进行总结与展望。

1 猜测确定攻击概述

猜测确定攻击是已知明文攻击的一种。在已知明文攻击模型中，攻击者已知部分明文和这些明文对应的密文。相应的，攻击者可以恢复出将已知明文加密成相应密文的密钥，并将这些密钥应用于密码分析过程。

猜测确定攻击的基本思想是猜测序列密码的内部状态的一部分，再逐步利用已知密钥流比特确定其他的内部状态。该攻击是一种通用的方程求解方法，往往比单纯的枚举攻击要高效。对于序列密码而言，猜测确定攻击的目标是恢复某一时刻的所有内部状态或者种子密钥。一般步骤如图1所示。

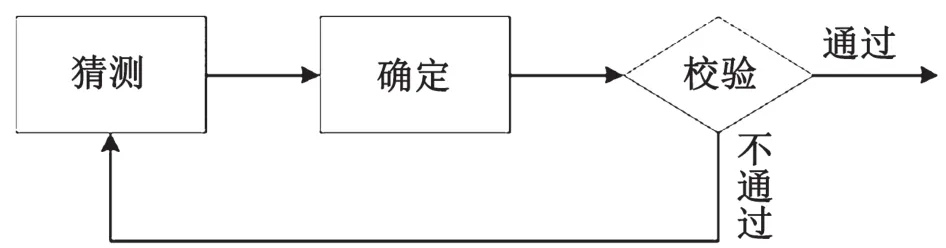
图1 猜测确定攻击流程

攻击者先猜测部分内部状态的值，然后根据截获的密钥值确定其他内部状态的值。使用确定的内部状态取值和猜测的内部状态取值生成相应的密钥流，然后和截获的密钥流进行对比。校验正确的通过，则完成攻击；不通过，则继续进行猜测确定的过程，直至找到正确的内部状态。

2 过滤生成器和组合器模型的猜测确定攻击

过滤生成器和组合器是序列密码两种应用广泛的结构，本部分总结针对这两种结构的猜测确定攻击方法。

2.1 过滤生成器结构的猜测确定攻击

过滤生成器结构是一种典型的以硬件为基础的序列密码结构，包含LFSR（Linear Filter Generator）和非线性函数F:GF(2)n→GF(2)m。猜测确定攻击不要求采集的密钥流的连续性。当分析的非线性过滤生成器具有较高的代数免疫度时，猜测确定攻击所需时间复杂度和数据复杂度低于代数攻击等传统分析方法。

2.1.1 过滤生成器猜测确定攻击

如图2所示，过滤生成器的一般情况表示为：

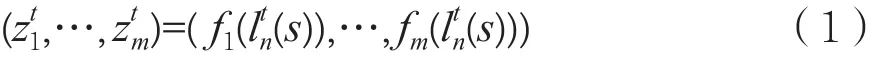
s=(s0,…,sL-1)为 t=0时 LFSR的 初 始 状 态，s,…,s)表示t时刻 LFSR 的n个状态，f,…,f0L-11m为布尔函数，,…,为对应密钥流比特。

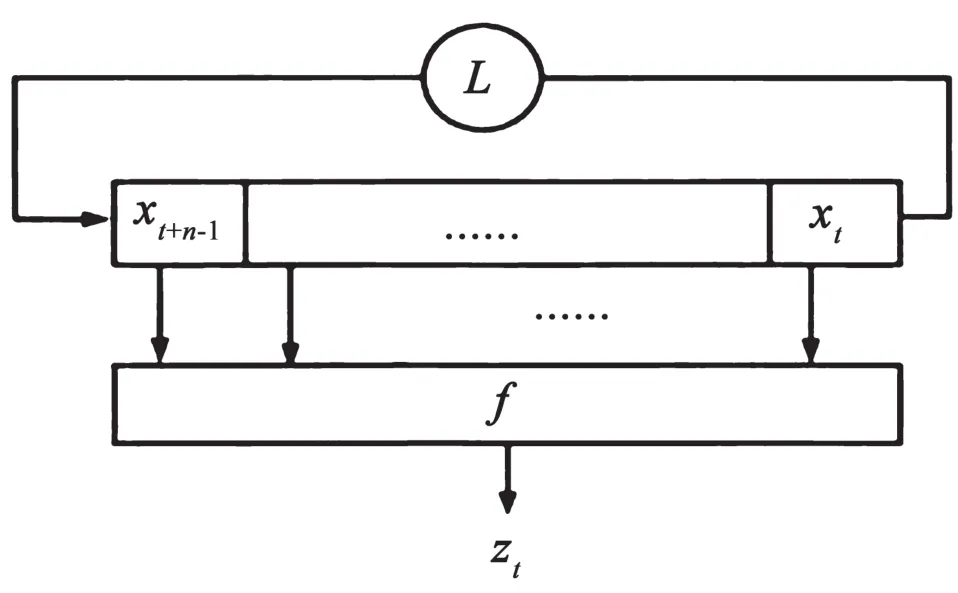
图2 过滤生成器

过滤生成器猜测确定攻击（Filter State Guessing Attack，FSGA）过程如下。

第一步：建立滤波器输入与输出对应关系的表格并存储；

第二步：每个观测到的zt=(,…,)对应2n-m个xt∈Szt，对于每一组xt=(,…,)∈Szt，建立方程联立求解。

对于每一组xt=(,…,)∈Szt，可获得n个关于s0,…,sL-1的线性方程，形如：

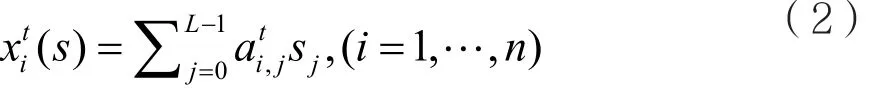
如果获得c个时刻的密钥，nc＞L，则很大概率每个有nc个方程的方程组是独立的，该方程组有唯一解或无解。该方法计算复杂度为2(n-m)cL3=2(n-m)(r+1)L3，其中，L=rn+v，0≤v≤n，L3为使用高斯消元法解有L元变量方程组的复杂度。预计算的时间复杂度为2n个操作，存储复杂度为n2n比特。

2.1.2 改进一：Generalized FSGA

过滤生成器的输入记为I0={i1,i2,…,in}，1≤i1≤i2≤…≤in≤L。n为输入个数，L为移位寄存器状态个数。采样时间设为t*1,…t*c，t*i=t*1+(i-1)δ，(1≤δ≤(in-i1))，

定义：

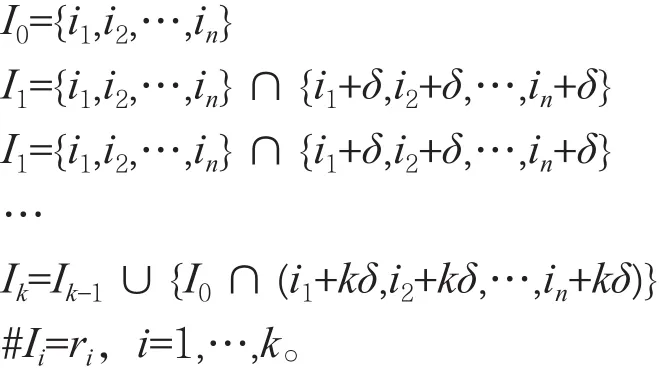
改进后的方法通过间隔采样，减少了采样结束后需要求解的线性方程组的个数，降低了计算复杂度。

它的计算复杂度为：

（1）当c≤k时，计算复杂度为：

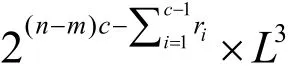
（2）当c＞k时，计算复杂度为：

预计算时间复杂度不变，仍然为2n个操作数，存储复杂度为n2n比特。

2.1.3 改进二：使用Maiorana-McFarland（MM）函数优化采样过程

向量MM布尔函数表示为F:GF(2)n→GF(2)m：

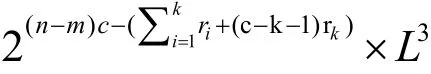
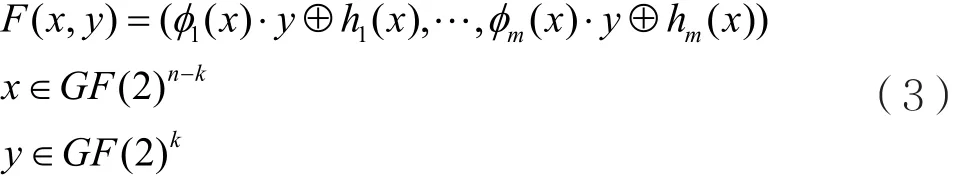
fi(x)是GF(2)n-k→GF(2)k的映射，hi(x)是任意GF(2)n-k上 布 尔 函 数，(i=1,…,m)当 n-k个 变 量x*∈GF(2)n-k固 定， f( x*, y) = φi(x*) · y ⊕ hi( x*)为k变量线性布尔函数。

把非线性过滤函数表示为：

fi(x, y)为MM函数。在ti时刻收集n-k个输入，可得到n-k个关于之前内部状态的线性方程。f1(x, y)，…， fm(x, y)是y∈GF(2)k上的线性方程。所以，猜测n-k比特输出，实际得到n-k+m＜n个关于内部状态的线性方程。

通过将过滤函数输入作为MM函数中的变元，该方法使用部分线性化，减少了采样过程所需要的采样次数和采样完成后需要求解的线性方程组的个数，降低了计算复杂度。改进后的时间复杂度TC为：

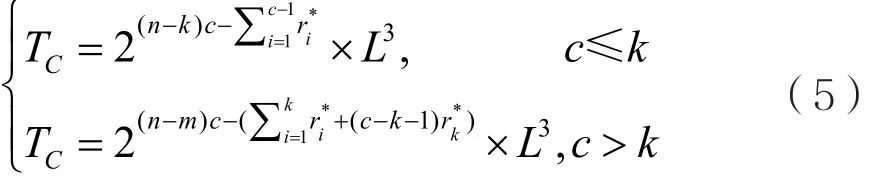
2.2 组合器结构的猜测确定攻击

组合器结构是一种典型的序列密码结构，广泛应用于以软件为基础的序列密码结构中。组合器结构的设计各异，因此目前针对组合器结构序列密码的猜测确定攻击多是建立在密码分析者的巧思之上，并没有形成固定的分析方法。

对于组合器结构的猜测确定攻击，密码分析者更多从猜测确定的本质——“分别征服”出发，基本思想为分析加密过程和内部状态之间的关系，如寄存器的递推关系、内部状态和密钥流之间的关系等，从而恢复所有内部状态。总体而言，对于组合器结构的序列密码，猜测确定攻击的思路如下：通过对非线性函数进行深入分析，找到函数设计中的弱点，通过猜测函数中的一些量，使其他状态可以由线性方程求得[12]；对于以字节或者字为单位的序列密码算法，可以通过分析算法在比特层面的关系式[8]，利用模加及LFSR等结构的研究，找到关于算法内部状态的方程，以降低计算复杂度。

下面以A2U2为例具体说明。

A2U2是应用于RFID等设备的轻量级密码算法，如图3所示。该算法在2011年由David等人提出[13]，密钥长度61 bit，包含7 bit LFSR、9 bit NFSR记为S17 bit NFSR记为L密钥编制和过滤函数。

图3 A2U2算法

LFSR更新：

ti+6,…,ti为i时刻LFSR的内部状态。

NFSR更新：

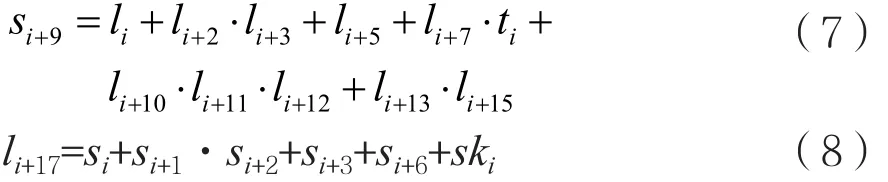
si+8,…,si为 i时刻S的内部状态，li+16,…,li为i时刻L的内部状态，ski是密钥编制生成的子密钥，为：

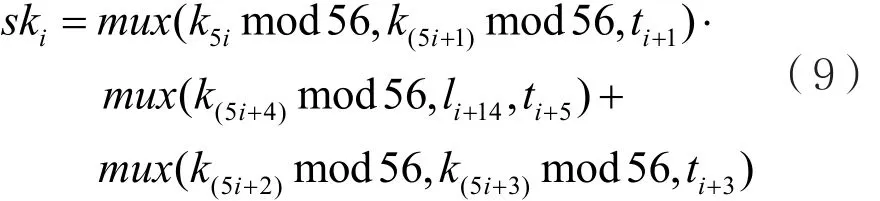
其中，三元函数mux(x,y,z)定义如下：

滤波函数：

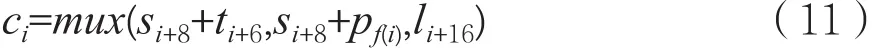
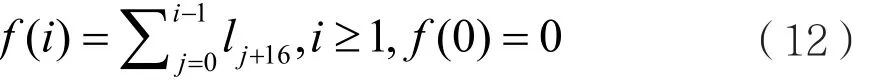
ci为i时刻的密文，pi为i时刻的明文。该攻击为已知明文攻击，具体步骤分为三个阶段。阶段1：猜测li(n≤i≤n+16)和f(n)，由关系式求 li(0≤i≤n)和 si(8 ≤i≤n+8)：

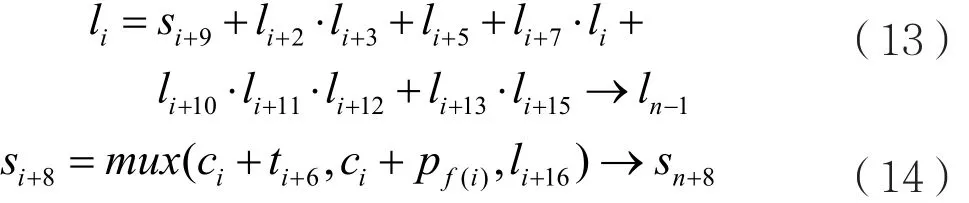
对于i=n-1,…,0，重复上述步骤恢复li(0≤i≤n)和 si(8 ≤i≤n+8)。

阶段2：恢复密钥ki(i=0,1,…,55)，根据密钥编制可以求得ski(i=8,9,…,n-1)：

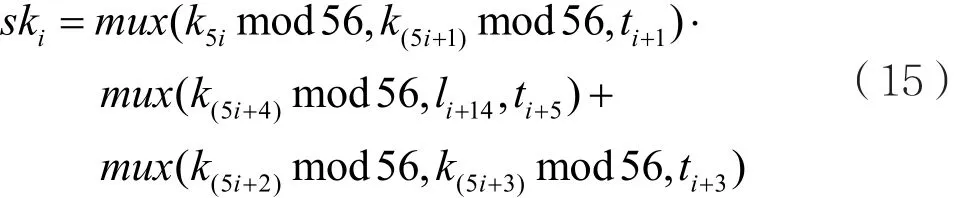
可以列出关于ki的n-8个方程。通过Q.Chai[14]的方法，当n≥512时，可以解出ki(i=0,1,…,55)；通过优化解方程过程[9]，n≥205即可恢复密钥ki(i=0,1,…,55)。

阶段3：通过Q.Chai[14]的方法，恢复密钥ki(i=56,…,60)，该过程的时间复杂度为25。

阶段1猜测ln+i(i=0,1,…,16)和f(n)(0≤f(n)≤n)，时间复杂度为O(217×(n+1))。

阶段2恢复密钥ki(i=0,1,…,55)，只有少量f(n)可以满足条件，时间复杂度为O(217×K×C)，K为满足条件的f(n)个数， K ≪n+1，C为求解密钥比特的复杂度。

阶段3复杂度25。

上述攻击过程所需总的时间复杂度为

O(217×(n+1)+217×K×C+25)。 该 方 法 选 择n=210，此时 217×K×C＜217×(n+1)，所以时间复杂度为 217×210 ≈ 224.7。

3 多种方法融合的猜测确定攻击

猜测确定攻击往往需要以某种手段获取密钥流生成器的某个中间内部状态。获取这种中间状态的手段多种多样，如相关攻击、时间空间数据折衷攻击、代数攻击以及错误攻击等方法。

3.1 猜测确定攻击与BSW采样

BSW采样是由A.Biryukov、A.Shamir和D.Wagner提出[15]的一种改进TMD攻击方法的技术。这种技术可以结合猜测确定攻击对序列密码进行TMD分析。

BSW采样的基本思想是：给定(F2)n上的函数(y1,y2)=f(x1,x2)，其中y1、x1为l比特，y2、x2为n-l比特。给定y1，如果对任意x2，都可以从f简单计算出一个x1，并进一步计算出y2。上述过程在限定y1的情况下，实际建立了从 x2到y2的映射f ´:(F2)n-l→ (F2)n-l。利用f ´建立目标状态空间的映射，此时状态空间缩小了2l。

BSW与猜测确定攻击的结合点在于，猜测确定攻击是攻击者先猜测或者用某种方法获取部分内部状态或者密钥流，获得的密钥流相当于BSW采样中的y1，猜测部分相当于x2，然后利用算法内部状态更新方程和所获得的密钥流推理出更多的其他记忆单元。这部分相当于固定y1，从x2经过简单计算求得x1，最后用所恢复得到的内部状态生成更多的密钥流与截获的密钥流进行对比，相当于通过x1、x2求得y2。因此，二者结合可以进行序列密码分析。

文献[12]采用该方法，使Grain v1的采样抵御降至2～29，与其他采样方法相比，达到了最佳效果。

3.2 猜测确定攻击与TMD（Time/Memory/Data）折衷攻击

时间/空间/数据（TMD）攻击[16]由穷搜索攻击和查表攻击两种方法混合而成，在选择明文攻击中以时间换取空间。它的时间复杂度比穷搜索攻击小，空间复杂度比查表攻击小。TMD攻击有两个主要的步骤。第一，预计算阶段。攻击者分析序列密码的结构，并把它总结到一张表中，表格中包括了密钥或内部状态，及与此对应的生成密钥流前缀，并对这些前缀按规则排序。第二，攻击阶段。攻击者观察密钥流，试图与表中的某个前缀匹配。如果匹配成功，从表格查询对应项，以此得到可能的内部状态或密钥。

在猜测确定攻击过程中，特别是对过滤生成器结构的序列密码，在猜测过程中常常需要进行预计算，通过建表将猜测值与原像空间的对应关系存储起来。表中包含了过滤生成器的输出和对应的可能的原像范围，然后在攻击阶段通过查表建立方程组求解。二者的结合很常见[6-7，12]。

3.3 猜测确定攻击与代数攻击

代数攻击的思想源于Shannon，认为一个密码算法可以表示为一个大的多变元多项式方程组，求解这个方程组就可得到密钥。代数攻击丰富了密码分析技术，不同于以往的基于统计的密码分析技术，而是依据密码内在的代数结构采用的新分析技术，通过建立初始密钥和输出密钥流比特之间的稀疏的超定代数方程组，运用线性化方法（包括Relinearization方法、xL方法、Gröbner基算法等）求解多元高次方程组以获得初始密钥。

猜测确定攻击的过程中，往往会产生庞大的线性方程组或者带有少量非线性结构的方程组。这时可以用Gröbner基等方法对方程组进行求解，或者利用Gröbner基确定出其他内部状态。二者的结合可以降低攻击复杂度[17]。

4 结 语

本文详述了针对轻量级序列密码算法A2U2的猜测确定攻击过程，总结了针对过滤生成器结构的序列密码的猜测确定攻击过程，概括了针对组合器结构序列密码的猜测确定攻击思路，以及BSW采样、TMD折衷攻击、代数攻击与猜测确定攻击相结合的方法。

随着序列密码猜测确定攻击相关技术的不断发展和完善，目前仍未解决的问题主要集中在三个方面：

（1）在GFSDA过程中，选择不同的采样点和不同的采样间隔，不同的采样点之间选取不同的采样间隔都可能导致不同的攻击复杂度。因此，算法设计中，如何选择最优抽头，使攻击复杂度最大，是目前猜测确定攻击方面的公开难题。

（2）Y. Wei提出了结合Maiorana-McFarland函数对过滤生成器的抽头进行部分线性化，以降低需要猜测的抽头个数，从而降低攻击复杂度[7]。是否有其他函数可以用于部分线性化，以减少攻击复杂度，可以作为进一步的研究方向。

（3）目前，对于组合器结构的序列密码的猜测确定攻击大多依靠密码攻击者的一些巧思，没有统一的算法和标准。密码算法是否能抵抗猜测确定攻击，只能由现有的攻击方法进行检验。因此，相关抗猜测确定攻击的布尔函数指标的提出十分必要。