变频多通道通带相位一致性控制研究*

王晓光

（中国电子科技集团公司第十研究所，四川 成都 610036）

0 引 言

多通道接收机在阵列天线、调零天线、T/R组件等电子设备中得到了广泛应用[1]。理论上，多通道要求能够做到通道间电性能互易，因此多通道的电性能一致性是设计实现的关键[2-5]。接收机中与通道相关的典型指标包括功耗、线性度、幅频响应、相位响应和通道互耦等[6-8]。其中，包括功耗、线性度、幅度等多数指标通过前期设计可以得到较好的保证，实现过程中调整偏差也较为方便。通道互耦很大程度上依赖于硬件的前期设计，也可以通过仿真进行前期验证；而相位一致性则对实现过程敏感。由于通道内器件的差异性、布局布线的差异性以及级与级之间匹配的差异性，各通道间的相位差别会显著比设计值偏大，而相位上的差别直接导致了群时延的不一致。因此，有必要从理论上分析各级对通道总时延产生的影响和产生这种差异性的原因，从设计上对接收机通道电路的时延一致性进行控制。

1 变频通道理论模型

1.1 变频通道原理

一个典型的下变频通道，包含了放大、射频滤波、混频以及中频滤波等单元电路，原理如图1所示。

图1中，级联各级电路的传输函数都包含了对幅度和相位的响应，理论上都可能贡献相位差。根据下变频通道中信号的流程，以下将逐级分析产生群时延差异的原因。由于群时延和相位满足：

图1 变频通道原理

即时延是相位的一阶导数。中心频率附近的窄带内线性的相位对应相同的群时延，通带内不同频点之间的相同的线性相位增量对应相同的群时延增量。为此，本文将从相位角度进行量化分析。群时延和群时延波动分别对应中心频点的相位一致性和通带内相位波动的一致性。

1.2 放大器相位响应分析

放大器是是二端口有源器件，当工作在小信号时，其S参数矩阵为[9]：

由式（2）描述的转移函数对相位的一阶导数为常数，即时延近似为常数。以上的分析假定了输出信号也为小信号，不至于引起器件不可忽略的非线性的情形。当对通信系统相位特性要求很高时，还需要考虑器件的非线性效应引起的相位调制，即放大器增益压缩对相位的影响。

放大器单音输入考虑非线性的输入输出关系的数学表达式为[10]：

输入信号记为：

其中ω为角频率，φ0为初始相位。

考虑实际失真不严重的情形。输出信号中，以直流分量及三阶以下奇偶次谐波的输出作为近似：

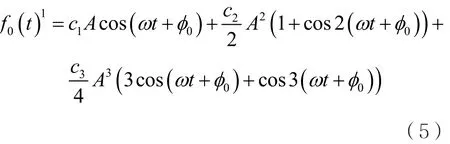
通过后级滤波器取出的频率分量为：

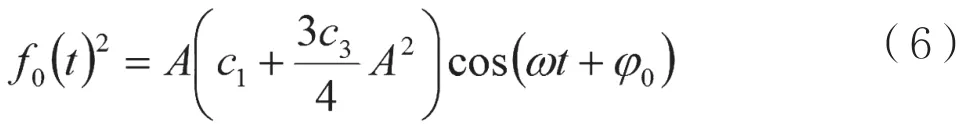
输入信号的幅度不是绝对的恒定，由此线性及三阶项遵循矢量合成。

假定：

考虑了放大器单音输入的非线性效应后，高阶产物与基频合成矢量的幅度矢量叠加。可以看出，输出信号同时受到了幅度和相位两种调制[11]，使得输出相对输入产生了相移。作为具有一定带宽的带限信号，取带宽中心频点ω0及BW3dB定义的两个频率上下界(ωd,ωu)，记输入信号为：

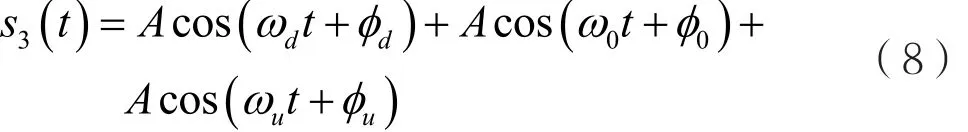
根据式（3），输出信号为：

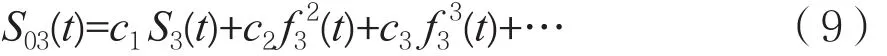
考虑线性项和三阶项，互调分量在带外可以被后级滤波器滤除暂不予考虑。

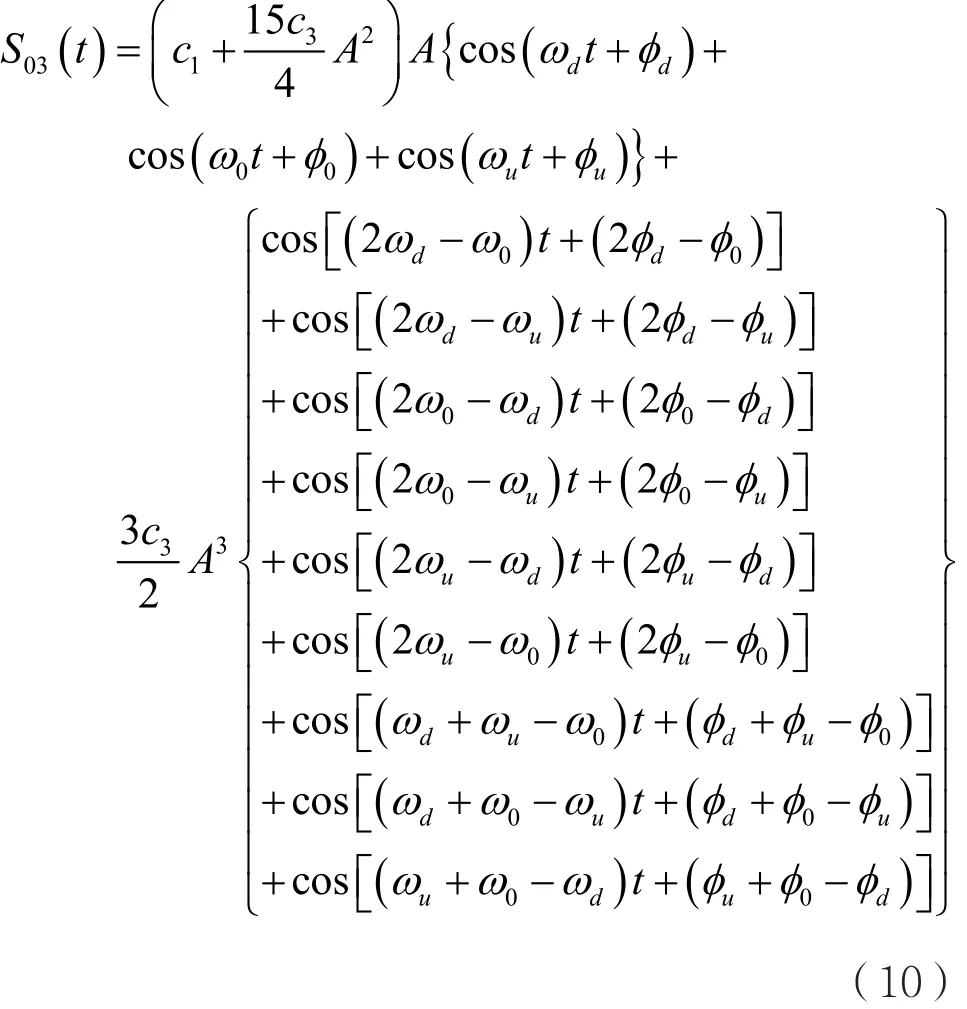
式（10）需满足：

放大器在此前提下可以看作线性器件，此时的交调产物对基频的影响可以忽略不计。因此，通道的相位保真需要放大器工作区的线性度尽量高，以减小幅相调制。由于不同放大器高阶产物的差异性，选择放大器的重要参数是1 dB压缩点而不是IIP3，以及合理的设计裕度，保证最大输入信号时放大器的输出仍离1 dB压缩点有一定的功率回退。

2 混频器的相位响应分析

下变频混频器本质上是用器件的非线性将功率较强的LO本振信号和RF输入信号同时输入三端口器件，然后利用LO对非线性器件的开关作用产生新的频率分量。由LO对非线性器件形成的开关效应，中频输出电流为[12]：

令输入射频信号为：

LO的初始相位由于锁相环初次锁定时的随机相差φLO，每次都会存在一定差异，记LO信号为：

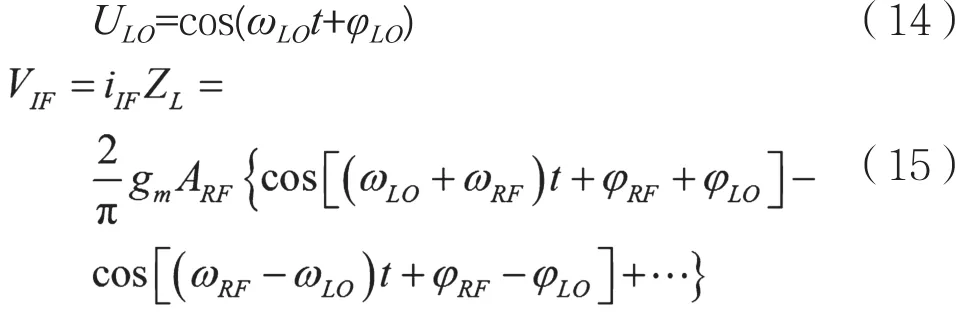
下变频的中频输出是由带通滤波器取出的差频分量，即：

多通道中每个通道本振同源，记本振到各个通道的电长度在相位上的尺度分别为：

对应的每个通道混频器的输出为：

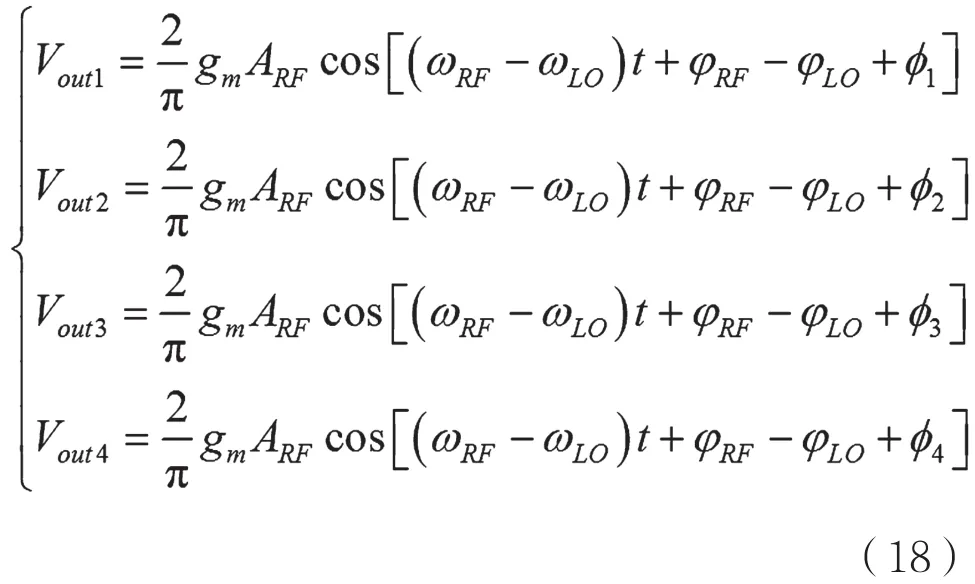
假定空间信号满足远场近似条件，天线具有理想的相位中心。通道的中心相位一致性取决于混频器输出的中心相位一致性，而该指标通过本振输出到各通道的电长度一致性来保证。混频器相对于工作带宽为宽带器件，理想情况下在通带内相位随频率线性变化，其波动取决于与前级放大器的匹配程度。

而实际的混频器工作时的匹配需要考虑分布参数的影响和硬件实现的不理想情况。以对消奇数阶谐波的平衡混频器为例，需要考虑由外围电路的差异性导致的混频器输出相位误差，平衡式混频器内部两路输出分别记为V1、V2，理论上相位差为π，考虑实际因素的矢量合成，如图2所示。

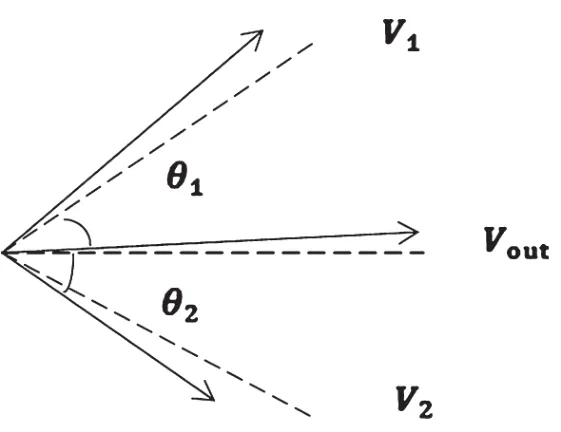
图2 混频器的AM-PM

其中：

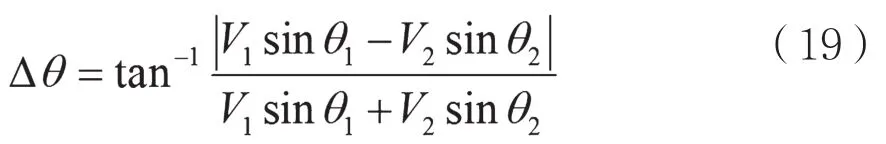
幅度的不平衡引起了相位上的误差，一致性要求各通道混频器的外围器件电性能要尽可能一致，以减轻电性能参数的差别，形成幅度对相位的调制而引起的通道间相位差异。

如前所述，混频之前的本振输入信号到达各个通道的电长度，其目标是完全一致。受限于具体实现，首先应设计成电长度相差小于本振波长λLO，无跳周期的基本一致，然后由移相网络完成一个周期内的相位搬移。

下变频通道满足如下关系：

混频器中输入本振端相对输出中频波长较短，只需要走较短的电长度就可以对相位进行较多的搬移。在不同的通道混频器本振的输入端设计不同的移相参数，可以对到达相位进行调整，使通道间的中心相位差基本一致。

本振移相电路可以选择分布参数或者集中参数的形式，本质上是改变LO微波信号路径的长度来改变各通道LO的电长度，进而调整各通道混频器中频输出的中心频点相位一致性。集中参数中的电感和电容有移相功能，电容的端电压落后于电流，电感的端电压超前于电流，由此组合出来的低通或者高通滤波器原型，可以实现(0,π)之间的相移调整。

图3为两种移相网络原型滤波器拓扑结构，可以单独或者组合使用。它的传输函数的设计原则是幅度几乎无衰减地同时有较大相移。由于不同的本振功率可能对混频器的中频产物产生一致性影响，移相网络应在ωLO处有几乎一致的差损。移相网络本身也是谐振网络，可以同时抑制本振带外的杂散分量。需说明，仿真同时关注幅度衰减和相位两个指标。

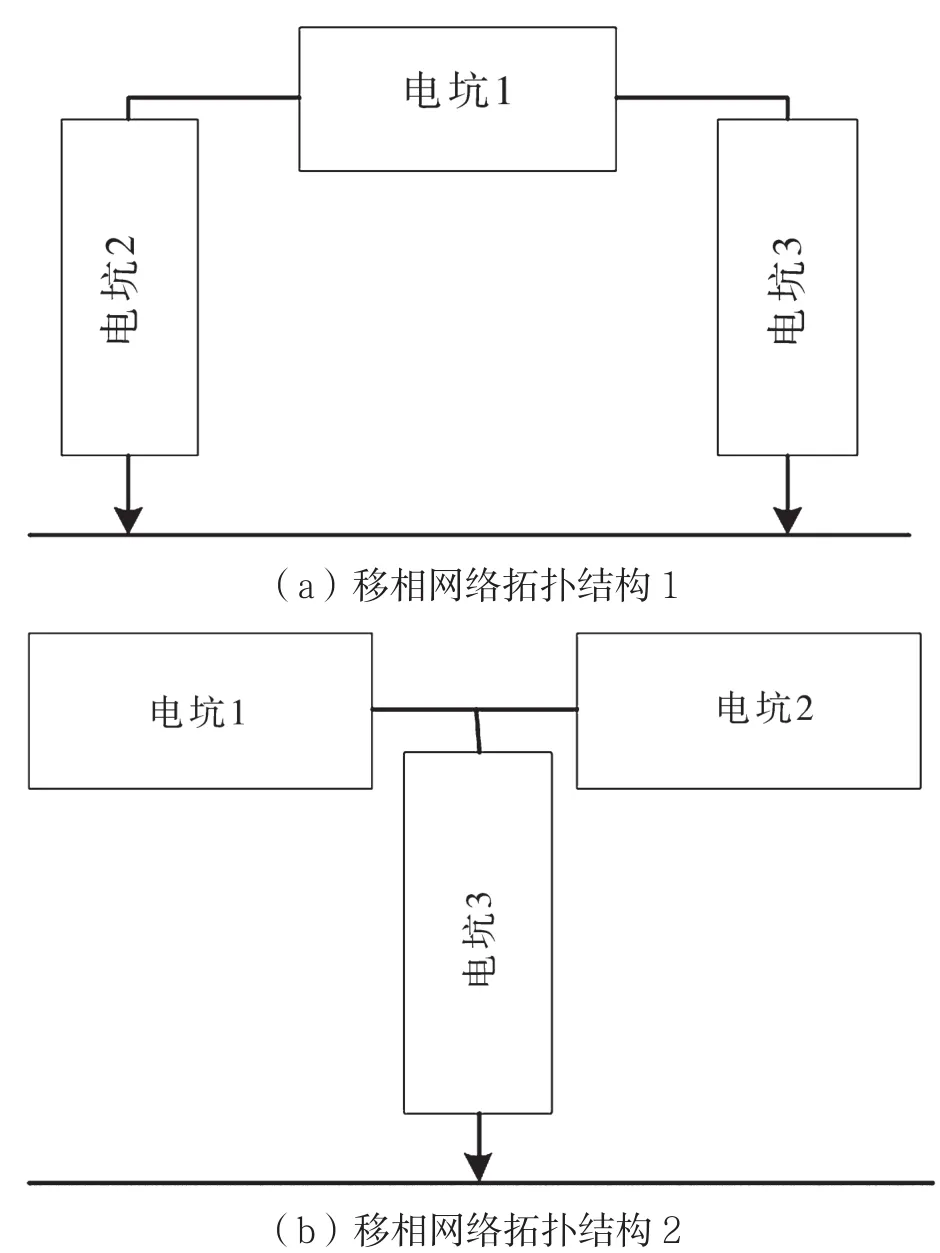
图3 移相网络拓扑结构

通过仿真可以看出，图4、图5两种基本移相网络可以灵活实现相位超前或者滞后，根据实际测量到的通道本振的相位，选择某个通道作为主通道，在此基础上测量其他通道的相对相位关系，将相对超前的通道经过相位滞后，将滞后的通道相位超前，最后所有的通道的相位调整到同一个起点上，达到中频中心相位的一致。

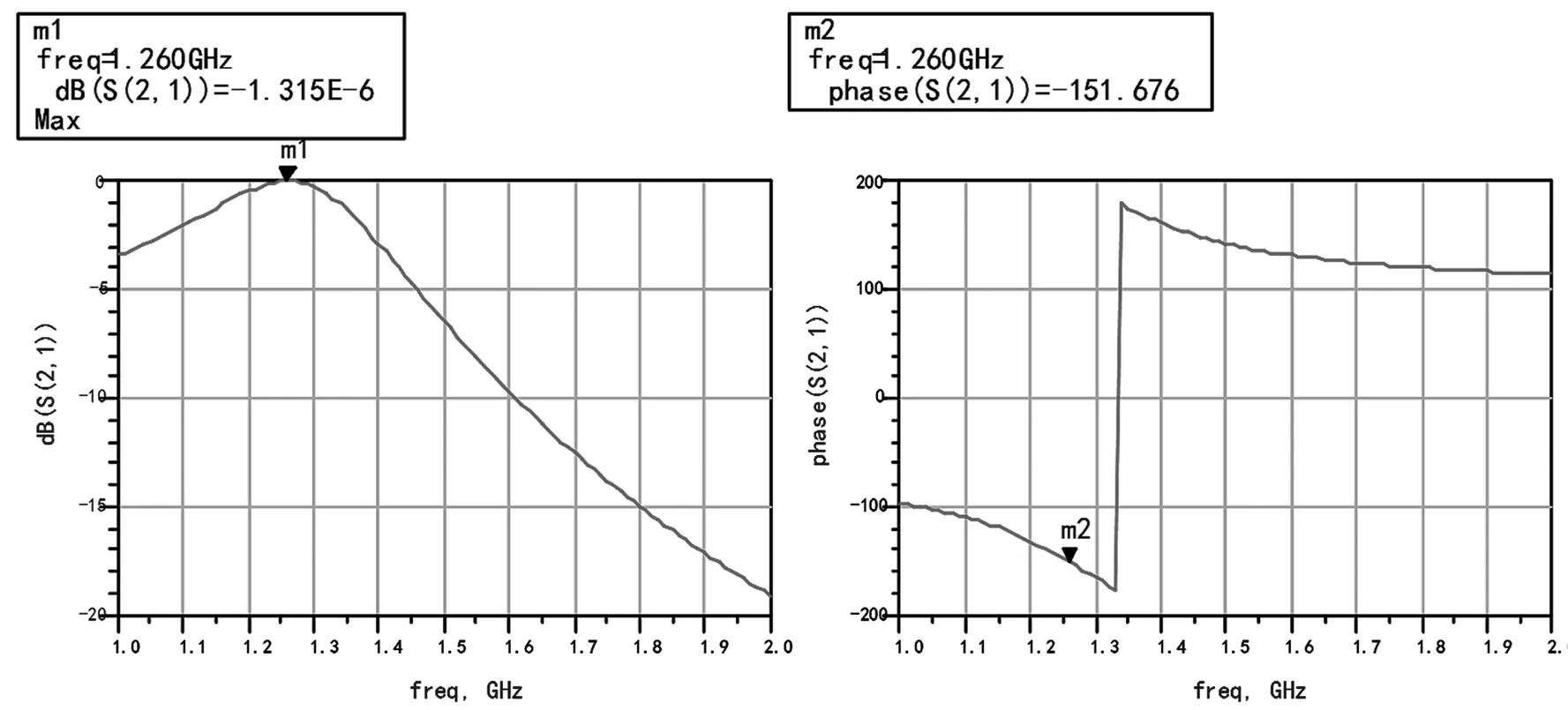
图4 低通移相网络仿真

图5 高通移相网络仿真

以四通道为例，选择第一个通道为参考通道，相位的相对关系有三个，分别是(ch1-ch2)、(ch1-ch3)和(ch1-ch4)。调整前，三个通道的相差都比较显著，如图6所示。

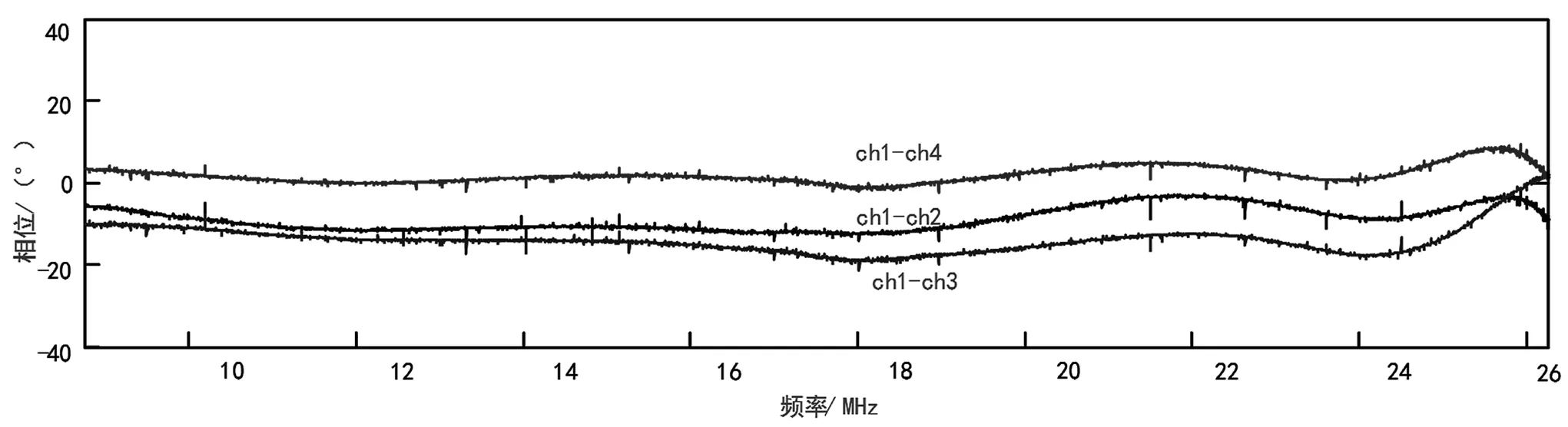
图6 通道间的相位响应

通过选择合适的移相网络和电参数，将其中一个通道的LO相位调整，使得(ch1-ch2)、(ch1-ch3)尽量接近。按照这个方法再调整(ch1-ch4)，结果如图7所示。这样经过两次调整后，中心相位的一致性可以得到较好的保证。

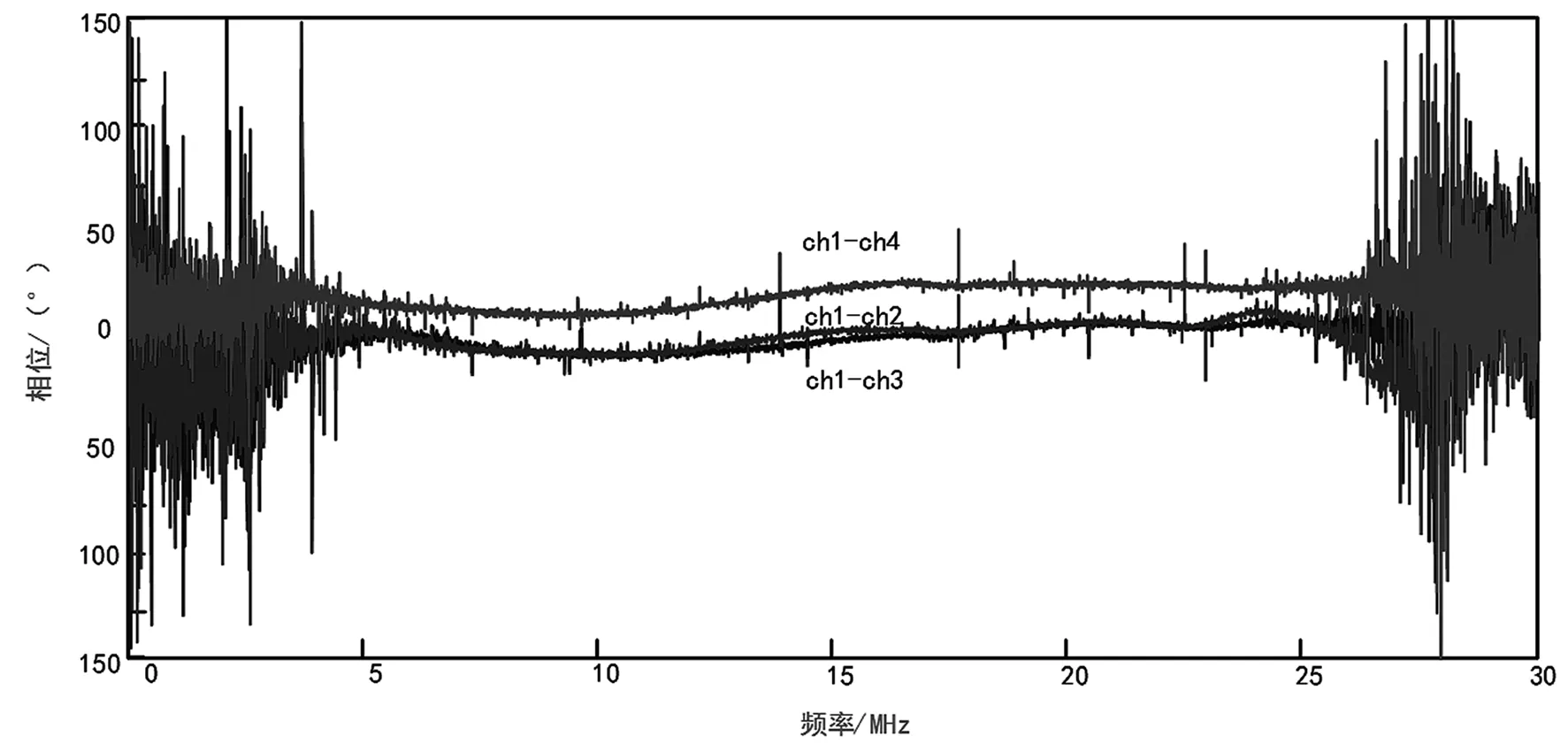
图7 通道2校正后的相位响应

3 中频滤波器的时延分析

通常意义上，中频滤波器是带通滤波器，其传输函数是低通与高通滤波器的组合函数。因此，中频滤波器的带内波动和带外抑制指标之间的关系更复杂。无论对应的原型滤波器是最大平滑二项式滤波器还是等波纹滤波器，它的通带内都不可避免会有幅度和相位波动。通带内的相位波动通过设计中频的移相网络进行调谐。

对应多通道接收设备，有对应的一组中频滤波器，控制多通道间相位的一致性。它的主要工作是设计一种滤波器，通过仿真选择一种合适的电路拓扑形式，从设计形式上保证其带内相位参数对滤波器的离散型尽量不敏感。更重要的是，由于仿真并不能做到精确求解，还需要进一步通过设计调试，按照通道数目将相位一致性匹配分组使用。

对于相位一致性要求很高的场合，对通带内的相位波动，应通过调整中频滤波器来改变通带内的相位响应曲线，使通道间的通带相位一致。同时，结合在混频器的本振输入端调整中心相位，将全通带的相位一致性调整到最接近的状态。

在分析产生通道相位差的机理基础上，通过建立放大、射频滤波、混频的相位失真数学模型，分析中频滤波等单元电路，形成的通道原理如图8所示。图9、图10则分别为调整后的通带相位一致性和通带一致性。

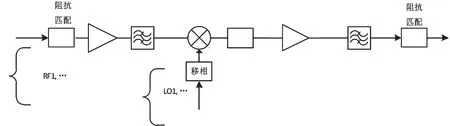
图8 改进的幅相一致性通道原理

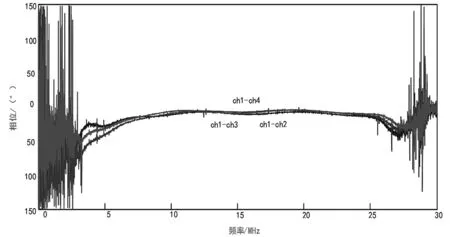
图9 调整后的通带相位一致性

图10 调整后的通带一致性

4 结 语

本文分析了各级电路的相位差异产生机理，根据群时延与相位的微分关系，群时延一致性通过相位一致性来保证。相位不一致产生的原因主要包括本振电长度的差异，各级电路的离散型以及级联各级之间不完全匹配形成驻波，影响幅度和相位。因此，相位一致性的调整需要从本振和通道二方面考虑。级联的响应不是各级级联的线性函数时，级联的相位效果会进一步恶化。因此，级联实现的关键是做好本振流程和信号流程上各级端口的匹配，尽量减小幅度和相位的失真。

通过分析下变频接收机的各个级联电路，剖析可能引起相位不一致的原因和各级相位不一致的机理，针对放大器和混频器的AM-PM效应，提出了改善线性度，进行功率回退使用，从设计上保证余量，改善相位失真；对于混频器，分析本振相位不一致的原因和采用的调整方法；对于中频滤波器，分析了设计原则和实现原则。相位一致性的保证，是从原理设计到硬件实现的全过程控制。从本文的讨论可以看出，各级电路之间的驻波是重要的关注指标。驻波较差时，由于反射较为严重，会引起AM-PM效应，使得最终的设计效果与理论分析相差较远，相位的一致性也会受到影响。