光子计数无线光通信系统信噪比分析*
2018-10-15印蕾
印 蕾
(江苏省军区数据信息室,江苏 南京 210009)
0 引 言
随着无线光通信的不断发展,人们对通信距离的要求不断提高,促使对接收端探测器的灵敏度提出了更高要求。近年来,光电探测器不断发展,出现了具备单光子灵敏度的探测器。其中,盖革模式雪崩光电二极管(GM-APD)由于在近红外波段的良好性能[1],被广泛应用于深空光通信[2]、水下光通信[3-4]、量子密钥分发[5]和自由空间光通信[6]。近10年来,在NASA的深空探测项目中,美国麻省理工林肯实验室与加州理工喷气推进实验室,一直致力于基于GM-APD阵列地面接收终端的设计与论证[7-8],计划实现地球—火星、地球—月球的全天候高速率通信。
2014年,Danial Chitnis、Steve Collins基于泊松分布模型建立了基于GM-APD探测器阵列的误码率模型,并实验验证了基于GM-APD探测器阵列通信系统的误码性能[9]。但是,目前对基于光子计数的通信系统信噪比分析还很匮乏,而现有的半导体雪崩探测器信噪比公式并不适用于GM-APD,因为它针对的对象是工作在线性模式的APD[10]。传统的APD信噪比公式通常以电流为变量,而GMAPD工作于光子计数模式下,信号强弱由雪崩脉冲的计数值来衡量。所以,现有的APD信噪比表示方法显然不适用于GM-APD。本文主要基于工作于门控模式下GM-APD的触发模型,并根据光子计数过程推导出GM-APD阵列的信噪比公式,然后对其进行数值仿真与理论分析。
1 GM-APD工作模式
GM-APD是在APD两端加上大于雪崩电压的反向偏压。此时,它的增益系数趋于无穷大,只要内部产生一个光生载流子就会触发雪崩效应,产生能被外部电路检测到的雪崩电流。但是,雪崩若不加以抑制会一直进行,直至击穿探测器。所以,需要雪崩抑制电路,使APD发生雪崩事件后及时降低偏压抑制雪崩效应;且在间隔一段时间后重新加上反向偏压,使探测器处于工作状态。GM-APD被外部电路淬灭到其重新处于工作状态的时间间隔,称为探测器的死时间[11]。在死时间内,探测器无法响应任何光子。
实际应用中有三种抑制雪崩的方式:被动抑制电路、主动抑制电路和门控电路。其中,工作于门控模式下的GM-APD具有较短的死时间、较低的暗计数率和后脉冲率,所以一般采用门控模式。如图1所示,GM-APD工作在门控模式下,在外部输入的触发信号控制下,在内部产生了一个宽度可调的门控信号,使APD在短暂的门控时间内处于盖革模式,以探测可能会在该时段内到达的光子。如果一个门内检测到雪崩信号,则会在输出端产生一个雪崩脉冲输出,并在此后的死时间内不再产生内部的门控信号。GM-APD是一种间隔工作的探测器,可基于其以上特点推导适用于光子计数通信系统的信噪比公式。

图1 GM-APD门控模式下的工作时序图
2 信噪比模型
由于探测器产生光电子过程服从泊松分布[12],所以t1~t2之间产生k个光电子的概率为:

式中K(t1~t2)代表t1~t2探测器产生的平均初始光电子数。初始光电子有三种来源:信号光子、背景光子和内部暗计数[13]。定义单个门内信号光子数为λs、背景光子数为λb、暗计数为λd、探测器量子效率为η,可得单个门内总平均光电子数为:

定义探测器阵列由m个GM-APD组成,并将接收到的光子平均分配到阵列中每个GM-APD,可得GM-APD单个门内总平均光电子数为:

假设每个门内探测器内部只要产生至少一个光电子就会产生雪崩脉冲,并最终产生一个计数值。所以,由式(1)和式(3)可得GM-APD单个门内无雪崩脉冲产生的概率为:

相反地,单个门内有雪崩脉冲产生的概率为:

由式(5)可得,由探测器实际计数值表示单个门内信号光子数的估计值为:


n1为输出为1的门个数,nm为门的总个数。由于n1服从二项分布,可得的均值与方差分别为:


对式(10)求期望,可得:


由式(12),可得:

结合式(10),并略去式(12)大于2次方的项,可得:


由于:

结合式(13)、式(14)和式(15),并略去大于2次方的项,可得:

由式(6),可得:

将式(9)、式(17)带入式(16),可得:

单个信号周期内总信号光子数为nλs,可得信噪比表达式为:

3 仿真分析
根据推导的信噪比式(19),仿真分析单个门内信号光子数、信号周期内开门次数n、阵列中GM-APD个数m对信噪比影响。计算过程中,取探测器量子效率为10%。
图2为单个门内背景光子数λs不同情况下,信噪比随单个门内信号光子数λs的变化曲线。计算过程中,单个门内暗计数λd=8×10-6,图2(a)、图2(b)、图2(c)三个子图分别对信号周期内开门次数n、阵列中GM-APD个数m取不同值的情形。图2表明,信噪比随信号光子数λs的增大而增大,且当λs≥2时逐渐趋于平稳。该系统噪声主要来源于GM-APD阴极产生信号光电子、背景光电子与内部暗计数的泊松过程再累加进计数中的二项过程。当信号光子数λs较小时,背景光子和暗计数为主要噪声来源,此时增大λs,信号迅速增大,而主要噪声无变化,所以λs≤2时信噪比增加速度较快。反之,当λs较大时,信号光子为主要噪声来源,此时增大λs,信号随噪声一起增大,所以λs≥2时信噪比逐渐趋于平缓。

图2 单个门内背景光子数不同情况下,信噪比随单个门内信号光子数的变化
对比图2的三个子图,当信号周期内开门次数n、阵列中GM-APD个数m变化时,信噪比变化的整体趋势基本不变,即λs≤2时信噪比增加速度较快。
由信号光功率计算公式:

当信号光波长λ=1550 nm、探测器门控时间tw=5 ns、触发时钟周期T=50 ns,可得单个门内信号光子数为2个时,信号光峰值功率为-72.9 dBm。当接收端信号光峰值功率达到-72.9 dBm后,通过增加信号发送功率来提高信噪比效率将会非常低,应考虑通过其他方式来提高系统信噪比。
图3为单个门内暗计数λa不同情况下,信噪比随探测器阵列GM-APD个数m的变化曲线。计算过程中,信号周期内门次数n=10、单个门内信号光子数λs=10、单个门内背景光子数λb=1。图3表明,当探测器阵列较小时,信噪比随阵列中GM-APD个数m增大而增大(m≤15);而当探测器阵列较大时,信噪比随阵列中GM-APD个数m增大而减小(m≥15)。因为GM-APD存在暗计数,随着m的增大,由暗计数产生的噪声一直在累积。相比之下,信号光子与背景光子产生的噪声变化程度较小。所以,当m≥15时,信噪比随m增大而恶化。由图3可得,暗计数λa越大,信噪比开始下降点m越小。此外,当在GM-APD暗计数大于8×10-4个/门、阵列增大到下降点时,信噪比反而会下降。于是可知,根据GM-APD暗计数大小选取合适的探测器个数m,能极大地改善系统信噪比。如果盲目增大阵列规模,则会导致系统信噪比的急剧恶化。
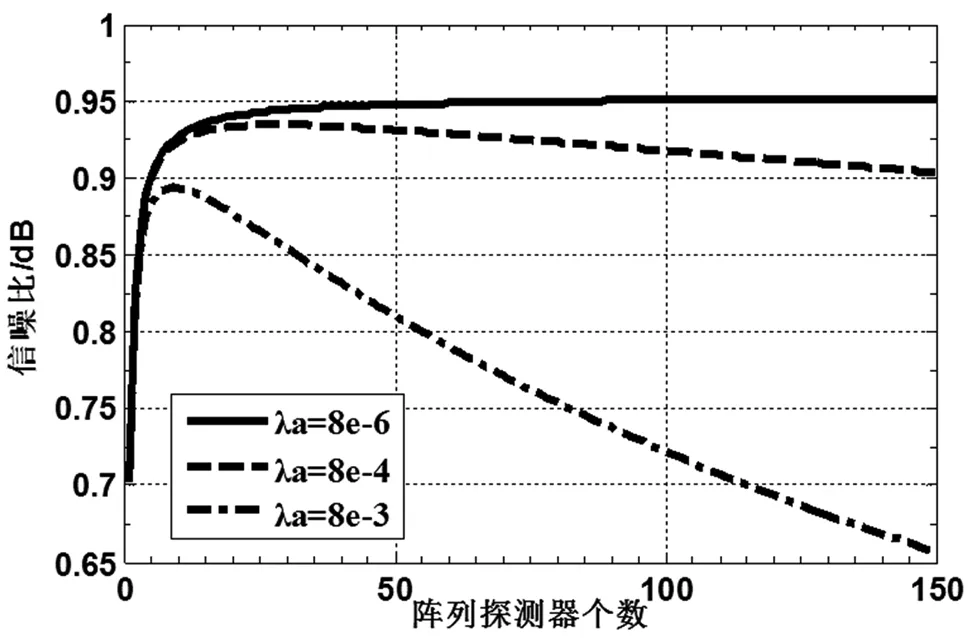
图3 单个门内暗计数不同情况下,信噪比随探测器阵列GM-APD个数m的变化
4 结 语
本文根据单个GM-APD触发模型,推导了基于GM-APD阵列的光子计数通信系统的信噪比公式,分析了不同系统参数对信噪比的影响。数值仿真结果表明,当接收到的信号光较弱时(少于2个/门),增加信号光功率能明显改善系统信噪比;但随着信号光的增强,信噪比会趋于平稳,所以无法一直通过增加信号光功率来提高系统信噪比。增加信号周期内开门次数能有效改善系统信噪比,但其代价是系统通信速率的降低。此外,GM-APD的暗计数会随着探测器阵列的增大而不断累积,过大的GM-APD阵列会带来信噪比的急剧恶化;增大探测器阵列带来系统信噪比的增益,会随着阵列的增大而趋于平缓。在GM-APD暗计数大于8×10-4个/门,较小的阵列不但能简化系统而且具有更好的性能。
