干扰条件下卫星通信链路计算模型研究*
2018-10-15刘冠邑张海勇
刘冠邑,张海勇,任 重
(海军大连舰艇学院 信息系统系,辽宁 大连116018)
0 引 言
卫星通信具有通信距离远、传输容量大、组网灵活等优点。但是,由于电磁波曝露在自由空间,使得卫星通信易被干扰,尤其是当星上应用不具备抗干扰能力的透明转发器时,干扰对通信的影响更加严重[1]。在无干扰时,卫星通信执行严格的功率控制,确保透明转发器工作在线性区域。但是,实际中卫星通信可能受到来自上行链路或下行链路的干扰。当存在上行干扰时,随着干扰功率的逐渐加大,转发器会从线性状态进入到非线性状态,甚至是饱和状态,从而对通信产生影响。
现有针对卫星通信干扰性能的研究各有侧重。文献[2]侧重研究了转发器工作于非线性区时不同干扰样式的干扰性能,但未研究干扰对通信性能的影响;文献[3]侧重研究了转发器工作于线性区和饱和区的干扰性能,但在饱和区仅将转发器增益视为某一经验值,未考虑干扰功率对转发器增益的影响。考虑到实际应用中上行干扰与下行干扰均会存在,且随着上行干扰功率逐渐增大,转发器会遍历各种状态,以上研究不能直接适用于实际干扰条件下的链路性能研究。针对上述问题,本文将研究转发器工作在各个工作状态时的功率条件,得出不同上行干扰功率范围下的转发器增益,并研究下行干扰对通信性能的影响,在此基础上得出干扰条件下的链路计算模型,为卫星通信中通信抗干扰问题的研究提供理论依据。
1 干扰条件下的透明转发器性能研究
卫星透明转发器只起到功率放大和频率变换的作用,其功率放大主要利用行波管放大器(TWTA)。TWTA具有如下特性:当输入功率小于线性工作点功率时,功放工作在线性区域,功率增益恒定;当输入功率介于线性工作点功率与饱和工作点功率之间时,随着输入功率的逐渐增大,功率增益减小,且增益衰减速率逐渐增大;当输入功率大于饱和工作点功率时,输出功率恒定,此时随着输入功率继续增大,功率增益会以恒定的衰减速率迅速减小。TWTA的功率特性如图1所示。
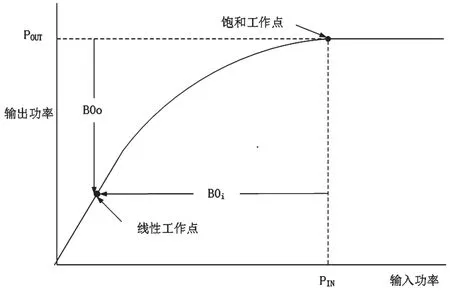
图1 TWTA功率特性
在频分多址(FDMA)卫星通信网络中,载波所占用的功率资源与频率资源相匹配。当载波输入功率小于线性工作点功率时,载波不会对其他链路造成影响[4]。当上行干扰功率较小时,总输入功率小于线性工作点功率,卫星转发器增益恒定。线性工作点的输入功率Pinline为:

其中SFD为转发器饱和通量密度,BOi为转发器输入回退。又因为天线有效面积Ae与卫星接收天线增益Gs存在数学关系:

其中λ为载波波长。所以,式(1)化简后有如式(3)所示的分贝形式:
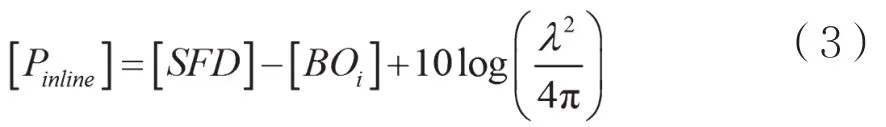
线性工作点的输出功率Poutline计算公式为:

其中EIRPss为卫星饱和全向辐射功率,BOo为输出回退,分贝形式计算公式为:

可以求得透明转发器工作在线性状态时的功率增益G:

将式(3)、式(5)带入式(6),可求出透明转发器的线性增益。
当干扰功率继续增大,输入功率大于线性工作点时,则转发器工作于非线性状态。此时,输入功率大于预分配的最大功率,受干扰的载波会侵占其他载波的功率资源,且功放特性呈现非线性,功率增益逐渐减小,可以利用Saleh模型求得转发器增益。Saleh模型是描述行波管放大器(TWTA)非线性特性的常用形式,幅度—幅度特性表示为[5]:

因为功率与幅度的平方存在线性关系,则可得转发器工作在非线性区域的转发器增益:

其中,输入功率Pin=Cin+Jin,为转发器输入载波功率Cin与转发器输入干扰功率Jin之和;Pout为输出功率。将线性工作点和饱和工作点带入式(8),可求出参数α、β,从而得到转发器工作在非线性状态时的功放特性。线性工作点可由式(3)、式(5)求得,饱和工作点输出功率Poutsat为EIRPss,输入功率由式(9)可求:
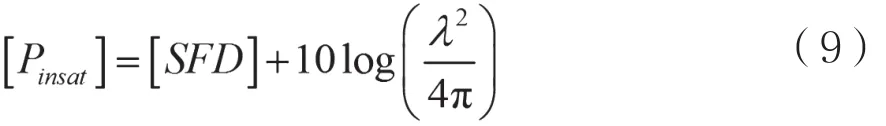
当输入功率大于饱和点输入功率时,转发器工作于饱和状态,输出功率恒为EIRPss,功率增益G小于1,且随着输入功率增大增益逐渐减小。此时,所有载波均会受到干扰引起的信号压缩效应和互调噪声的影响。饱和状态的功率特性为:

其中Pi为饱和时非线性引起的互调噪声功率,其计算公式为[6]:

当等幅、等间隔载波通过行波管放大器时,一般取γ=5.38。可知,此时的互调噪声功率仅与上行载波功率、转发器增益以及输出回退值有关。将式(11)带入到式(10),可以得到此时的转发器增益G为:

由式(12)可以看出,随着卫星接收的干扰功率Jin逐渐增大,转发器增益逐渐减小,即上行功率的压缩程度随着干扰功率增大而增大。
综上所述,在已知转发器输入载波功率Cin的情况下,卫星转发器增益G与转发器输入干扰功率Jin的关系为:

式(13)中相关参数已在上文给出,α、β则可由函数拟合得到。
2 干扰条件下的链路计算模型研究
在卫星通信中可能存在上行干扰,也可能存在下行干扰,甚至二者同时存在。为了分析干扰条件下的链路性能,必须建立综合分析上、下行干扰的计算模型。通常,可利用载波噪声干扰比C/X来表征干扰条件下的链路性能:
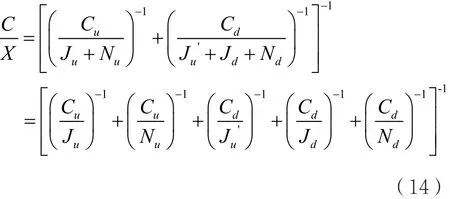
其中,Cu与Cd分别为上行载波功率与下行载波功率;Ju与Jd分别为上行干扰功率与下行干扰功率;Ju´为接收端接收到的转发后上行干扰功率;Nu与Nd分别为上行链路噪声功率与下行链路噪声功率。干扰条件下的C/X计算流程,如图2所示。
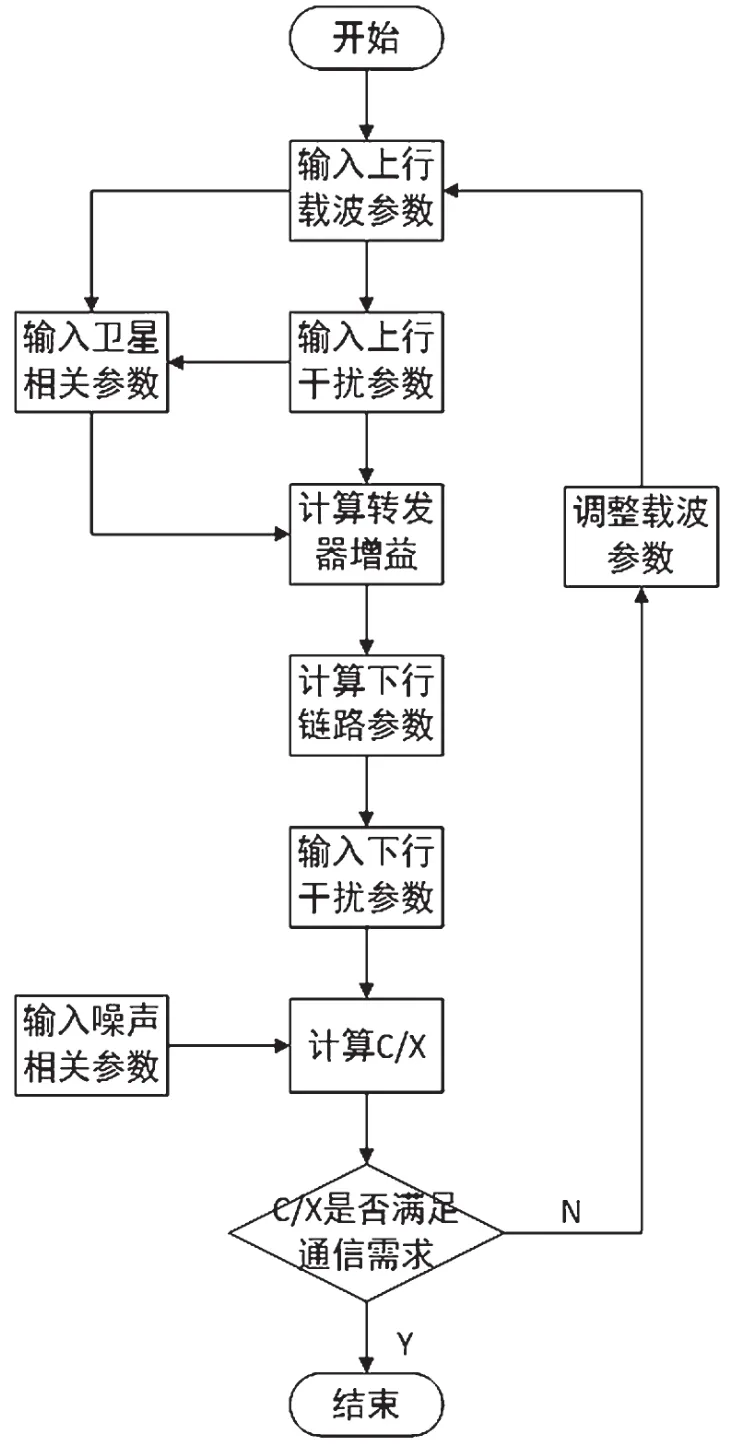
图2 链路计算流程
该模型能够计算存在上行或下行干扰甚至二者同时存在情况下的链路载波噪声干扰比C/X。下面为分析不同类型干扰对链路性能的影响,只考虑存在上行或下行中一种类型干扰的情况。
2.1 上行干扰条件下的链路计算模型
透明转发器抗干扰能力差,当卫星应用透明转发器时,上行干扰不仅会对载波信号产生影响,还会通过影响转发器性能来间接影响通信质量。当只存在上行干扰时,式(14)中的Jd=0,此时链路计算公式可化简为:

式(15)中的上行链路载波功率Cu可由式(16)求得:
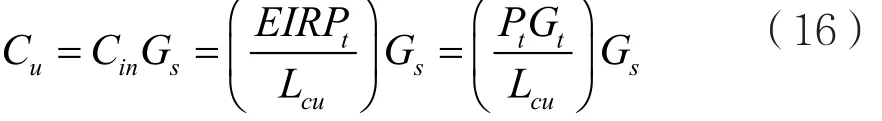
其中Gs为卫星接收天线增益;Cin为转发器输入载波功率;Lcu为载波上行链路损耗;EIRPt为发信站全向辐射功率,可通过发信机功率Pt,与发射天线增益Gt求得;天线增益Gt可由天线效率η、天线口径,工作频率f以及发射天线馈线损耗LFTX计算得到:

同理,可通过上行干扰机功率Pju、干扰机增益Gju与干扰信号上行链路损耗Lju,求得转发器输入干扰功率Jin,进而求得上行干扰功率Ju:

需要注意,相较于人为干扰,自然因素造成的链路损耗对通信影响很小,所以在干扰性能分析中忽略自然因素的影响。此时,载波信号与干扰信号的链路损耗即为自由空间损耗。
自由空间损耗计算公式为:

其中R为传输距离,f为载波频率,光速c=3×108m/s。
下行链路载波功率计算公式为:

同理,可知接收机接收的干扰功率Ju´为:

其中Lcd为载波下行链路损耗;Lju´为转发后干扰信号的下行链路损耗;Gr为收信站接收天线增益,可利用式(17)求得;卫星转发器增益G需要分情况进行分析。当转发器输入干扰功率Jin不同时,转发器增益G发生变化,可利用式(13)进行计算。
在计算噪声功率时,噪声带宽即为载波带宽Bn,则有上行噪声功率为:

下行噪声功率为:

其中k为玻尔兹曼常数,Ts、Tr分别为卫星接收天线与收信站天线的噪声温度。
由式(16)~式(21)计算得到的参数,可以得到:
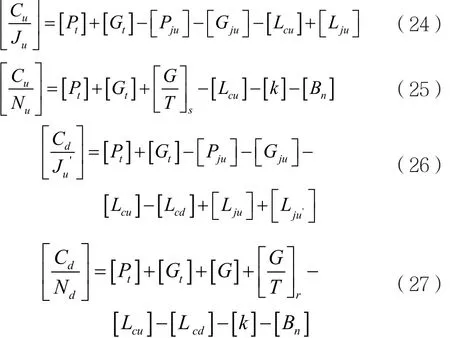
其中(G/T)s与(G/T)r分别为卫星接收天线与收信站天线品质因数,玻尔兹曼常数[k]=-228.6 dBW·Hz,载波带宽Bn可由式(28)求得:

其中载波带宽与滚降系数α、码速Rb、编码效率Cr以及调制方式等因素相关。
将式(24)~(27)带入式(15),可求得当存在上行干扰情况下的总载波噪声干扰比。
2.2 下行干扰条件下的链路计算模型
卫星通信发信站通常执行严格的功率控制,以确保星上转发器正常工作。当卫星通信下行链路受到干扰时,转发器不会受到影响,仍然工作在线性区域。当仅有下行干扰时,式(14)中的==0,此时计算公式可化简为:
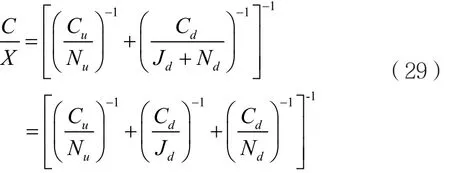
其中的参数Jd、(Cu/Nu)、(Cd/Nd)算法与上文相同。需要注意,此时转发器工作状态与干扰功率无关,仅取决于上行载波功率,转发器增益可由式(13)求得。
下行干扰的链路计算关键在于下行链路干扰功率Jd的计算。下行干扰一般采用机载干扰机对收信站进行干扰。由于接收天线对准卫星,载波信号始终从主瓣进入,天线对载波信号增益恒为Gr。主瓣宽度可由信号波长λ与天线口径D求得:

但干扰机与天线的相对位置不断变化,当干扰信号与接收天线主瓣存在夹角时,天线对干扰信号的增益减小。根据《GB13615-92地球站电磁环境保护要求》规定,干扰信号入射角α与干扰信号增益Gjr的关系为:

在此基础上,可以得出下行链路载波干扰功率比计算公式为:
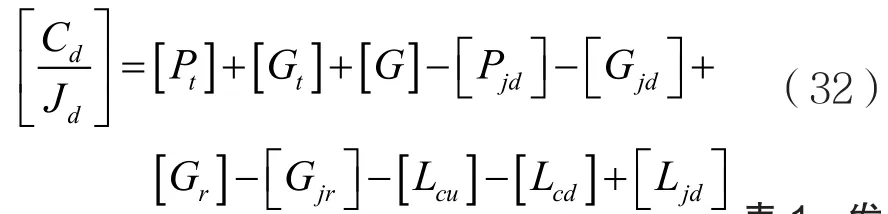
将式(25)、式(27)、式(32)带入式(29),可求得下行干扰条件下的总载波噪声干扰比。
3 干扰性能分析
3.1 上行链路干扰性能分析
在对卫星通信上行链路干扰时,一般采用大功率地基干扰机。上行干扰优势在于干扰机功率增益大,直接影响转发器性能且影响范围广。但是,由于干扰机与卫星距离远,会使干扰信号受到较大损耗。本文以噪声干扰为例,研究上行干扰功率与干扰性能的关系。
在发信站A与收信站B的通信中,相关通信参数参照文献[7]中的通信实例,分别如表1~表3所示。
当系统采用QPSK调制方式,1/2卷积码编码方式,滤波器滚降系数为0.3时,发信机发送速率为2 Mb/s,功率为1 dBW的载波信号。此时,计算可得链路性能相关参数如表4所示。

表1 发信站A相关参数
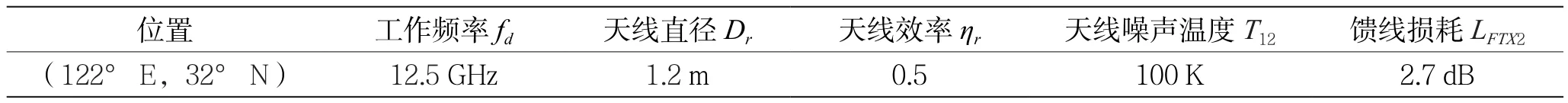
表2 收信站B相关参数

表3 中卫10号卫星转发器相关参数

表4 链路性能相关计算结果
当地基干扰机位于(110.5°E,20°N),天线增益为50 dB,干扰信号频率与上行载波频率一致时,可以得到干扰上行链路损耗Lju=208.0 dB,干扰下行链路损耗Lju´=Lcd=207.0 dB。通过计算可得,转发器处于线性工作点时的干扰功率为17.1 dBW,转发器处于饱和点时的干扰功率为23.5 dBW。上行干扰功率与转发器增益存在的关系如图3所示。
图3显示,当干扰功率小于17.1 dBW时,转发器增益恒定。当干扰功率在17.1 dBW与23.5 dBW之间时,转发器增益逐渐减小。当干扰功率大于23.5 dBW时,转发器增益迅速减小。将转发器增益G带入式(27),可以得到上行干扰条件下的载波噪声干扰比C/X与干扰功率Pj的关系如图4所示。
在干扰功率较小时,上行干扰对卫星通信性能影响较小。当干扰功率超过-10 dBW后,随着干扰功率烦人继续加大,载波噪声干扰比迅速减小,链路性能恶化严重。当干扰功率在0 dBW左右时,C/X已经降低到门限值以下。此时,尽管转发器仍工作在线性区域,干扰并未对转发器性能造成影响,但该卫星通信系统已经无法保证正常通信。

图3 上行干扰功率与转发器增益曲线

图4 上行干扰功率与链路性能曲线
3.2 下行链路干扰性能分析
对卫星下行链路的干扰一般采用机载干扰方式,这种干扰方式的覆盖范围小,适合对确定目标进行干扰。因为距离干扰目标近、传输损耗小,所以机载干扰功率无需过大就能够满足实际需求。下行干扰性能主要取决于干扰机功率、干扰信号波束与主瓣夹角以及干扰信号传输距离。其中,干扰功率取决于干扰机工作情况,干扰信号波束与主瓣夹角、干扰信号信号传输距离可根据干扰机与收信站相对位置确定。
仍以发信站A与收信站B之间的通信为例,分析下行链路干扰对通信性能的影响。当机载干扰机与收信站B距离8 km,喇叭天线增益为8 dB,干扰信号频率与下行载波信号相同时,可得此时干扰信号传输损耗为132.5 dB。由式(31)可以确定,存在不同干扰信号入射角时,接收天线对干扰信号的增益Gjr如表5所示。

表5 干扰信号入射角与增益关系
将相关参数带入式(32),计算得出此时下行载波干扰比Cd/Jd。此时,上行链路不受干扰的影响,转发器正常工作在线性区域,此时转发器增益G由式(13)求得为186.4 dB,可由式(25)、式(27)计算的出上行链路载噪比Cu/Nu与下行链路载噪比Cd/Jd。将相关参数带入式(29)可得载波噪声干扰比C/X与下行干扰功率Pjd的关系如图5所示。
图5结果表明,下行干扰信号入射角α对下行干扰性能影响显著。随着入射角的不断增大,干扰性能下降,即要达到相同的干扰效果,入射角大的干扰信号需要更大的功率。这是由于入射角增大,干扰信号从旁瓣进入接收天线,此时天线对干扰信号增益减小。同时,通过对比图4、图5可知,在对卫星通信链路进行干扰时,要达到相同的干扰效果,下行干扰所需干扰功率更小。这一结论与实际“下行干扰距离目标近,所需功率较小”的事实相符。
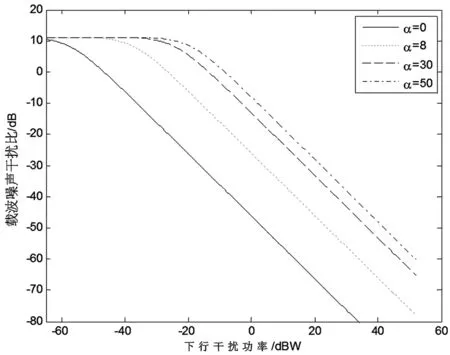
图5 下行干扰功率与链路性能曲线
4 结 语
本文提出了一种干扰条件下卫星通信链路计算模型,综合考虑了上行干扰情况与下行干扰情况,其中当通信链路受到上行干扰时,模型给出了不同转发器工作状态对应的功率范围与转发器增益,进而求得载波噪声干扰比来表示链路性能;当存在下行干扰时,模型研究了干扰信号入射角与干扰性能的关系。基于以上链路计算模型的研究,本文最后利用发信站A与收信站B间的通信实例,分析了上行干扰与下行干扰的性能,得出结果符合实际情况,验证了链路计算模型的可行性,说明本文提出的链路计算模型能够应用于干扰条件下的链路性能分析中。本文提出的链路计算模型,能够计算不同干扰条件下的链路性能参数,可用于评估链路性能,也可以预测抗干扰效果,为通信抗干扰技术的应用提供参考指标。
