基于点扩散函数估计长曝光大气湍流图像复原
2018-10-15徐丹青安博文赵明
徐丹青,安博文,赵明
(上海海事大学信息工程学院,上海 201306)
0 引言
大气湍流退化图像恢复技术是在遥感、天文观测及远程监视领域中的重要步骤之一。由于大气环境中的湍流无处无在,因此光学成像系统的成像效果受到极大的影响。
根据成像系统曝光的时间长短,大气湍流退化图像大致可分为两类:长曝光大气湍流图像和短曝光大气湍流图像。长曝光大气湍流图像的退化特征为整体模糊,退化点扩散函数近似为高斯模型。短曝光大气湍流图像的退化特征为畸变和光照不均匀。
在自然条件下,我们一般很难获取清晰图像的先验知识和退化点扩散函数。所以估计点扩散函数是一个复杂的问题。
本文中以大视角、远距离条件下的长曝光大气湍流退化图像为研究对象,提出了一种点扩散函数的估计方法。首先,根据高斯函数模型建立长曝光大气湍流退化图像的点扩散函数框架,然后,通过对自然图像的频谱特征分析,建立了近似频谱原点对称的模型,在该模型的基础上,结合退化图像的频谱构建清晰图像的频谱,再通过改进拟合方式获得了点扩散函数的参数,最后利用维纳滤波获得了复原图像。
1 点扩散函数估计方法
图像退化模型可表示为如下:
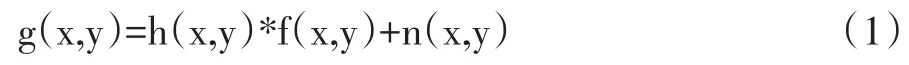
式中:g(x,y)为退化图像;f(x,y)为初始图像;h(x,y)为大气湍流的点扩散函数,将公式(1)转换到频域上,即可表示为:
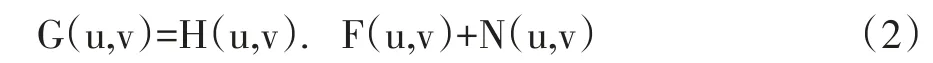
式中:G、H、F、N 分别为 g、h、f、n 的傅里叶变换。
当光学成像系统的曝光时间较长比如达到几秒至几十秒,则记录的是一个时间平均像,即为长曝光大气湍流退化图像,其传递函数H(u,v)可表示为:

波前相位空间结果函数可表示为:

r0为大气相干长度,将波前相位空间结果函数(4)代入式(3)可得:


将公式(6)代入公式(5)中,可以得到基于r0的长曝光退化函数为:


进一步简化可得到:


由上式可以看出,长曝光大气湍流退化系统可以看成是一个高斯分布,α是由大气介质中湍流强度等环境因素决定,β是长曝光大气湍流退化系统的参数。
由公式(2)各个分量分别取模,再将公式两边分别除以max( ||G(u,v))以进行归一化,可得到:
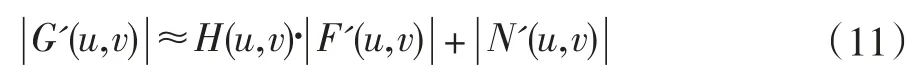
假设环境中的噪声对成像系统的影响较小(忽略噪声影响)且满足下列条件:
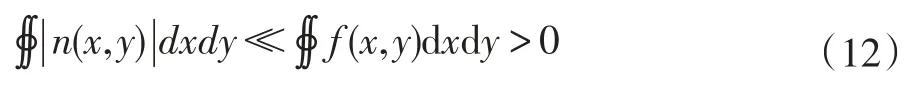
则频谱归一化模型可以近似看成:

将推导的长曝光大气湍流退化系统的传递函数(7)代入(13),然后再将两边取自然对数得:
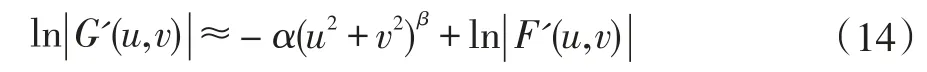
因为原图像和大气湍流的点扩散函数的频谱具有对称性,所以可让u=0,可得到如下结果:
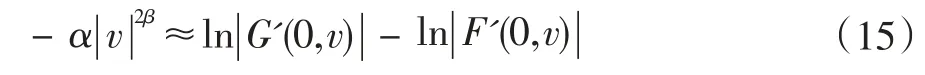
只要得到α的值就可以计算出点扩散函数,因此,获取点扩散函数的关键就在于构建ln ||F'(0,v)。APEX算法将ln ||F'(0,v)项看作常数,研究表明其取值在(2,6)范围内效果最佳。本文针对于复杂背景的自然图像采用了“近似频谱原点对称”的模型对ln ||F'(0,v)进行充构建,一次来估计点扩散函数。
2 复杂背景下远距离自然图像大气湍流退化前后频谱特征
研究人员在分析远距离自然图像频谱特征的过程中得出一个统计规律,即在自然图像的傅里叶变换空间坐标轴上,如果采用双对数坐标显示,自然图像的频谱最佳拟合曲线有着相似的斜率。
本文选取的自然图像是成像系统在远距离条件下获取的,具有背景复杂,纹理信息丰富,几何线条多样化的特点,其中图1的(a)为清晰的自然图像,(b)为清晰图像频谱取用正半轴数据且在双对数坐标系下的显示。根据频谱可发现,中低频段几乎是斜线下降。

图1 清晰图像及频谱
根据前文的分析,由于长曝光的大气湍流退化过程可以表示为清晰图像和点扩散函数的卷积,因此本文对此类退化过程进行模拟。
图2位远距离自然图像在长曝光大气湍流退化前后的频谱对比。
其中(a)为清晰图像,(b)为退化后的图像。经过大量模拟实验可知,经过大气湍流后的退化图像,其频谱要整体低于清晰图像,且高频部分变化更加明显,远距离拍摄的图像,其频谱在退化之前的中低频段几乎为一条直线,类似一个轴对称三角形。

图2 退化前后对比
经过前文的分析可知,在远距离条件下获取的自然图像,其频谱特征具有很大的相似性。通过对比退化前后的图像频谱特征,就可以通过退化图像频谱来恢复出清晰图像频谱。
3 频谱模型重建和点扩散函数估计
3.1 频谱模型重建
在取 β=5 6,的情况下,可以通过公式(15)估计出α的值,但要想获得点扩散函数的参数α,还必须要知道退化之前的清晰图像频谱ln ||F'(0,v)。由于自然图像在退化前后的频谱在高频部分变化不明显,在中低频的部分被压低,且在远距离获取的自然图像频谱在中低频段几乎为直线,所以我们可以利用这些特点重建清晰图像频谱ln ||F'(0,v),以此来估计α的值。
图3所示为长曝光大气湍流退化的自然图像频谱,我们假设图像的尺寸为2M×2N,我们用图中所示的直线来表示ln ||F'(0,v)中低频段部分,由于图像频谱关于坐标轴原点对称,所以我们只需要关心0<v<N部分。
假设直线定点和右端点分别为A和B,根据退化图像获取直线AB的数据,假设A,B两点的分别为直线AB方程为y=ax+b,两点坐标可表示为:

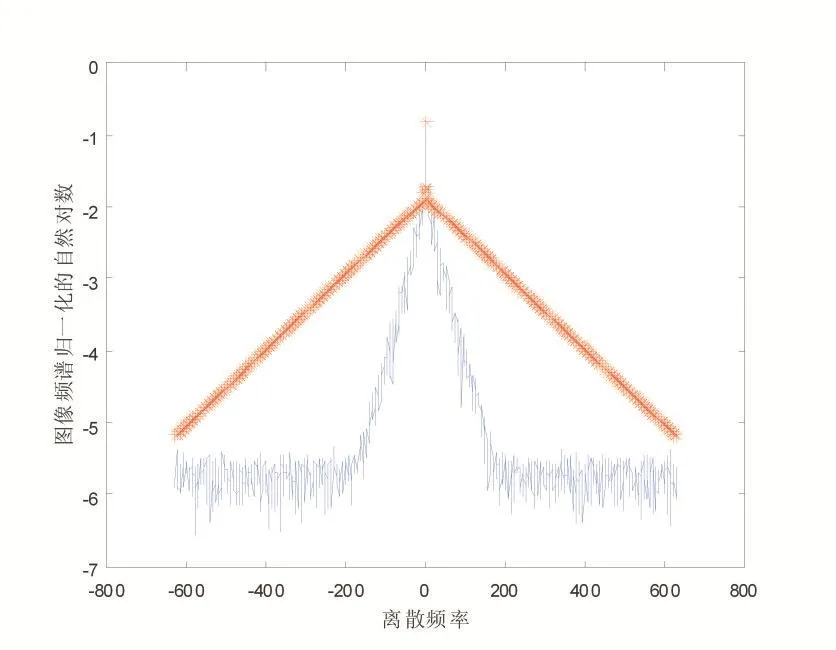
图3 频谱重建
在上式中:参数n1,n2主要用于确定点A和点B,在本文的研究背景下,我们取n1≥0,n2≤10。为了保证重建过后的清晰图像频谱要整体高于退化图像的频谱,我们设置参数σ1≥-1和σ2≤1。得出的点A和点B的坐标确定直线AB的方程,这样就可以确定AB上的每一个点的值。按照公式(19)就可以确定清晰图像频谱

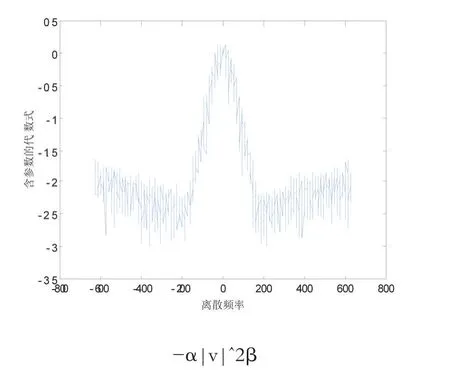

图4 选取有效区间
3.2 点扩散函数估计
(1)传统最小二乘法

最小二乘方拟合要求各个误差的平方和最小即:

其中Δmin代表误差值δi平方之和的最小值。

上式求出α的值可以比较好地拟合实验数据,此种方法即为传统最小二乘法原理。
(2)曲线拟合方法改进
对于公式(21),重新定义其最佳拟合应为:

对上式求导得:

由公式(24)求出α,从而y=-α ||x2β为改进的曲线拟合结果。
4 图像复原步骤及结果分析
4.1 实验步骤
(1)获取长曝光大气湍流退化图像;(2)分析退化函数,并根据分析,取 β=5 6;(3)根据频谱特征重建模型ln ||F'(0,v)并估计出参数α;(4)使用维纳滤波复原。
4.2 图像复原结果
本实验选取了三组图像,图5为输入的三组退化图像,图6分别为APEX算法复原的图像,其估计的参数α=0.000587,图7分别为本文提出的改进算法结合改进拟合算法估计点扩散函数的复原图,其估计的参数α=0.000723。

图5 退化图像

图6 APEX算法

图7 本文改进算法
4.3 结果评价
在对实验结果进行分析的过程当中我们使用灰度平均梯度值(GMG)和拉普拉斯梯度值(LS)最为客观的评价标准。GMG是求图像中各个像素点在x和y方向上的灰度差值的均值平方和,GMG值越大表明图像的纹理越清晰,图像的质量越好。LS是图像中每个像素在3×3的领域内在拉普拉斯算子作用下归一化均值。LS值越大表明图像的轮廓越清晰,图像的质量就越好。GMG和LS的计算公式如下:
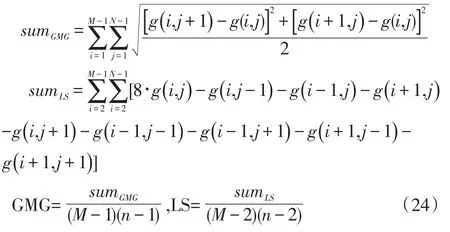
式中:g为待评价图片,尺寸为M×N。
实验结果显示:本文的算法可以较为准确地估计出点扩散函数,在主观评价上有较好的视觉效果。表1和表2进一步表明在结合改进的拟合算法的情况下,本文的算法可更进一步复原出远距离长曝光大气湍流图像。

表1 退化图像和复原图像的GMG值
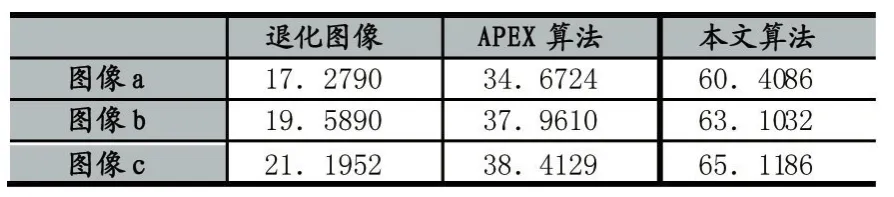
表2 退化图像和复原图像LS值
5 结语
本文针对远距离长曝光大气湍流退化的自然图像进行,分析了其退化点了扩散函数的一般形式,并通过分析其退化前后的频谱特征,估计出了其点扩散函数参数,通过对拟合算法的改进,在主观上获得了较好的视觉效果,在客观评价上也证实了其有效性。
