一种提高捷联惯导系统动基座初始对准精度的方法
2018-10-15赵政,刘冰
赵 政,刘 冰
(1.天津航海仪器研究所,天津300131;2.北京航天控制仪器研究所,北京100039)
0 引言
初始对准是捷联惯导系统的关键技术,捷联惯导系统进入导航工作状态前必须先进行初始对准工作,获取系统初始姿态,初始对准精度直接影响系统导航精度。初始对准过程分为粗对准、精对准两个阶段。捷联惯导系统粗对准的目的是给后续的精对准过程提供较精确的姿态初始值,目前粗对准阶段适用的方法很多,主要包括基于静基座的传统的解析式粗对准和适用于动基座的基于惯性凝固系的粗对准[1⁃3]。 文献[1]对传统解析式粗对准方法静基座下的对准精度进行了详细分析,并得出了具体系统误差评估公式。传统的解析式粗对准方法在干扰不大的静基座条件下,均能取得较好的对准结果,但在实际工程应用中载体不能静基座启动情况下,这种方法存在一定的局限性。文献[2]、文献[3]提出了一种基于惯性凝固系的粗对准方法,该方法从理论上消除了载体角运动干扰对对准精度的影响,并在转台摇摆试验中进行了初步验证。但工程实践应用中,载体运行过程不仅包含角运动干扰,还包含线运动带来的干扰,文献中针对线运动干扰抑制过程并没有进行详细介绍。
本文以惯性凝固系粗对准为基础,详细推导惯性凝固系粗对准算法流程。在目前的方法可抑制载体角运动干扰基础上,针对船载设备动基座机动条件,通过误差分析,提出一种抑制载体线运动干扰的方法,并通过实际数据仿真,应用于系统初始对准过程中。该方法对减小系统粗对准误差,进而提高系统导航精度有一定帮助。
1 坐标系定义
文中所涉及的坐标系定义如下:
(1)地心惯性坐标系(i系)
oxi轴在赤道平面内且指向春分点,ozi轴指向地球自转方向,三轴构成右手坐标系。
(2)地球坐标系(e系)
oxe轴在赤道平面内且指向中央子午线,oze轴沿地球自转方向,三轴构成右手坐标系。e系与地球固连,e系相对于i系的转动角速率即为地球自转角速率ωie。
(3)导航坐标系(n系)
采用东北天坐标系作为导航坐标系。
(4)载体坐标系(b系)
载体坐标系是原点位于惯性组件中心右前上直角坐标系。
(5)初始时刻惯性坐标系(i0系)
在初始对准起始时刻(即当t=t0=0时),oxi0轴在当地子午面内且平行于赤道平面,ozi0轴指向地球自转方向,三轴构成右手坐标系,初始对准开始后i0系三轴方向相对惯性空间保持不动。
(6)初始时刻地球坐标系(e0系)
原点为地球中心,oxe0轴在赤道平面内且指向初始对准开始时刻的当地子午线,oze0沿地球自转方向,三轴构成右手坐标系。e0系也与地球固连,并且e0系与i0系之间方位关系是前者只绕后者的ozi0轴转动了ωiet角度。
(7)初始时刻导航坐标系(n0系)
把初始对准开始时刻的导航坐标系定义为n0系,它相对地球表面固定不动,即不随捷联惯导在地球表面运动而运动。
(8)初始时刻捷联惯导惯性坐标系(ib0系)
在t0时刻ib0系重合于b系,初始对准开始后ib0系不随捷联惯导转动,即在惯性空间中保持指向不变。
2 惯性凝固系粗对准算法
目前,船用设备应用的粗对准方法是基于惯性凝固系的粗对准方法[2⁃3], 具体算法如下:
(t)求解过程如下所示:
λ0和L0分别为对准起始t0时刻捷联惯导的经度和纬度,λt和Lt分别为开始对准t时刻的实时经度和纬度, 将式(3)~式(6)代入式(2), 经过合并整理,最终得到计算公式, 如式(7)所示。
(t)求解过程为:
式(8)中,利用陀螺输出的角运动信息,通过捷联惯导姿态更新算法,可以实时求得矩阵即:
求解过程可依据惯性误差比力方程,将实时重力矢量gn和经补偿后的fb在惯性系i0和ib0下投影计算得到, 具体公式如式(10)所示,vib0(t)、ui0(t)求解过程如式(11)、 式(12)所示。
惯性凝固系粗对准方法,其实质就是从加速度计信息fb中有效分离出重力信息gb, 将其投影到惯性系ib0下,并将地理系下的gn投影到惯性系i0下,二者构造出惯性凝固系之间的变换关系求取再通过外部信息和陀螺输出计算变换关系,进而由式(1)求出载体姿态矩阵
从上述方法可以看出,影响粗对准精度误差源主要包含外参考误差、陀螺误差及加速度计误差。通过仿真,在陀螺、加速度计无误差条件下,外参考位置信息存在±10m定位误差,速度信息存在±0.05m/s的误差,经计算对惯性凝固系下粗对准误差精度影响不足1%,从仿真分析可以得出,外部参考信息误差对粗对准精度影响较小。因此,陀螺、加速度计自身误差及外部干扰影响惯性仪表产生的误差在粗对准精度中占有比较大的权重。在同等陀螺、加速度计精度条件下,尽可能减小外部环境条件干扰对惯性仪表的影响,也是提高对准精度的一条有效途径。通过仿真分析,加速度计干扰误差特别是动基座条件下,杆臂、载体晃动或机动过程中对加速度计产生切线加速度、向心加速度等干扰加速度信息,对粗对准精度产生很大的影响。 虽然式(11)、 式(12)在计算vib0(t)、ui0(t)过程中采用了积分操作,对载体晃动干扰引起的惯性仪表误差有一定的抑制作用,但由于积分时间限制,特别是对载体航向变化产生切线加速度、向心加速度误差的抑制能力明显不足。这些粗对准期间所产生的误差将影响精对准过程,传导致导航过程影响定位、定向、水平姿态、速度等导航信息精度。
根据文献[1]和文献[7],车载惯性系统外部干扰频率均在0.5Hz以上,船载系统外部干扰频率均在0.2Hz以上,这些干扰频率相对于惯性系统所包含的地球周期、Schuler周期、Foucault振荡周期而言均是非常短的高频信号,据此结论,可以设计适当的低通滤波器滤除系统高频干扰频率,保留系统低频有用信号,理论上可以提高系统对准精度。同时,以某型捷联惯导设备海上试验数据为基础,通过频谱分析,也验证了加速度计干扰信息相对于有用信息均是高频项的判断。因此,基于某型捷联惯导设备海上试验数据,针对加速度计信息干扰信息设计适当的低通滤波,减小载体运动对加速度计的影响,通过数据仿真发现对提高粗对准精度有一定帮助。
3 滤波器设计
目前,数字滤波器的设计主要包括有限冲击响应FIR滤波和无限冲击响应IIR滤波。相对于惯性系统,由于实现0.2Hz以下的低通滤波器的设计工作已属于窄带滤波器设计范畴,若使用有限冲击响应FIR滤波器,需要上千阶方可实现,将产生很大的相移,计算量大,不利于适应动基座惯性对准过程;而无限冲击响应IIR滤波,具有阶次低计算量小等优点。因此,选取阶次低计算量小的IIR滤波器,设计低通滤波器,截止频率设计为 0.15Hz, 40dB 衰减[3]。 滤波传递函数如式(13)所示,系统幅频特性如图1所示,系统阶跃响应、脉冲响应图如图2、图3所示,可以看出系统滤波器设计稳定。
以海上试验某航次单个X加速度计数据为例,将滤波前后数据进行对比,如图4、图5所示。从图4、图5可以看出,滤波后加速度计高频干扰项均已滤除,与设计初衷一致。
4 试验验证及仿真
以海上试验几个航次原始数据为基础,选取码头锚泊、载体行进过程中航向变化约10°、航向变化约45°、航向变化约100°这4种载体不同机动状态3min原始数据进行数据仿真,对应用原始数据和滤波后数据进行粗对准运算,并进行精度对比,如图6~图9所示。其中,蓝色实线为原方法粗对准结果,红色实线为应用滤波后数据进行粗对准结果,黑色虚线为方位参考基准。各种不同状态下,原方式粗对准结果和现方式粗对准结果对比如表1所示。
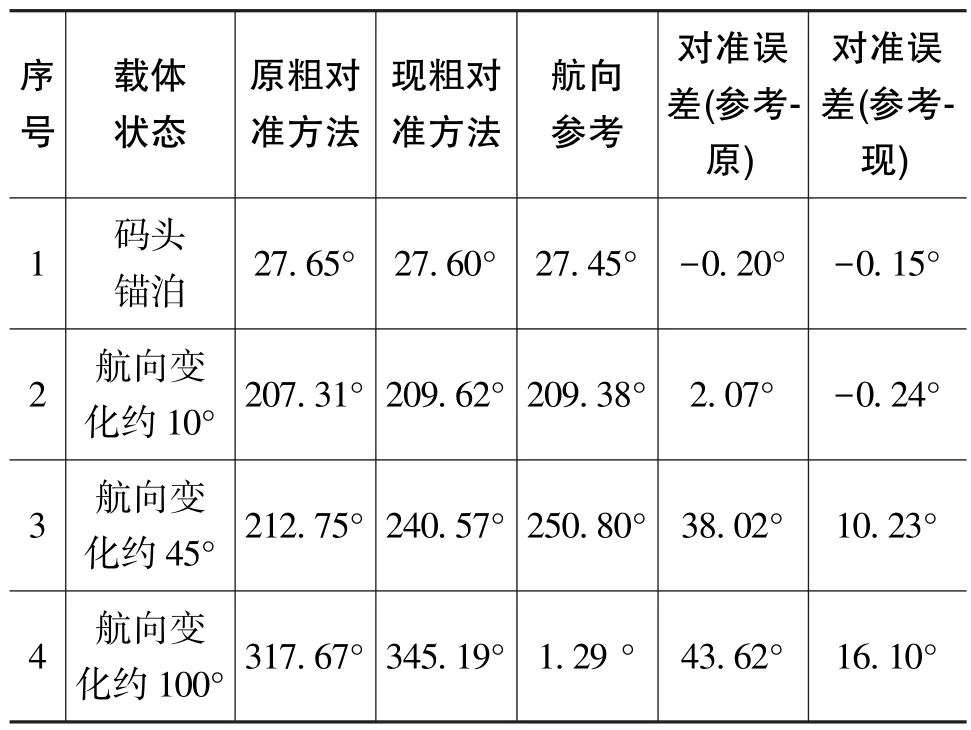
表1 载体不同状态粗对准结果对比Table 1 Comparison of coarse alignment results in different state of carrier
从表1、图6~图9可以看出,无论是对原粗对准方法还是经过滤波后的粗对准方法,载体不同的机动状态将对粗对准结果产生较大的影响,载体行进条件越恶劣,粗对准误差相对越大。同时,在相同的载体运行条件下,将两种粗对准结果与参考信息进行对比,可见经过滤波后的粗对准结果比原粗对准结果在对准精度方面存在一定的改善,说明增加加速度计滤波的方法有益于提高粗对准精度,进而为提高精对准、导航精度打下一定的基础。
选取载体行进过程中航向变化约100°原始数据,分别采用两种粗对准方法进行1h初始对准(含3min粗对准和57min精对准)和1h导航试验进行对比,具体结果如图10所示。其中,蓝色实线为原方法导航结果,红色实线为现方法导航结果。可以看出,精对准后,原粗对准方法1h导航结果综合位置误差约为2nmil,现粗对准方法综合位置误差约为0.45nmil,说明增加对加速度计滤波粗对准方法在载体动基座条件下对提高导航精度具有一定效果[4⁃5]。
5 结论
通过上述试验仿真可以看出,采用低通滤波结合惯性凝固系粗对准方式,在原方法基础上可以进一步消除载体运动过程中给加速度计带来的干扰加速度,对改善粗对准结果有一定益处,进而对提高导航精度有一些帮助,对工程实践应用具有一定指导意义。
