四旋翼飞行器线性自抗扰控制
2018-10-13陈奕梅
汤 帅, 陈奕梅
(天津工业大学电气工程与自动化学院,天津 300387)
0 引言
近年来,随着国内外高校和科研机构加大对四旋翼无人飞行器的研究力度,四旋翼无人飞行器已成为控制领域研究的热点[1]。四旋翼无人飞行器是一种小型的旋翼直升机,拥有稳定的悬停和精确的定点飞行能力,被广泛应用于航拍、情报侦察、电力巡检、消防以及植保等领域,而且能够在复杂和危险的环境中执行任务,具有很高的科研和实用价值。
四旋翼无人飞行器通过控制4个旋翼的转速变换来实现六自由度灵活飞行,仅具有4个控制输入,是一个典型的欠驱动系统,同时具有强耦合、非线性、易受外部干扰等特性[2]。对四旋翼无人飞行器自抗扰控制的研究主要集中在以下几个方面:文献[3]采用非线性自抗扰算法,具有不依赖于精确模型就能够实现对系统总扰动的实时估计和补偿等优点,但是3个组成部分都使用了非线性模块,所以设计参数过多不易确定稳定性边界,容易引起抖动,难以将算法应用于实际;文献[4]采用线性自抗扰算法,参数整定简单,当输入为连续时变且具有噪声信号时,难以解决快速性和准确性的矛盾,同时输出会受到噪声干扰。为了解决以上存在的控制参数过多、抖振、模型不准确、动态性能难以满足等问题,本文采用跟踪微分器与线性自抗扰控制组合的算法对四旋翼无人飞行器系统进行控制,具有不依赖于精确的系统模型、能够实时地对系统内扰和外扰进行估计和补偿等优点,并易于将研究成果应用于实践,具有较高的研究价值。
1 Qball2动力学模型
目前四旋翼无人飞行器分为”十”型和”×”型两种结构,本文采用的是Qball2四旋翼无人飞行器,结构为“十”型。
Qball2四旋翼无人飞行器呈十字交叉结构,4个末端各固定一个电机。1,3号电机顺时针旋转,2,4号电机逆时针旋转。通过控制器调整4个电机的转速可以实现机身的灵活飞行,如图1所示。
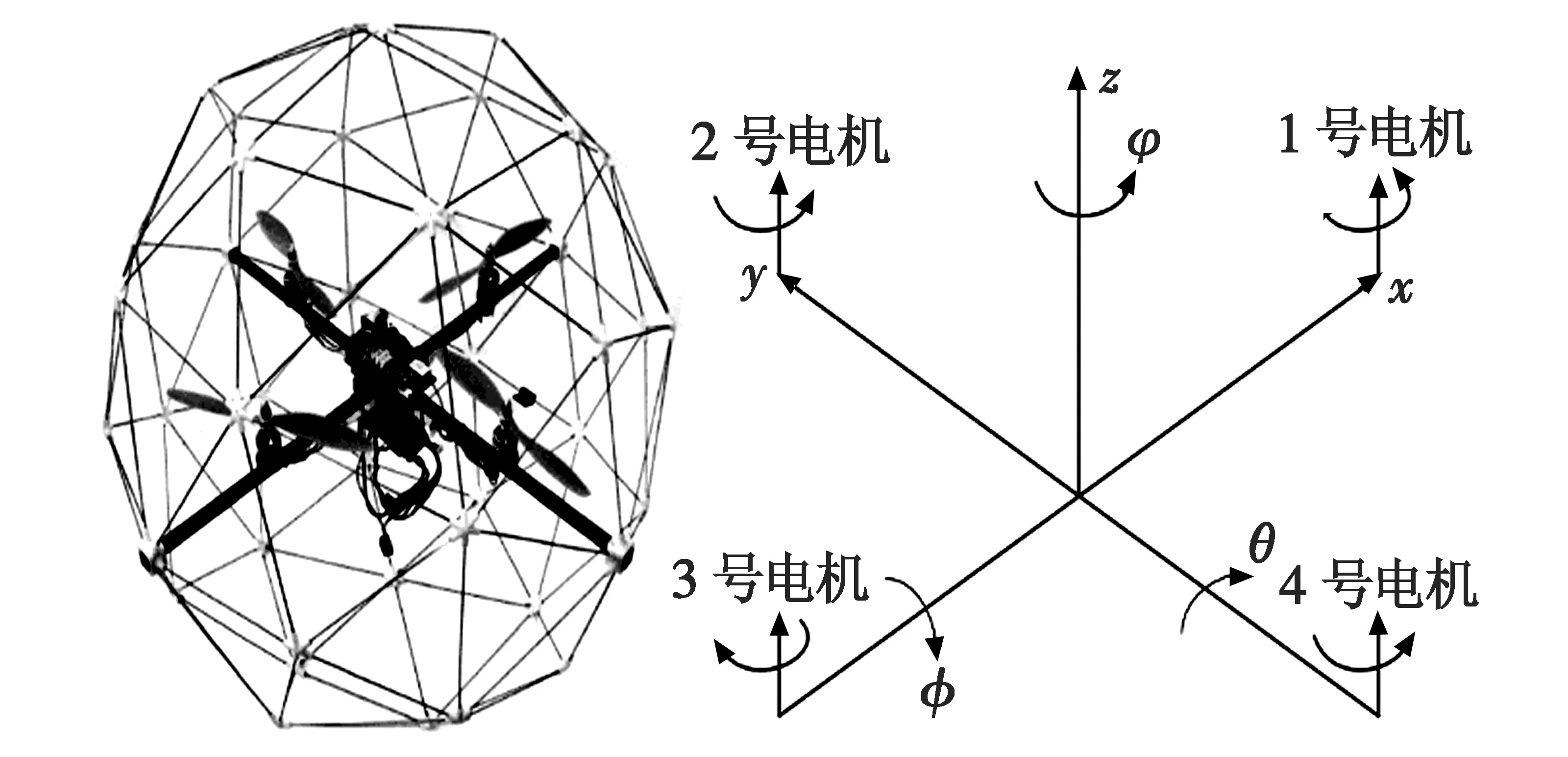
图1 Qball2实物及其工作原理示意图Fig.1 Qball2 and its working principle
假设Qball2的机身为一个结构对称的刚体,考虑到系统未建模部分以及环境不确定的影响,并结合Qball2的结构,得到Qball2四旋翼无人飞行器的动力学模型[5]为
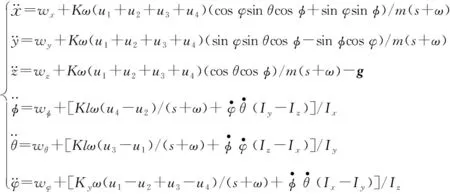
(1)
式中:K为升力系数;Ky为反扭矩系数;ω为带宽;s为复变量;ui(i=1,2,3,4)为第i个电机的PWM输入;φ为滚转角(Roll)、θ为俯仰角(Pitch)、φ为偏航角(Yaw);l为电机中心到机身质心之间的距离;m为机身的质量;g为重力加速度;Ix,Iy和Iz分别为绕x,y和z轴的转动惯量;wi(i=x,y,z,φ,θ,φ)为系统未建模部分和外部干扰的总和。
设定Fi(i=1,2,3,4)为4个输入的虚拟控制量,其与4个直流无刷电机ui(i=1,2,3,4)的关系为
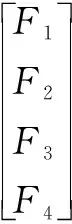
(2)
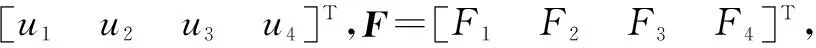
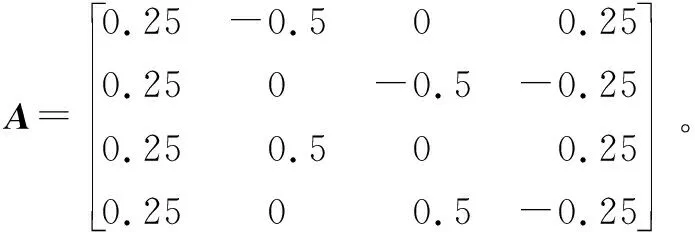
(3)
将式(2)和式(3)代入式(1) ,可得简化后的Qball2四旋翼无人飞行器动力学模型为
(4)
2 自抗扰控制器
自抗扰[6]算法存在参数多难以调节的问题,高志强教授提出一种线性自抗扰算法[7]。传统线性自抗扰算法略去跟踪微分器会降低系统的动态性能,对于这个问题,采用一种跟踪微分器与线性自抗扰结合的控制方法。
2.1 跟踪微分器
跟踪微分器[8]能够解决被控对象的快速性与准确性之间的矛盾。在快速跟踪给定输入和给出质量较好的微分信号的同时降低超调。式(5)是连续形式的跟踪微分器,由二阶最速综合函数[9]构造。
(5)
式中:fhan为二阶离散最速综合函数;r0为速度因子;h0为滤波因子。
因此可以通过调节r0和h0柔化突变的期望输入,提取良好的微分信号。
2.2 线性自抗扰控制器
假设存在如下二阶系统
(6)
进一步可以写为
(7)
式中:a1,a2和b为模型参数;w为系统的未建模部分与外部扰动的总和;b0为补偿系数;u为控制量。
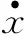
(8)
式中:x1和x2为系统的状态变量;x3为系统扩张状态。据此构造该系统的LESO[10]如下:
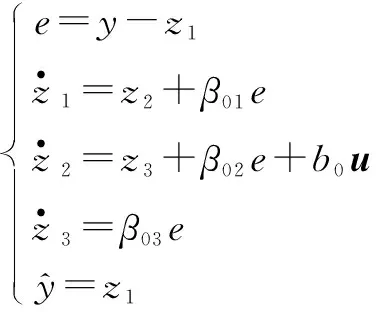
(9)
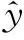
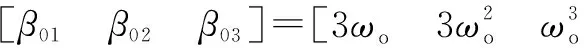
ωo的大小决定了对系统各状态的跟踪速度,LESO可以实现对系统各个状态的实时观测。
LESO对控制量进行实时跟踪补偿,得到的控制量为
(10)

(11)
式中,u0为PD控制器的输出,
u0=kp(x0-z1)-kdz2
(12)
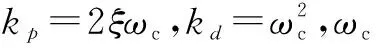
为使系统稳定无超调,令ξ=1,得到ωc>0,又因为系统期望输入和总和扰动有界,所以系统稳定。
三是定主题。主题党日活动通常以“规定动作+”的模式开展,“+”的部分就是结合实际确定的“自选动作”。设计好党日活动主题,做好“自选动作”,是开展好“主题党日”活动的关键之一。在设计党日活动主题时,一是要紧紧围绕党的建设“5+2”的总体布局(全面推进党的政治建设、思想建设、组织建设、作风建设、纪律建设,把制度建设贯穿其中,深入推进反腐败斗争),突出党内政治生活的政治性、时代性、原则性、战斗性。
3 Qball2控制系统设计
四旋翼控制系统没有单独的控制量来控制x和y
两个通道,只能通过控制俯仰和滚转姿态角来实现。将四旋翼控制系统分为内环(俯仰和滚转)和外环两个控制系统[12]。传统的线性自抗扰算法能够满足一般系统的要求,而四旋翼对外环控制系统的快速性和准确性有较高的要求,本文在外环线性自抗扰控制器基础上引入了跟踪微分器。整个控制系统的结构如图2所示。
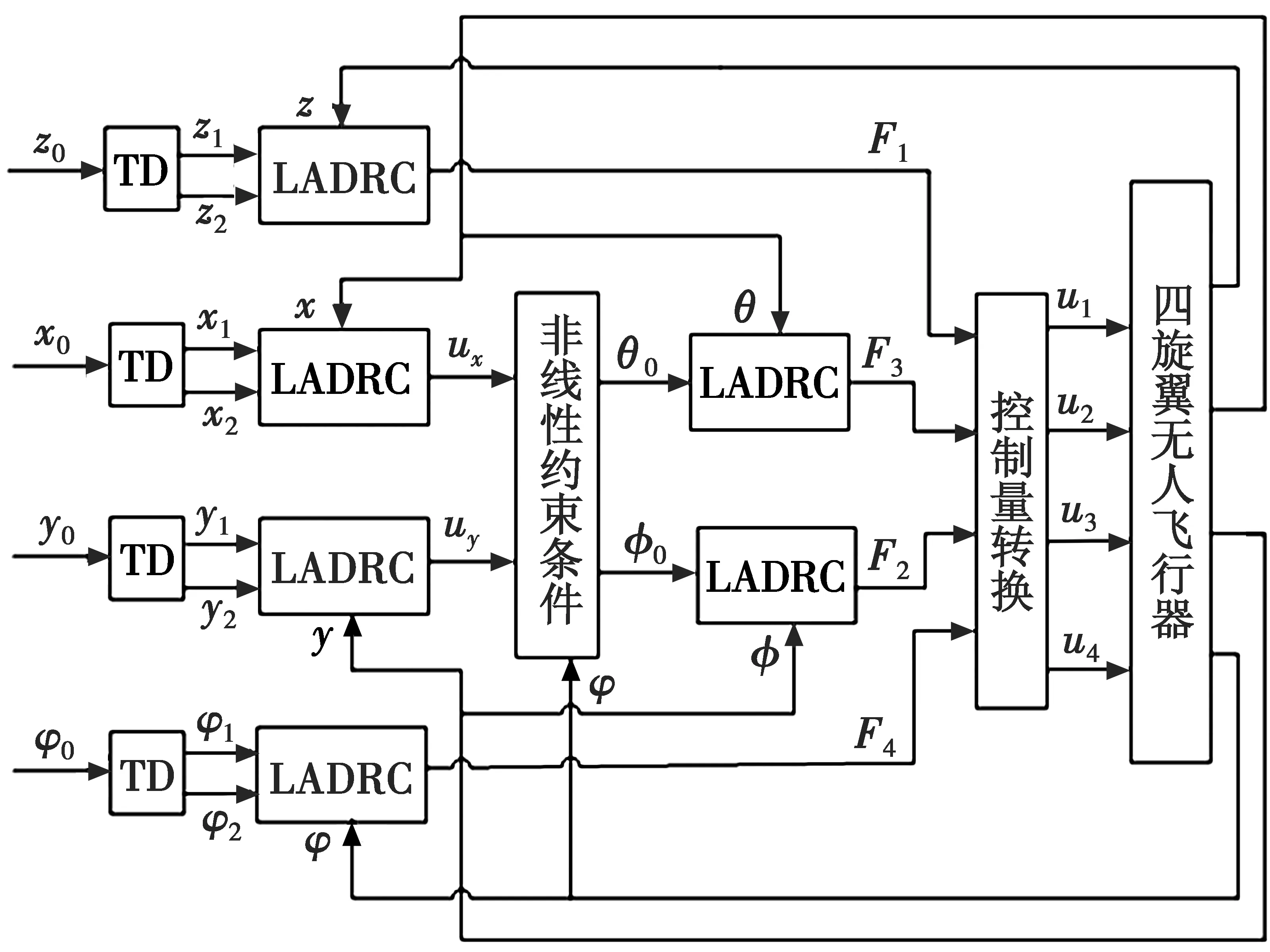
图2 Qball2四旋翼系统控制总图Fig.2 Control chart of Qball2 quadrotor system
3.1 内环LADRC控制器设计
姿态控制[13]是四旋翼控制系统的基础。为了简化控制系统结构,在内环采用传统LADRC控制器。
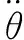
(13)
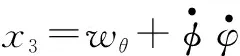
设计俯仰角的LADRC控制器如图3所示。
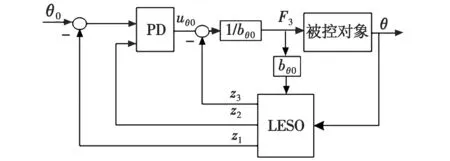
图3 俯仰角控制框图Fig.3 Diagram of pitch angle control
1) 线性扩张状态观测器。
由式(9)和式(13)得到俯仰角的线性扩张状态观测器为
(14)
2) 线性组合环节。
由式(10)和式(12)得到俯仰角的PD控制器的输出uθ 0和控制量F3分别为
(15)
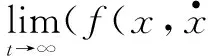
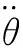
(16)
式(13)被简化成一个串联积分系统,同理可得内环滚转角的LADRC控制器。
3.2 非线性约束条件
由图2可知,内环的期望输入与外环的控制输出存在转换关系。通过对外环x和y控制输出的反解可以得到俯仰角和滚转角的期望输入,外环控制输出和内环期望输入之间存在的非线性约束关系为
(17)
在实际飞行中,俯仰角和滚转角很小,可以进一步简化为
(18)
对其反解可以得到内环姿态的期望输入为
(19)
3.3 外环TD-LADRC控制器设计
对四旋翼控制系统外环的高度,x,y和偏航方向均采用TD与LADRC结合的控制算法。
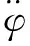
(20)
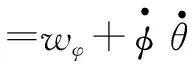
设计偏航角TD-LADRC控制器如图4所示。
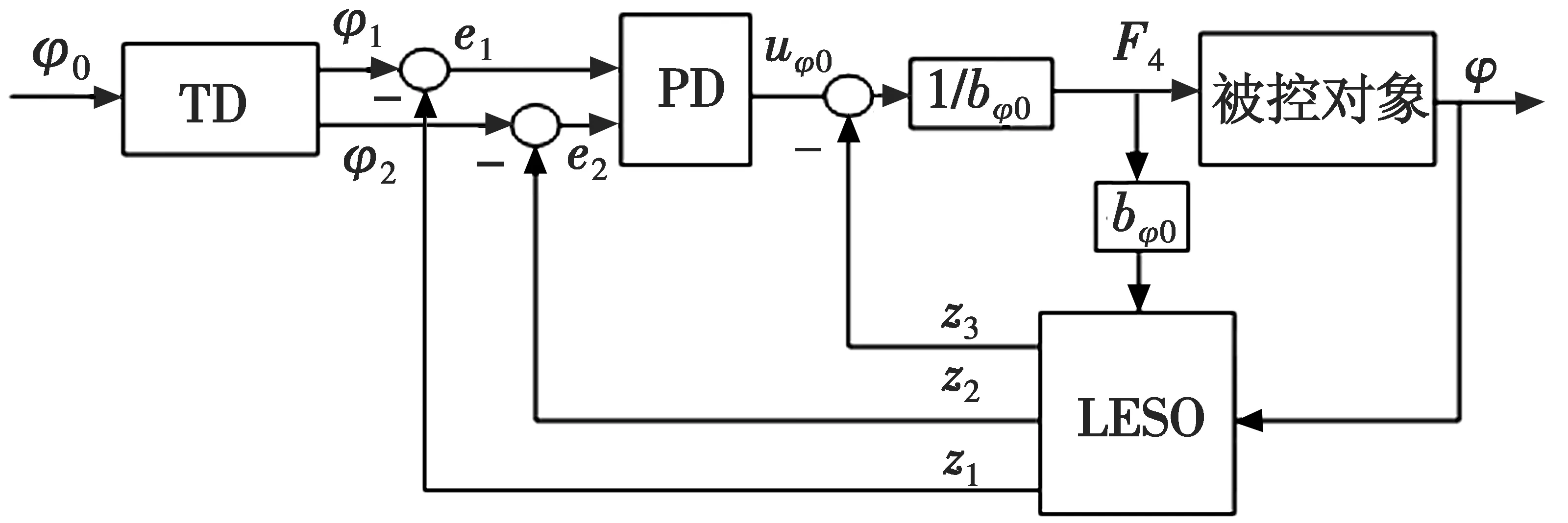
图4 偏航角控制框图Fig.4 Diagram of yaw angle control
1) 跟踪微分器。
根据式(5)得到偏航角跟踪微分器为
(21)
2) 线性扩张状态观测器。
由式(9)和式(20)得到偏航角的线性扩张状态观测器为
(22)
3) 线性状态误差反馈。
由式(10)和式(12)得到偏航角的PD控制器的输出uφ 0和控制量F4为
(23)
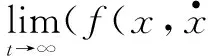
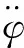
(24)
式(20)被简化成一个串联积分系统,同理可得外环其他通道的TD-LADRC控制器。
4 实验验证
4.1 仿真实验
为验证所设计控制器可以解决快速性和准确性之间的矛盾,与传统LADRC做对比仿真实验,结果如图5~图7所示。
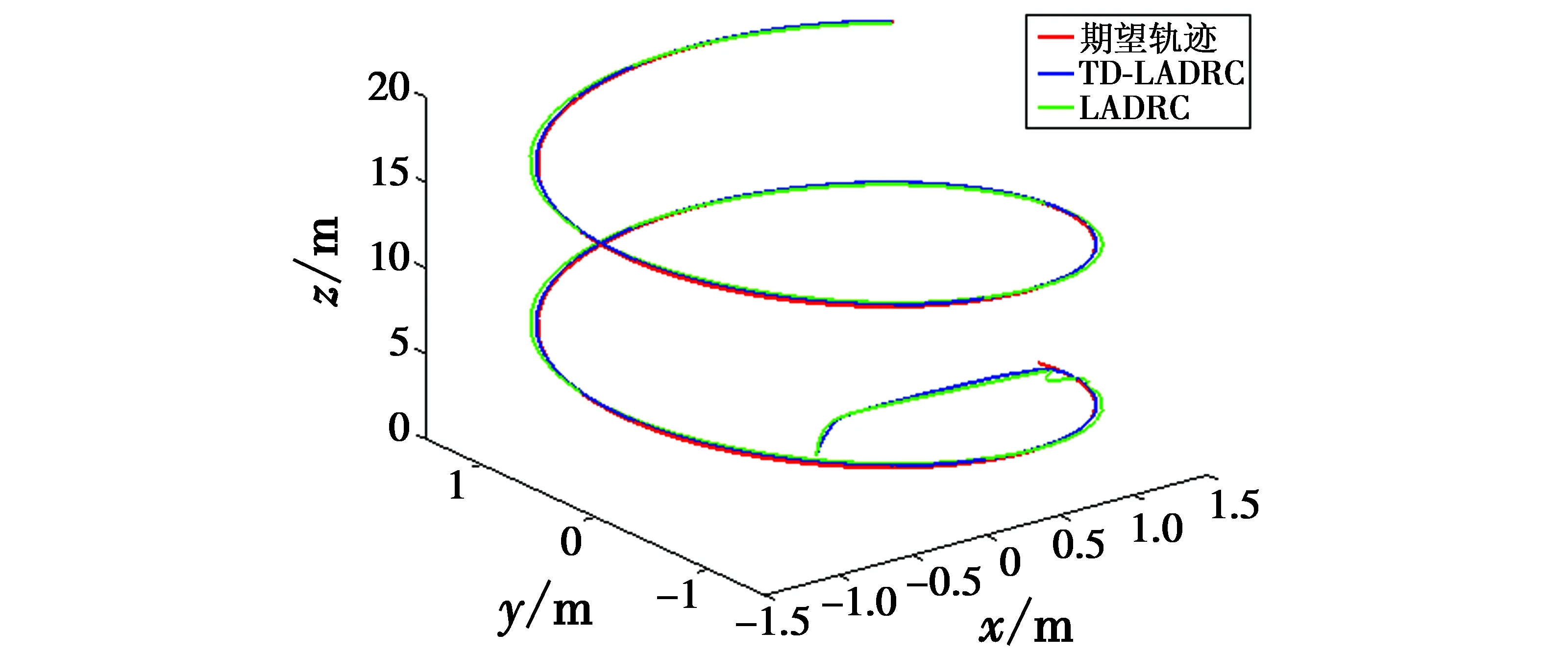
图5 三维轨迹跟踪曲线图Fig.5 3D trajectory tracking curve
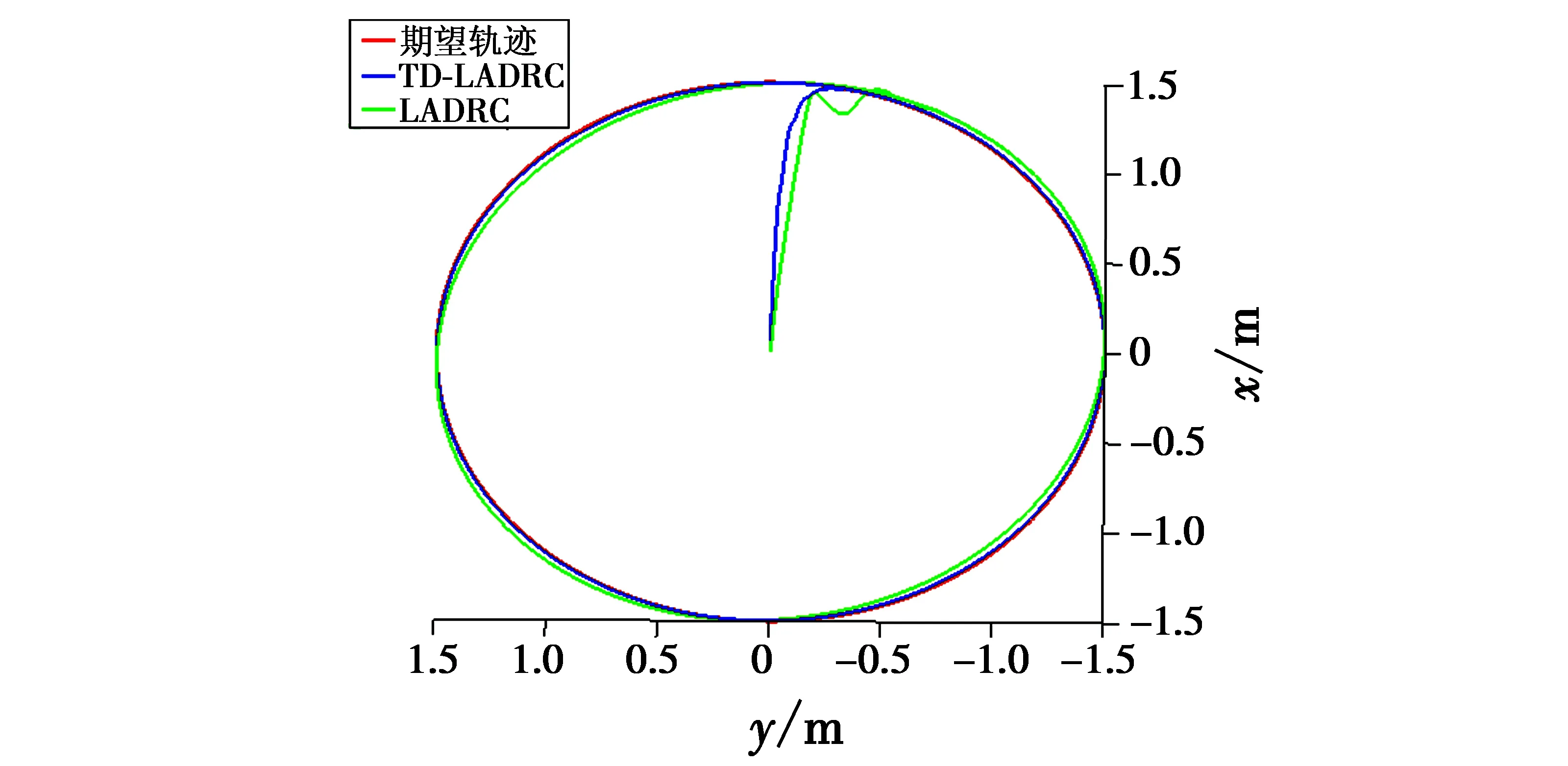
图6 二维轨迹跟踪曲线图Fig.6 2D trajectory tracking curve
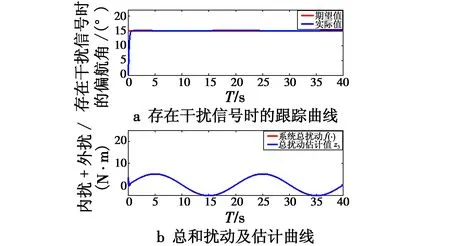
图7 存在干扰信号时偏航角的跟踪曲线Fig.7 Tracking curve of yaw angle under disturbance
Qball2的初始位姿为(y,x,z,φ)=(0 m,0 m,0 m,0°),Qball2的期望轨迹为y=1.5sin(-0.1t),x=1.5·cos 0.1t,φ=0,z=(2+0.15t)。
Qball2模型参数如表1所示。
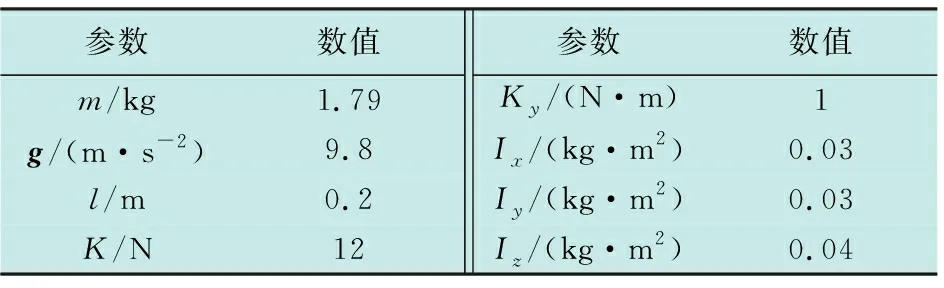
表1 Qball2模型参数
根据文献[14]和[15]的自抗扰控制算法的整定方法,首先初步选定内环姿态的控制器仿真参数,然后选定外环的控制器仿真参数,并经过调试最终参数选择如下:(ωxo,ωxc,bx 0)=(10,2.3,10);(ωyo,ωyc,by 0)=(11,3.6,14);(ωzo,ωzc,bz 0)=(33,11,8);(ωφo,ωφ c,bφ 0)=(35,19,60);(ωθo,ωθc,bθ 0)=(35,19,60);(ωφo,ωφc,bφ 0)=(35,12,90)。
由图5、图6可以得出,TD-LADRC相较LADRC控制器,由于跟踪微分器的作用,当期望值突变时,能降低超调,具有良好的快速性和准确性。
LESO可以对系统的未建模部分和外部干扰进行跟踪和补偿,设定初始姿态(φ,θ,φ)≈(0°,0°,0°),期望姿态(φ,θ,φ)=(0°,0°,15°),对系统增加外部干扰0.2sin(0.1πt)。
由图7可以看到,偏航角的LESO可以对系统总的扰动进行实时跟踪并补偿,得到良好的偏航角输出曲线。
4.2 Qball2平台实验
仿真实验不能完全验证控制器的有效性,为了进一步验证所设计控制器的实用性和优越性,将本文所设计的算法应用于Qball2实验平台。
1) 姿态跟踪实验。
实际自主飞行中,姿态的转动角度很小,为验证所设计内环姿态LADRC控制器的跟踪能力,进行姿态跟踪实验。初始姿态(φ,θ,φ)≈(0°,0°,0°),设定期望姿态(φ,θ,φ)=(15°,15°,0°),时间T的单位为s,可得实验结果如图8所示。
为验证所采用的外环TD-LADRC控制器相较LADRC控制器的优越性,进行了偏航角的对比实验,初始姿态(φ,θ,φ)≈(0°,0°,-3°),设定期望姿态(φ,θ,φ)=(0°,0°,15°),得到实验结果如图9所示。
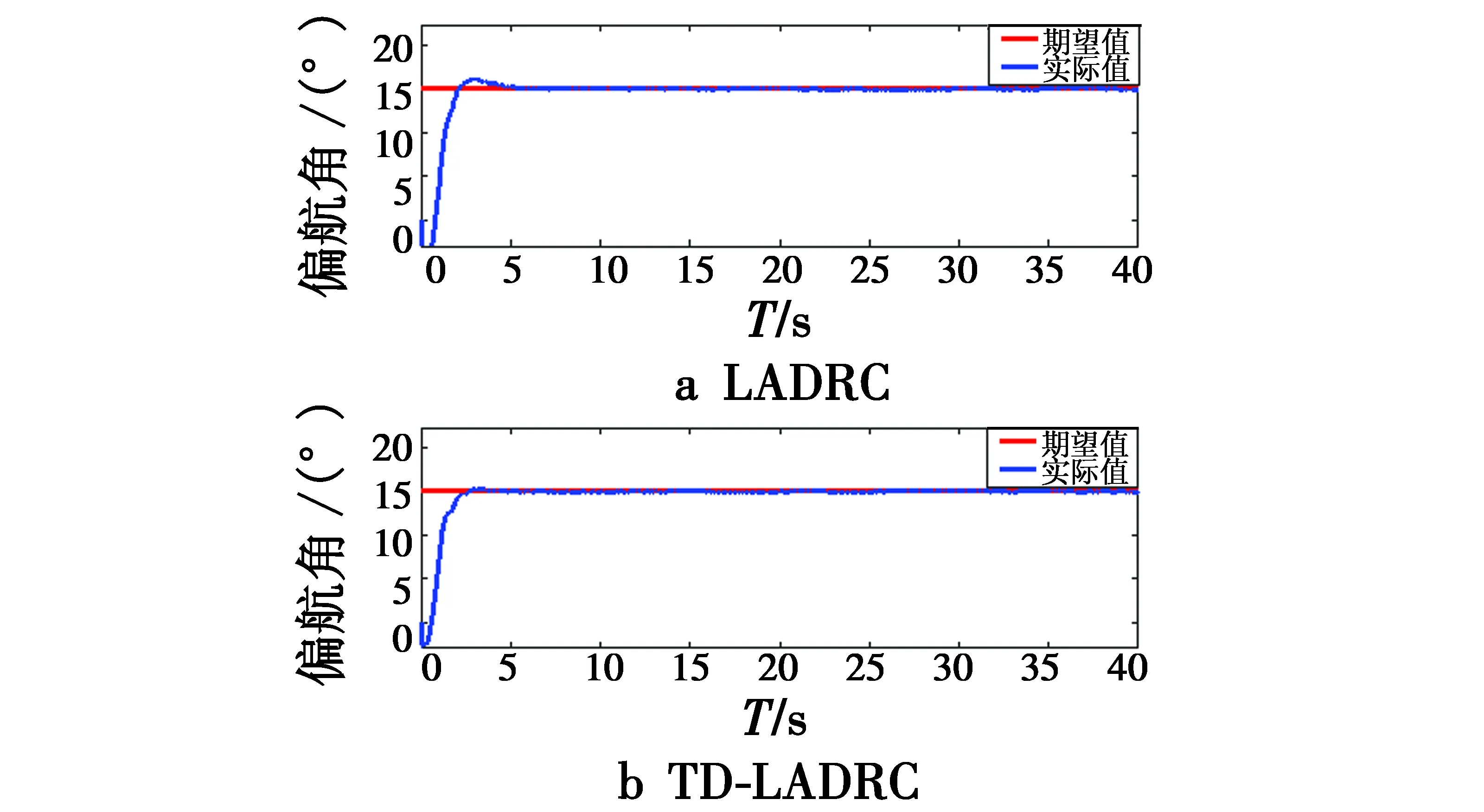
图9 偏航角对比实验曲线图Fig.9 Comparison experiment curve of yaw angle
由图8可以看出,LADRC满足了系统对内环姿态跟踪的要求,图9中TD-LADRC控制器与LADRC控制器相比具有更快的响应速度,满足快速性和准确性的同时,减小了超调。
2) 悬停实验。
实际飞行中,四旋翼飞行器悬停的稳定性很重要,Qball2的初始位姿(y,x,z,φ)≈(0 m,0 m,0.025 m,0°),设定期望位姿(y,x,z,φ)=(0 m,0 m,0.3 m,0°),在37 s左右上位机向Qball2发出下降指令,实验结果如图10~图12所示。
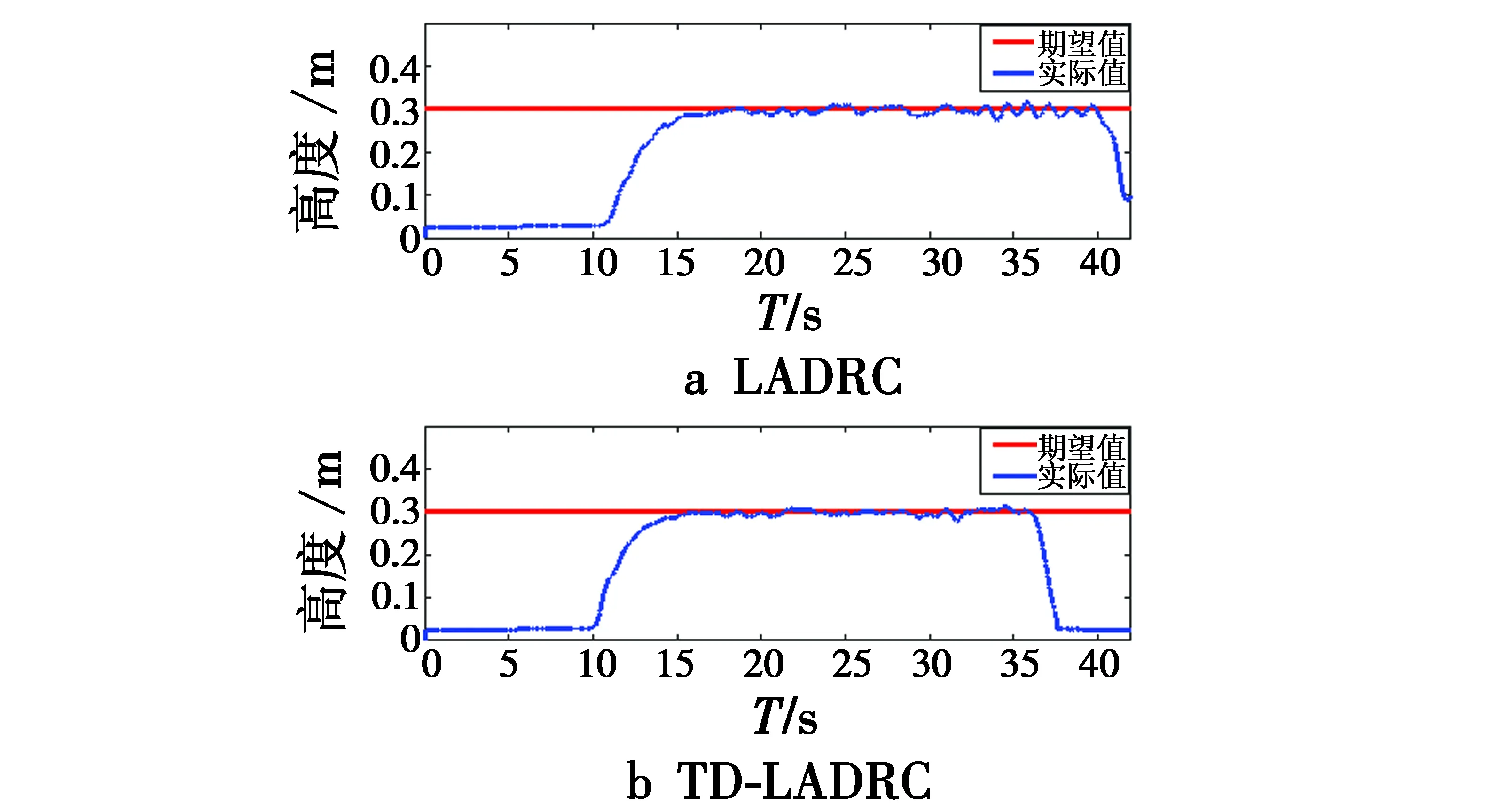
图10 悬停对比实验曲线图Fig.10 Hover contrast experiment curve
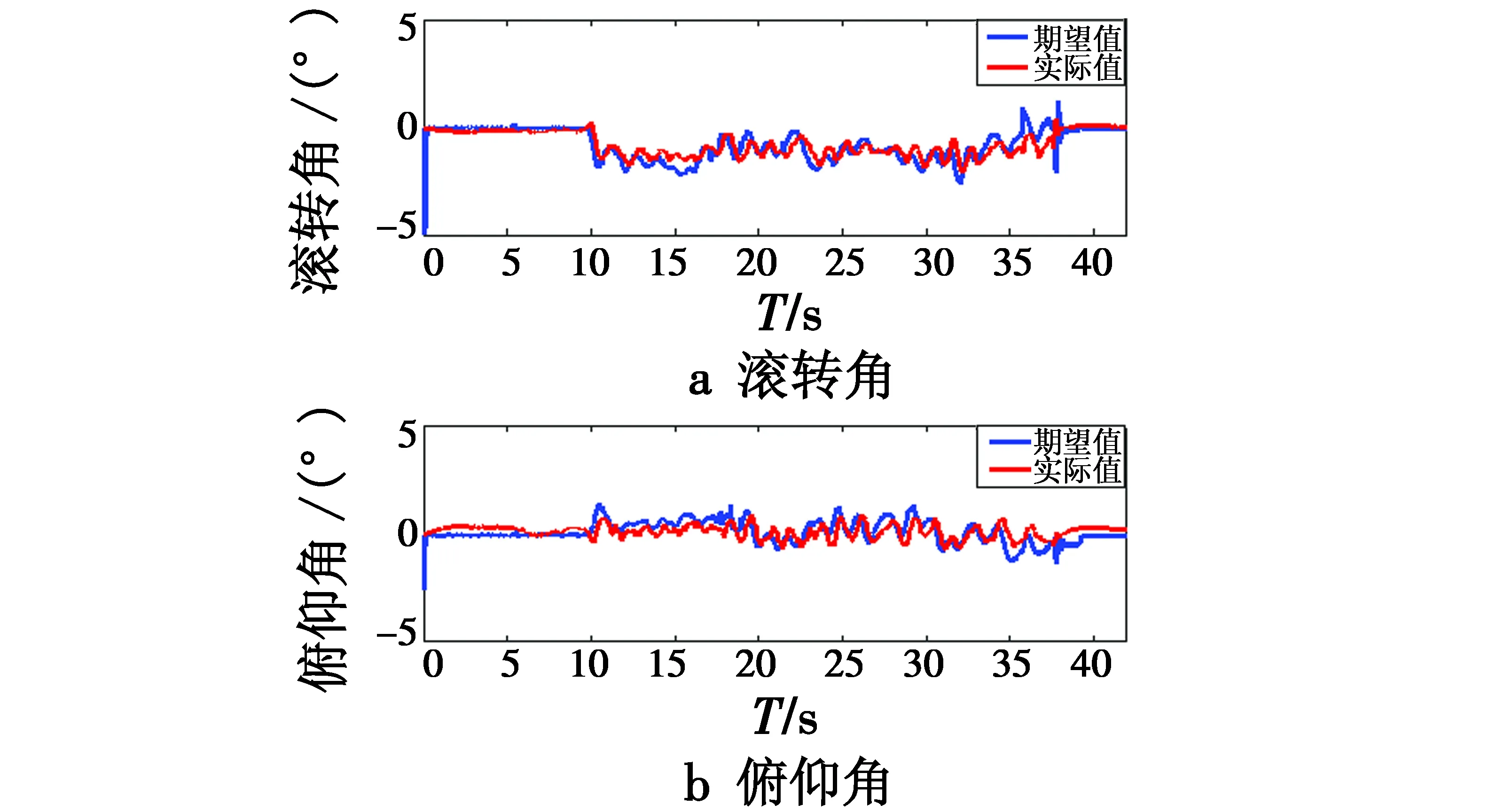
图11 内环姿态响应曲线图Fig.11 Inner loop attitude response curve
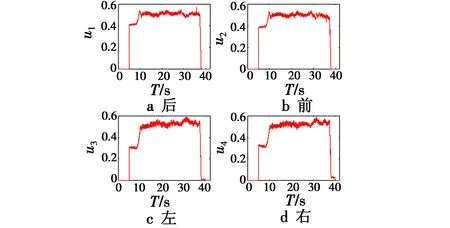
图12 电机PWM输入曲线图Fig.12 Motor PWM input curve
由图10可以看出,TD-LADRC与LADRC相比具有更快的响应速度,其高度误差为±0.019 m。即使在0.3 m的低空悬停,LESO的补偿作用能够减弱旋翼气流以及结构不对称对Qball2的影响。
由图11可以看出,内环姿态LADRC控制器能较好地跟踪期望输入,且期望姿态在±1°变化。
由图12可以看出,当4个电机的PWM输入值达到0.45以上才能保证Qball2离开地面,而且电机PWM输入曲线没有较大波动,也侧面证明了LESO对系统的跟踪和补偿能力,以及系统的稳定性。
5 结论
本文以Qball2无人飞行器为研究对象建立Qball2
的动力学模型,并采用一种跟踪微分器与线性自抗扰结合的控制方法。实验表明所设计的控制器具有响应快速、跟踪准确、鲁棒性强等优点,能够对非线性耦合系统进行良好的控制,验证了控制器的有效性。在未来的工作中,将着手于LADRC抗饱和的研究。
