陀螺稳定平台神经网络滑模变结构控制
2018-10-13鲁延娟李明秋
鲁延娟, 李明秋
(长春理工大学,长春 130022)
0 引言
陀螺稳定平台是一种安装在运动载体上的光电跟踪装置,能够对运动载体所受的扰动进行隔离,并保持平台稳定[1]。在实际应用中,陀螺稳定平台多用于飞机、导弹等场合,这些应用场合决定了陀螺稳定平台应具有很高的快速性和鲁棒性。
目前,实际应用的陀螺稳定平台控制系统多采用PID控制。但是,基于PID控制的各种改进控制方案并不能有效地提高平台的快速性和鲁棒性[2]。针对这个问题,许多研究人员采用现代控制理论对陀螺稳定平台进行控制,已有的文献有些采用了H∞控制[3]和模糊控制方法[4-5]。但这些方法大多需要进行复杂的计算或精确的数学模型,因此很难在实际系统中应用[6]。本文以某吊舱为研究背景,针对其中的陀螺稳定平台速度环控制系统,采用了以神经网络逼近模型的未知部分的神经网络滑模变结构控制方法。仿真实验表明,该控制器的应用有效地提高了陀螺稳定平台的快速性和鲁棒性。
1 陀螺稳定平台系统结构
两轴四框架光电陀螺稳定平台通过陀螺稳定隔离载体的扰动,保证探测器的视轴稳定地指向目标。实现这个控制目标的方法多种多样,但基本上采用的都是机电框架结构。从控制系统的构成来讲,每一个框架都具有相似的结构。一般来说,该框架包括一个内回路速度环和一个外回路位置环[7-8],其结构如图1所示。
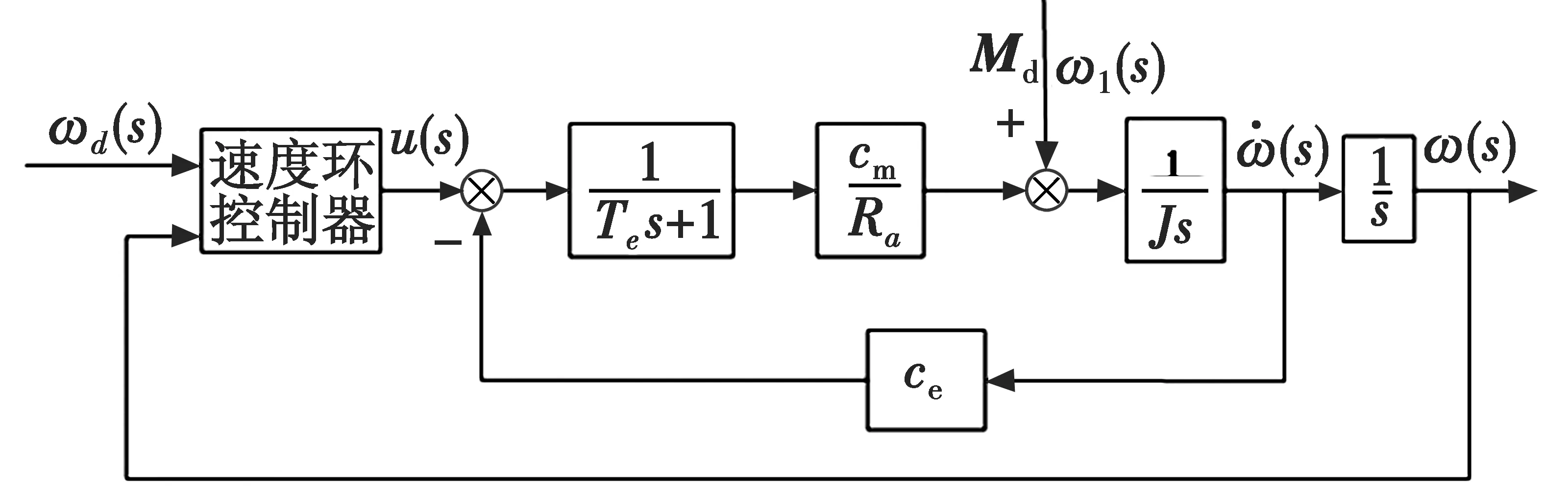
图1 陀螺稳定平台的单轴系统结构图Fig.1 Uniaxial system of gyro stabilized platform
建立系统被控对象的状态方程为
(1)
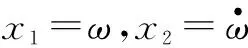
2 陀螺稳定平台速度环控制器设计
2.1 基于指数趋近律的变结构控制器设计
变结构控制理论是一种控制系统的综合方法,适用的控制任务有镇定、运动跟踪、模型跟踪等。它是一类特殊的非线性控制,通过切换函数的方式,迫使系统按预定的“滑动模态”的状态轨迹运动,从而达到系统稳定的目的[9]。
设二阶非线性不确定系统为
(2)
式中:f(·)和g(·)是未知非线性函数;u是控制输入;d(t)为有界干扰。
滑模函数设计为
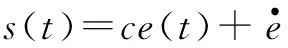
(3)
式中:c>0,满足Hurwitz条件;e(t)=xd-x1(t)。
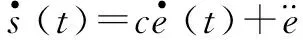
(4)
采用指数趋近律,即
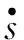
(5)
式中:ε>0;k>0。由式(4)和式(5)可设计控制律为
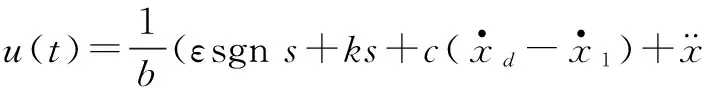
(6)
在式(1)中忽略电感。取R=5 Ω,J=0.3 kg/m2,ce=4.5 V/(rad·s-1),cm=4.17 V/(rad·s-1),r(t)=0.1 sint,扰动取Md=sint。
采用滑模变结构控制(SMVSC)方法,取c=11,ε=0.5,k=15。角位置和角速度跟踪、控制输入u和角度跟踪误差曲线,分别如图2~图4所示。
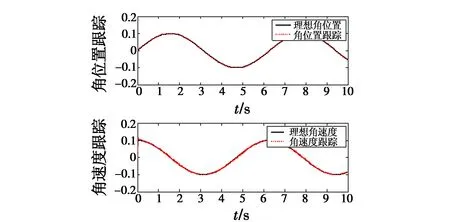
图2 角位置和角速度跟踪(SMVSC)
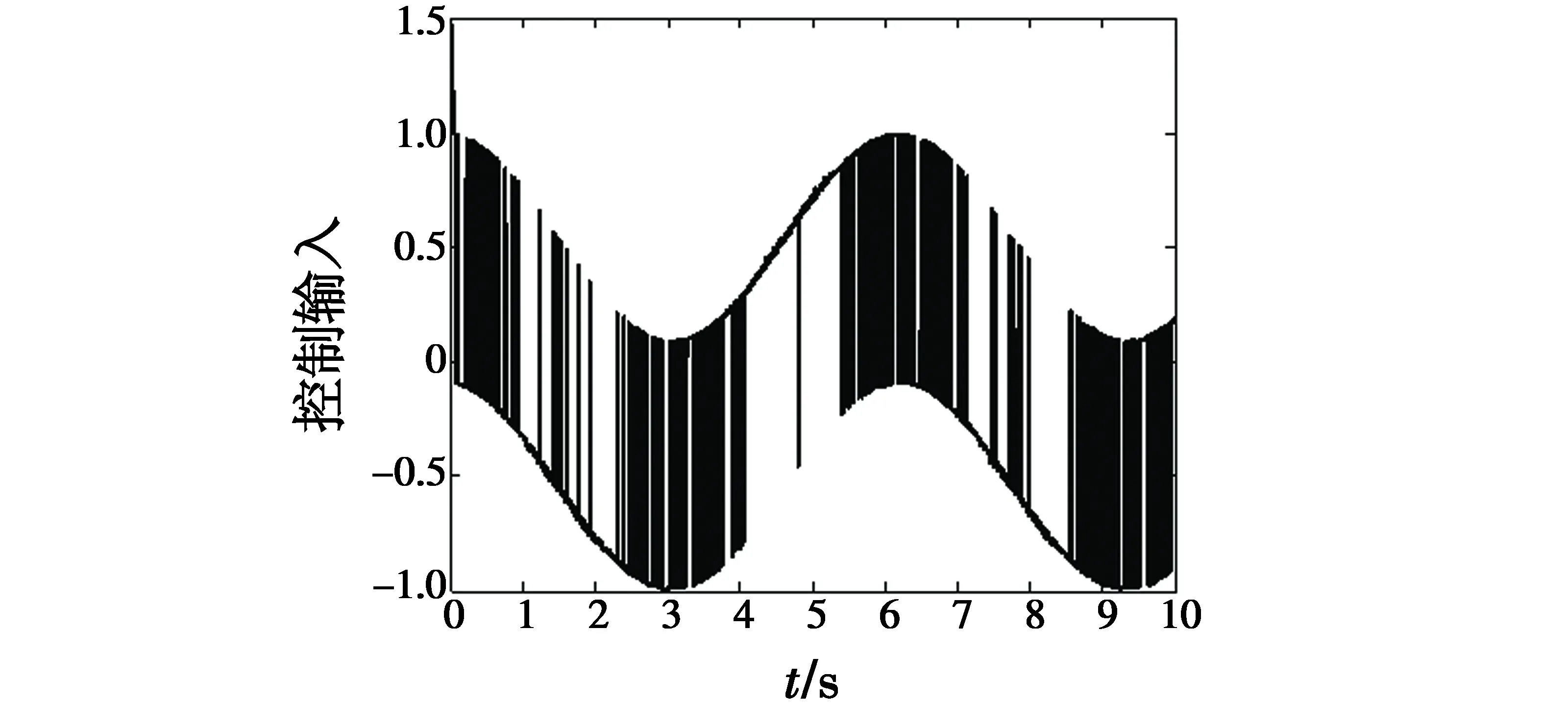
图3 控制输入u(SMVSC)Fig.3 Control input u(SMVSC)
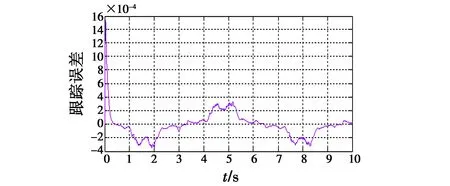
图4 角位置跟踪误差(SMVSC)Fig.4 Angular position tracking error(SMVSC)
由图2可知,系统对给定正弦信号能进行快速跟踪,角位置跟踪时间需要0.2 s,角速度跟踪时间需要0.3 s,但是由图3可知,电机存在较大的波动,这将会影响系统控制效果,导致系统不稳定。同时,由图4可知,系统的跟踪存在误差,反映在实际系统中则是电机振动,不利于视轴稳定。
2.2 基于神经网络滑模变结构控制器设计
陀螺稳定平台作为视轴稳定系统的一种常用结构,对系统的快速性和鲁棒性要求很高,而2.1节中的仿真实验表明,采用上述控制方法并不能有效地提高系统的鲁棒性。与此同时,在滑模控制中频繁地切换变结构控制方法会造成抖振,这将影响系统的控制效果[10]。
将滑模控制结合神经网络逼近用于非线性系统的控制,采用神经网络模型实现模型未知部分的自适应逼近,可以有效地降低误差增益。通过Lyapunov方法导出神经网络自适应律,通过网络权值的调节保证整个闭环系统的稳定性和收敛性。
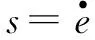
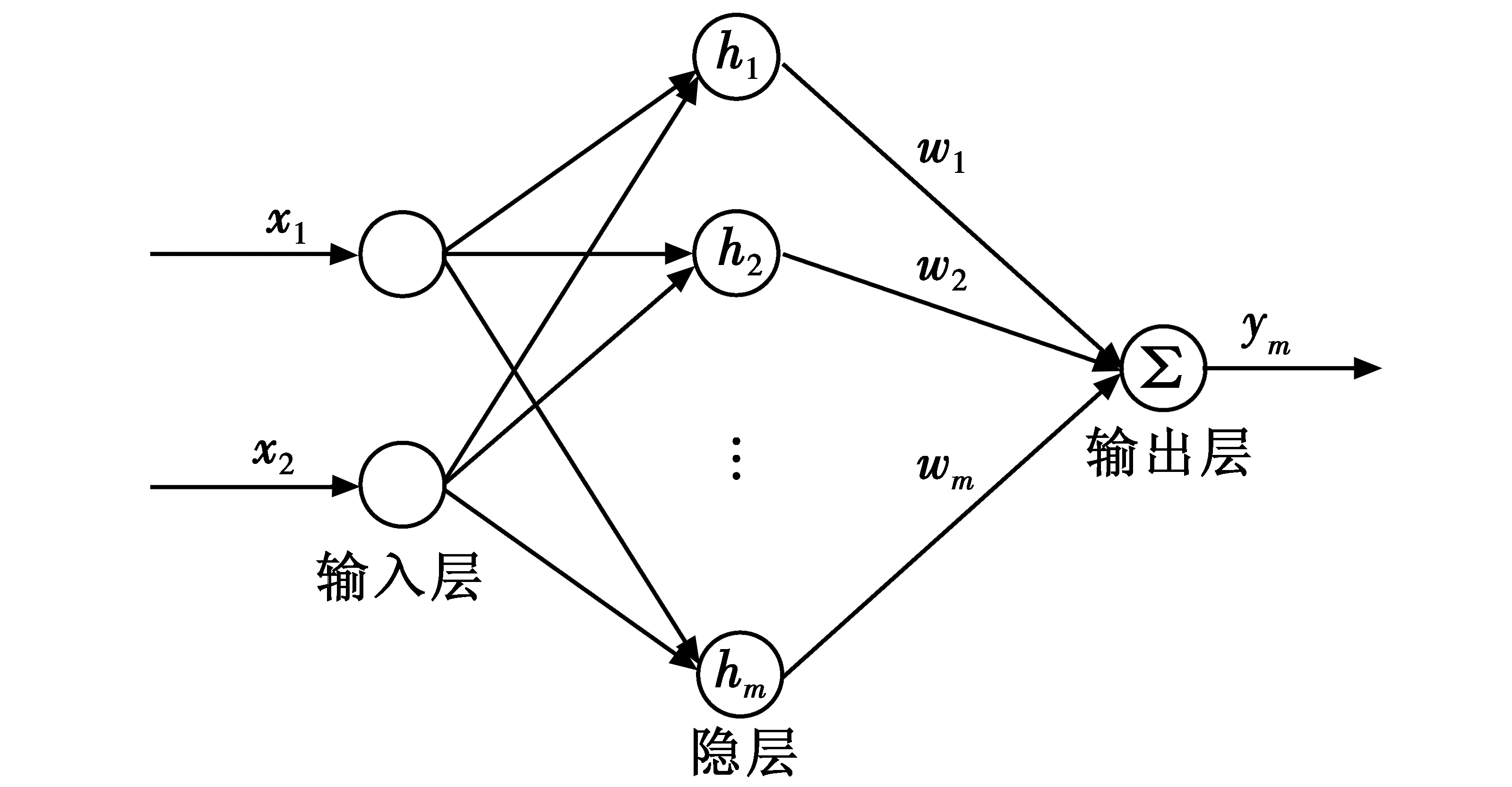
图5 RBF神经网络结构图Fig.5 RBF neural network structure
RBF输入输出算法为
(7)
式中:x为网络输入;cj为数据中心;bj为扩展常数;W*和V*分别为逼近f(·)和g(·)的理想网络权值;εf和εg为有界网络逼近误差。
根据滑模变结构的可达性设计控制律为
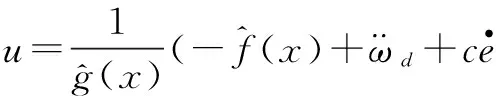
(8)
式中,η>0,μ>0,μs和ηsgns用来克服干扰和神经网络逼近误差,以保证系统稳定。
下面通过Lyapunov方法导出神经网络的自适应律。
设网络的实际输出为
(9)
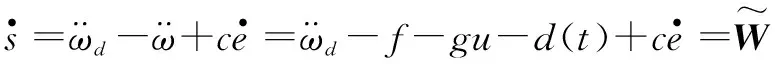
(10)
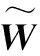
取Lyapunov函数为
(11)
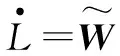
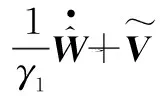
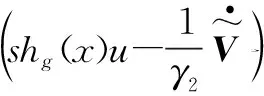
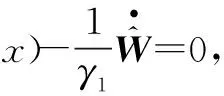
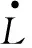
因此,可取自适应律为
(12)
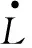
采用式(1)所示系统,系统参数取值见2.1节。采用神经网络滑模变结构控制器(NNSMVSC),控制器各参数取值为μ=10,γ1=10,γ2=1.0,c=10,η=0.001。
采用式(8)控制律和式(12)控制律,RBF网络的结构取2-5-1,取x1=ω,根据网络输入的实际范围来设计高斯基函数,取ci=[-0.1 -0.500.51.0]和bj=5.0权值的初始值为0.1,仿真结果如图6~图8所示。
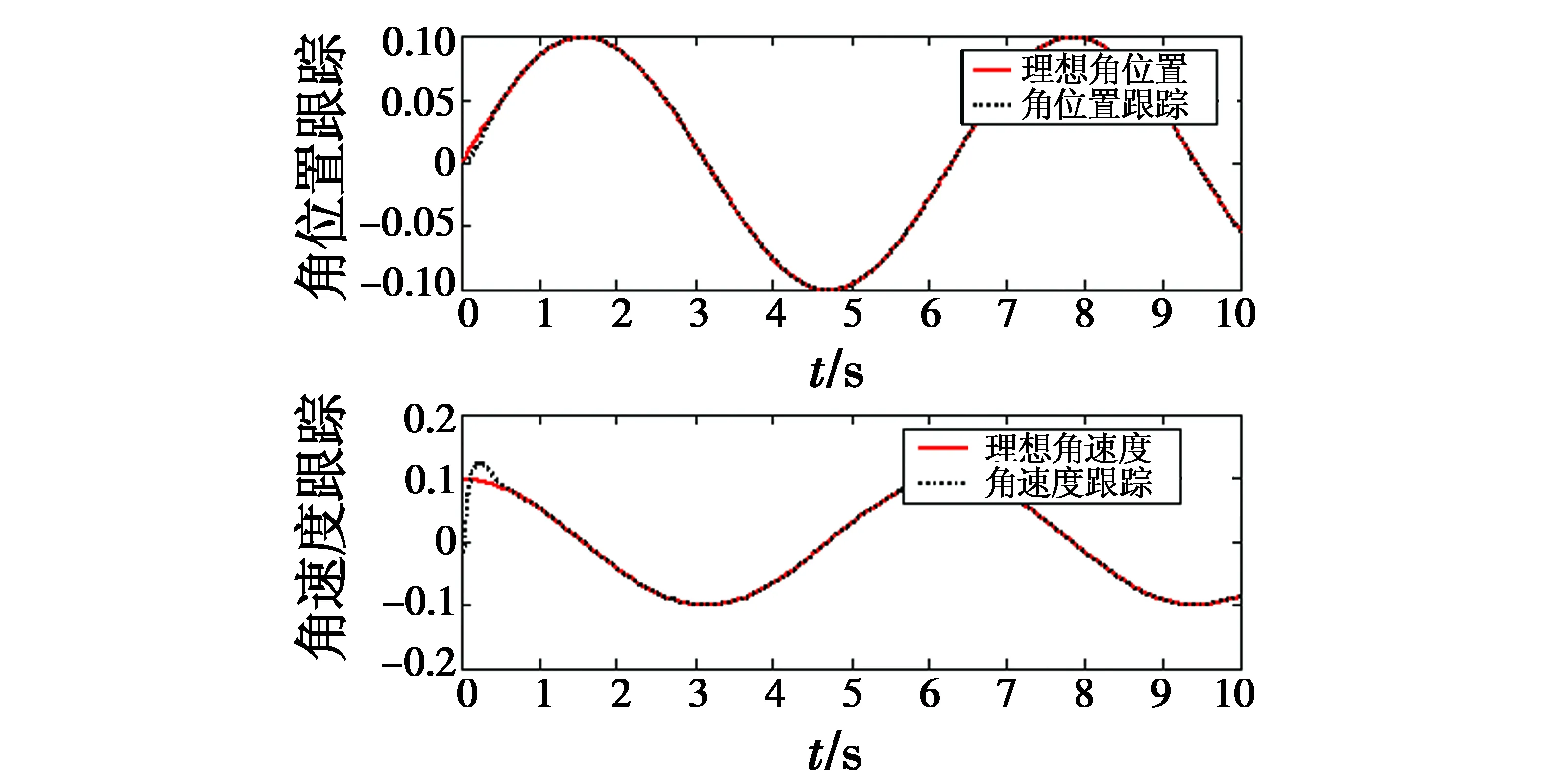
图6 角位置和角速度跟踪(NNSMVSC)
Fig.6 Tracking of angular position and angular velocity(NNSMVSC)
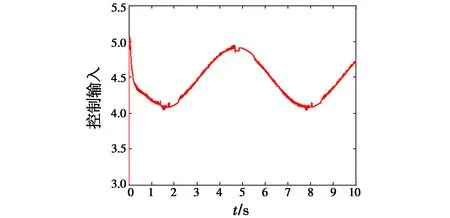
图7 控制输入u(NNSMVSC)Fig.7 Control input u(NNSMVSC)
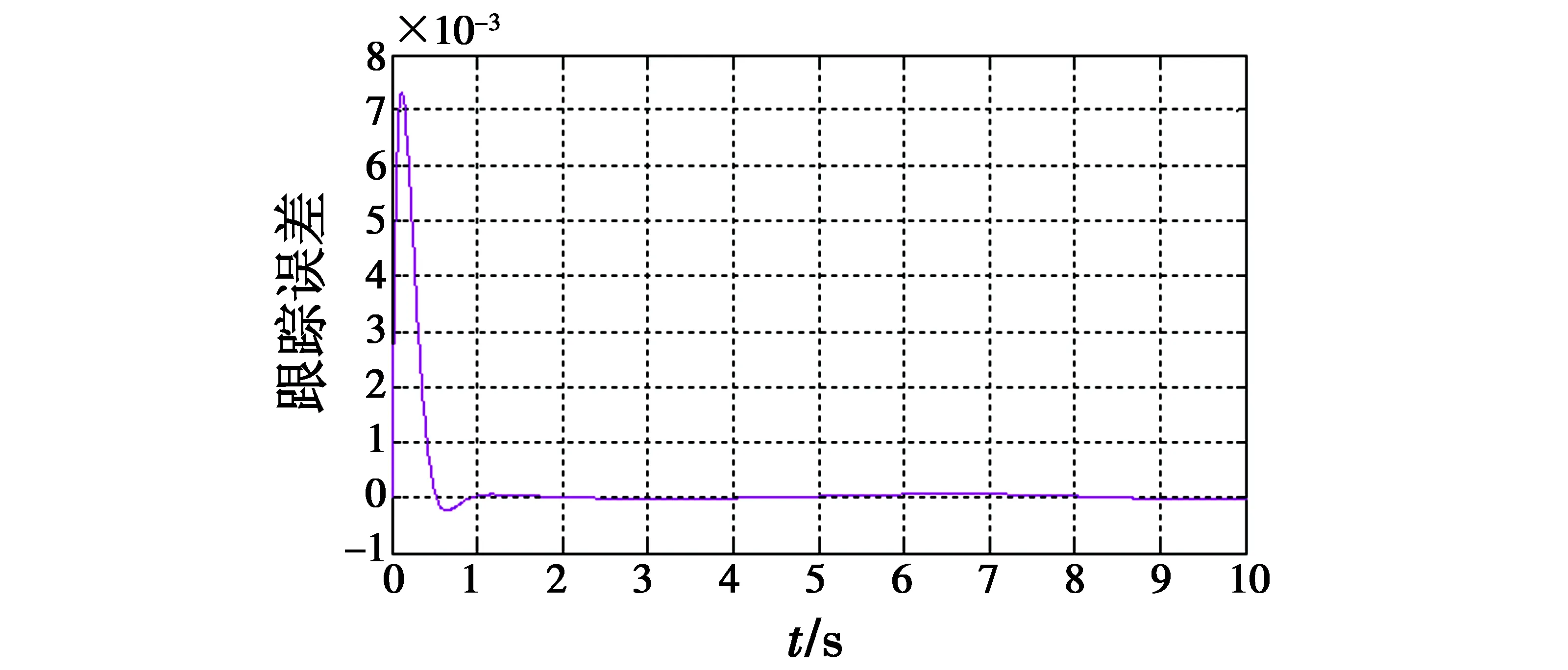
图8 角位置跟踪误差曲线(NNSMVSC)Fig.8 Angular position tracking error(NNSMVSC)
由图6可知,与采用指数趋近律的滑模变结构控制方法相比,基于神经网络的滑模变结构控制方法在跟踪时间上有一定的延长,在0.3 s时可实现对角位置的跟踪;在0.5 s时能够实现对角速度的跟踪。但是由图6可知,该方法对控制输入u有很大改善,同时由图8可知,采用该方法时,误差的最大值为0.007 3,且跟踪误差能在1 s时无限趋近于零。
但是当建模不确定项和干扰较大时,需要切换的增益项η较大,这会造成较大的抖动,因此可以考虑用饱和函数sat(s)代替符号函数sgns,即
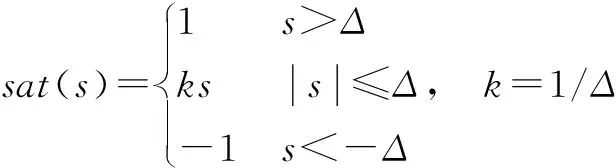
(13)
式中,Δ是边界层。由式(13)可知,在边界层外采用切换控制可使系统快速趋于滑动模态,在边界层以内采用反馈控制,以降低滑模切换控制产生的抖动。
采用上述系统,取k=0.001,利用改进的神经网络滑模变结构控制方法(INNSMVSC)仿真的结果如图9~图11所示。
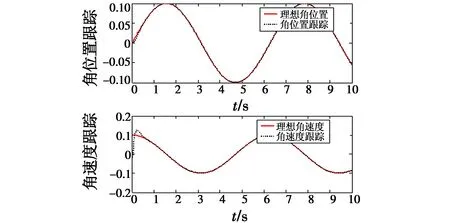
图9 角位置和角速度的跟踪(INNSMVSC)
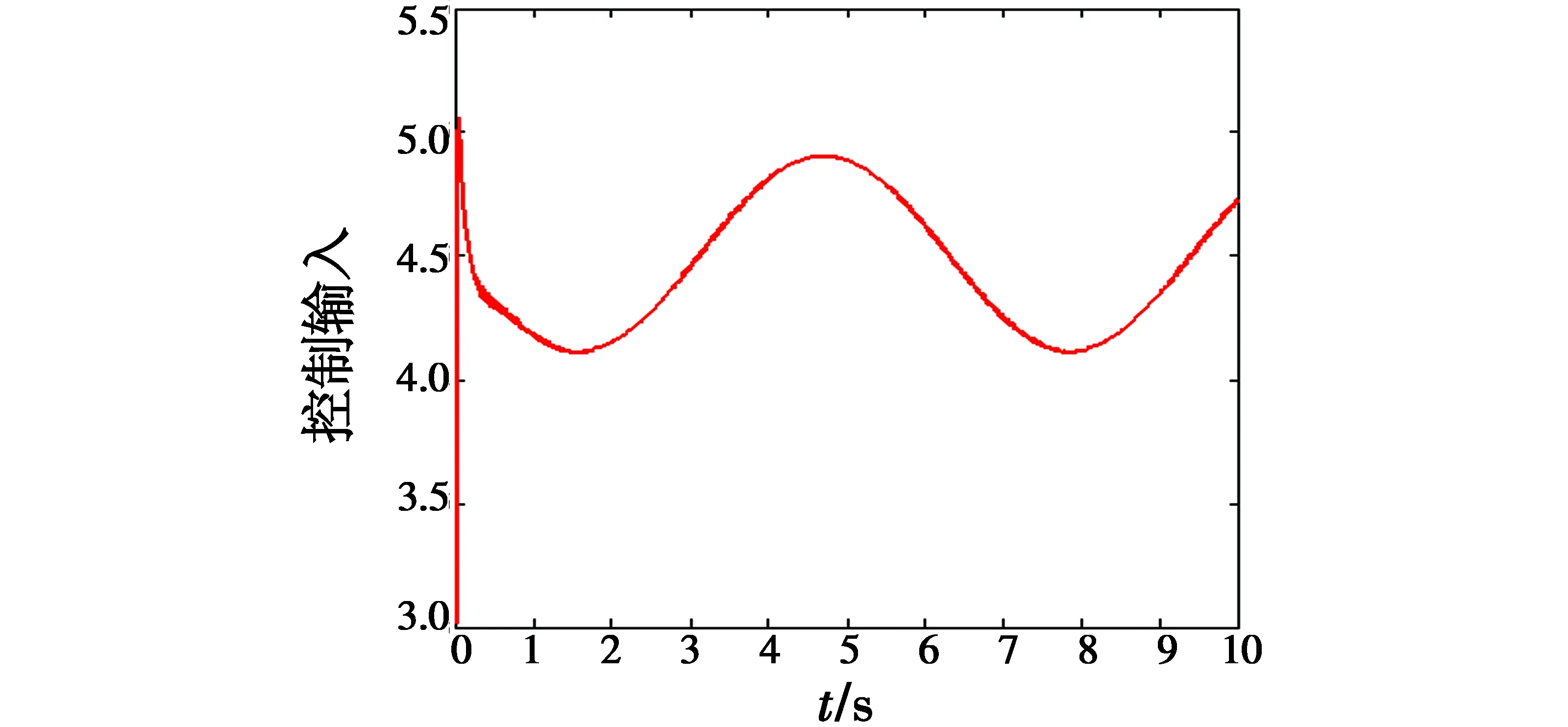
图10 控制输入u(INNSMVSC)Fig.10 Control input u(INNSMVSC)
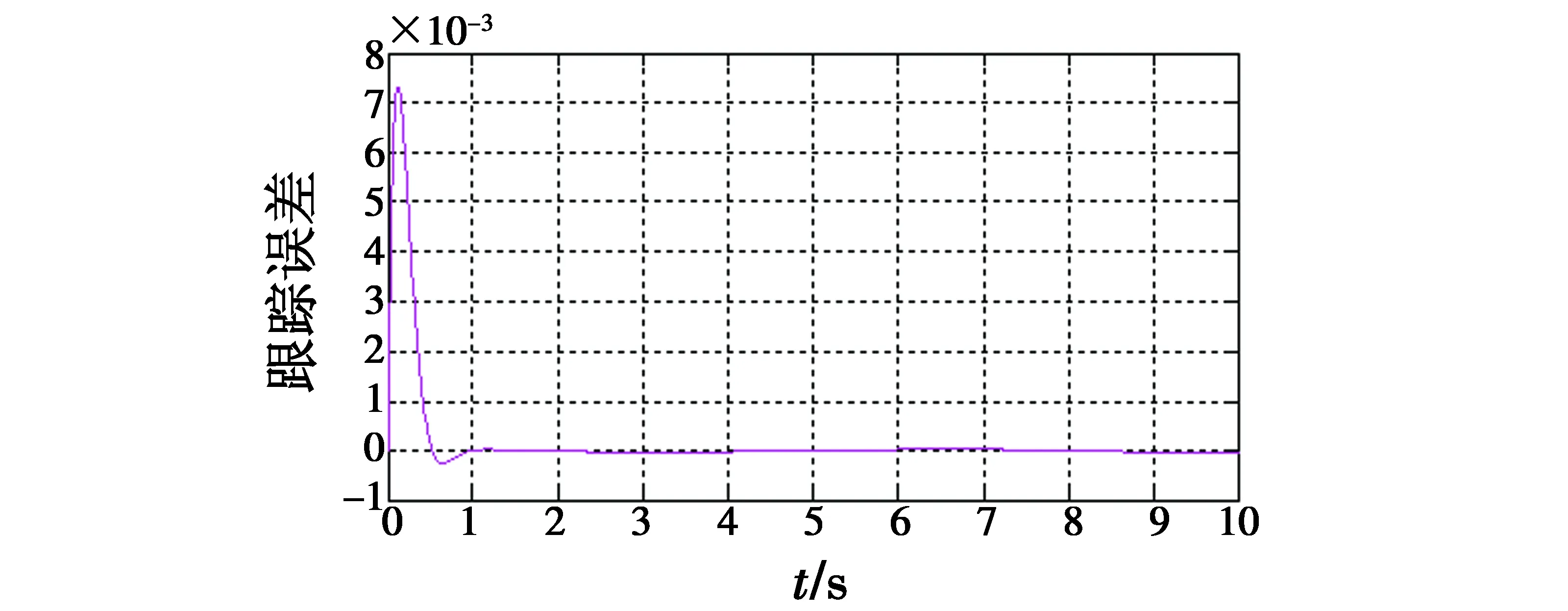
图11 角位置跟踪误差曲线(INNSMVSC)Fig.11 Angular position tracking error(INNSMVSC)
由图9可以看出,采用改进的神经网络滑模变结构控制方法,对系统角位置和角速度的跟踪无明显变化,但是由图10可知,采用该方法对控制输入有很大的改善。
由以上仿真实验结果可以看出,采用RBF神经网络滑模控制方法对陀螺稳定平台单轴系统进行控制时,仿真图2和图6证明,利用该方法能对陀螺稳定平台的角位置和角速度进行快速跟踪;图3和图7表明采用神经网络滑模变结构控制方法能对控制输入进行改善,这将进一步减少对系统的影响;图4和图8表明,采用神经网络滑模变结构控制方法对陀螺稳定平台进行控制,在误差允许范围内可无限趋近于0。
3 结论
陀螺稳定平台速度环的特性对整个平台的性能有很大影响。单独采用滑模变结构控制方法能对速度环的特性有一定的改善,但是外扰以及建模不确定性引起的抖动问题,使得系统的快速性和鲁棒性受到影响。由于RBF网络具有泛化能力较强、结构简单等优点,针对这个问题,提出采用RBF神经网络的优势弥补滑模变结构的缺陷。实验结果表明,在系统精确模型未知的情况下,该方法可以有效地提高速度环的性能;且神经网络滑模变结构控制器参数少、计算简单,可避免冗长的计算,具有较好的工程实现性。
