基于S函数的改进变步长LMS自适应算法
2018-10-13雷章勇彭志炜赵雪娇
雷章勇, 彭志炜, 张 俨, 赵雪娇
(贵州大学电气工程学院,贵阳 550025)
0 引言
在信号处理中,引入滤波器可在一定程度上削弱或消除噪声信号的影响。对于滤波器的应用,往往希望在实现滤波、平滑或者预测等任务的同时,实时跟踪和适应系统或环境的动态变化,这就需要滤波器的参数可以实时变化更新。自适应滤波器通常根据采样信号的变化不断更新滤波器的参数或者调整滤波器的结构,实现从含噪声信号中提取或者恢复有效的原始信号[1]。作为自适应滤波器设计的一个关键环节,自适应滤波算法常用的计算准则是使滤波器实际输出与期望输出响应之间的均方误差为最小,即最小均方误差准则(MMSE)。
由WIDROW提出的最小均方误差(LMS)算法是一种自适应算法,因算法简单、计算量小、鲁棒性强、易于实现的特点[2-3],被广泛应用于通信、系统辨识、回波消除和自适应谱线增强等领域[4-5]。该算法基于MMSE准则,通过步长因子的选择实现对权值的更新,以获得最优权值。在这个过程中对步长因子的取值影响算法各方面的性能,包括收敛速度、稳态误差、对时变系统的跟踪能力以及抗噪声干扰能力等[6-8]。根据对步长因子构造方式的不同,LMS算法主要分为传统定步长LMS算法和变步长LMS算法。
传统定步长LMS算法将步长因子取为固定值进行权值更新。在此过程中,如果对步长因子取值不当将会使算法的性能受到影响。若步长因子取值较大,在初始阶段,算法的收敛速度较快,但会在接近稳态时产生较大的稳态误差;反之,若步长因子取值较小,算法在收敛时稳态误差也较小,但会降低算法的收敛速度[9-11]。可见,传统定步长LMS算法中步长因子的取值难以同时满足算法对收敛速度与稳态误差两个性能指标的要求,因此许多文献[12-15]提出了变步长LMS算法。通过建立误差与步长因子之间的非线性函数关系进行权值更新,该方法可兼顾收敛速度与稳态误差,有效弥补定步长LMS算法的不足。文献[12]提出一种新的变步长自适应滤波(SVSLMS)算法,可获取较快的收敛速度和跟踪速度,但由于在收敛阶段步长的变化较快,从而造成稳态误差较大。针对文献[12]算法的不足,文献[13]提出一种新的变步长自适应滤波算法,该算法给出了新的步长因子调整函数,使得步长在误差接近零处具有缓慢变化的特性,减小了稳态误差。文献[14]提出的变步长LMS滤波算法克服了S函数变步长LMS算法稳态阶段步长变化较大的缺陷,该算法在初始阶段或系统发生时变阶段具有较大的步长,且稳态时步长较小。文献[15]提出一种新的基于箕舌线的变步长LMS算法,该算法对步长因子的计算较为简单,同时算法滤波效果好。
通过对上述文献进行分析可以看出,改进变步长LMS算法对步长因子的调整原则都是要求在初始阶段或系统发生时变后,步长能够取得较大值,使得算法具备较快的收敛速度或对时变状态下信号的快速跟踪;而在收敛阶段则要求步长变化较慢且取值较小,以减小稳态误差和避免稳态失调。根据上述现有算法理论,为进一步改善变步长LMS自适应滤波算法的性能,本文基于S函数曲线特点提出一种新的改进变步长LMS自适应滤波算法,该算法能够兼顾收敛速度和稳态误差,且具有一定的抗干扰能力。
1 LMS自适应滤波算法
自适应滤波算法原理如图1所示。其中,x(n)和y(n)为输入信号和输出信号,v(n)为噪声信号,d(n)为期望输出信号,e(n)为误差估计信号。该算法最广泛使用的算法形式为下降算法,实现方式主要有自适应梯度算法和自适应高斯-牛顿算法。
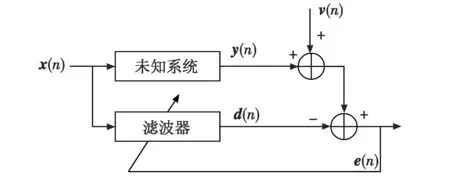
图1 自适应滤波算法原理图Fig.1 Schematic of the adaptive filtering algorithm
LMS自适应滤波算法属于自适应梯度算法,该算法根据权值的梯度估计值搜索出最优权值,计算出滤波器输出信号与期望信号之间的误差,并以误差方差最小作为判据修改权值系数。算法迭代算式为
e(n)=d(n)-xT(n)W(n)
(1)
W(n+1)=W(n)+ue(n)x(n)
(2)
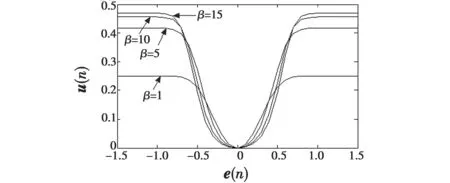
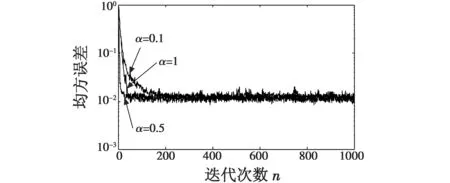
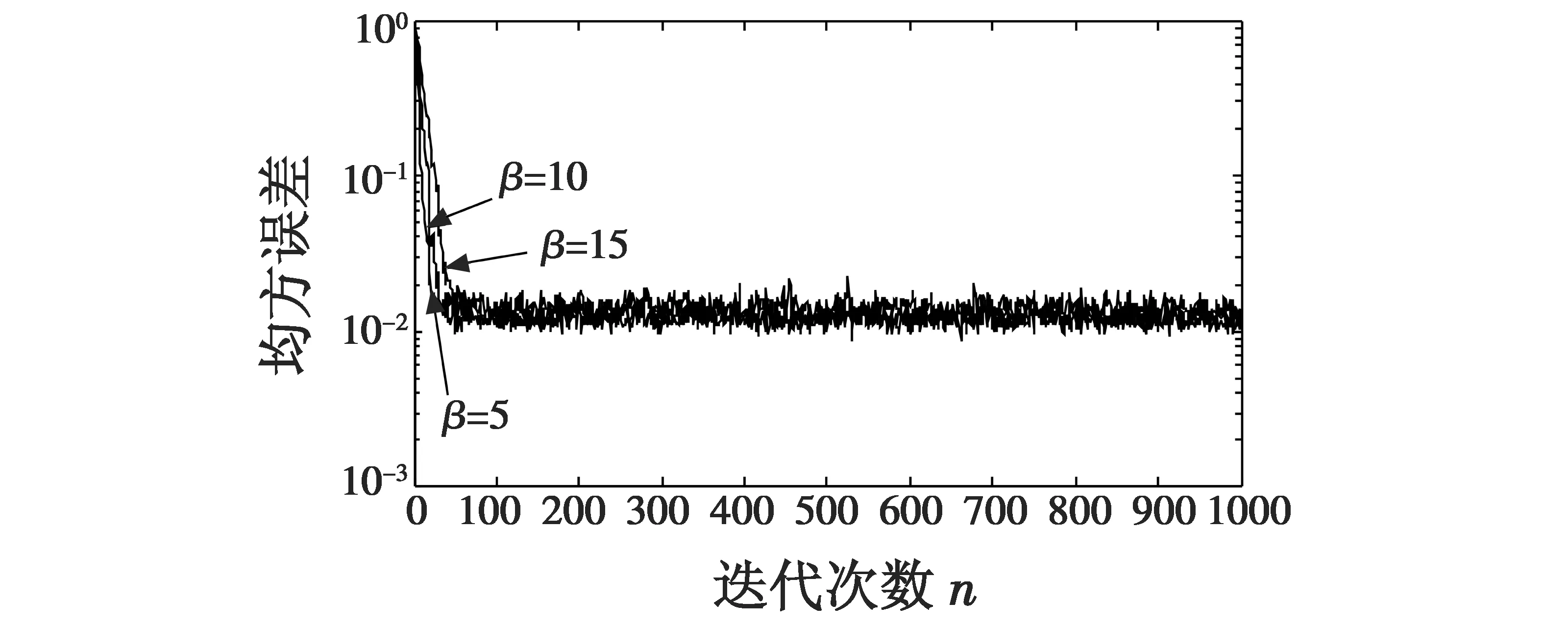
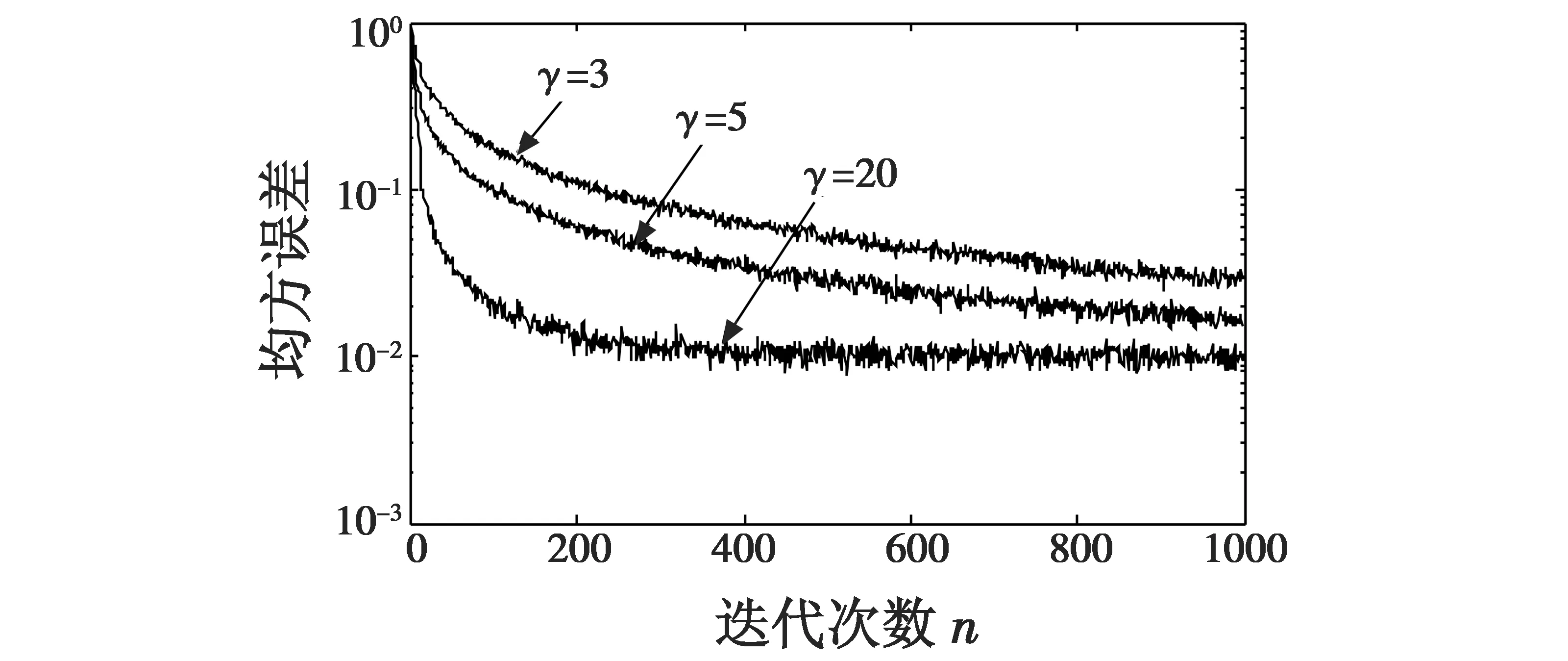
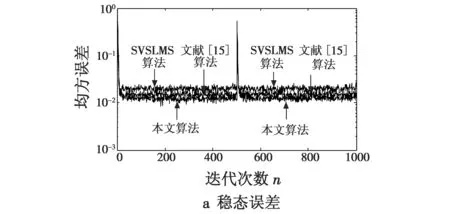
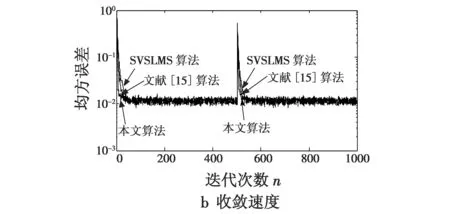
式中:W(n)为滤波器在n时刻的权值向量;u为步长因子,其取值将影响算法的收敛性和稳定性,使算法收敛的步长因子u的取值需满足条件0 根据变步长LMS自适应滤波算法对步长因子调整的特点,结合S函数(如式(3))及其曲线(如图2)来构造算法的步长因子模型。 (3) 图2 改进LMS算法步长因子表达式的构造过程Fig.2 The construction process of the step-size factor for improved LMS algorithm 首先将S函数表达式分母的指数项乘以系数β(β>0),实现函数曲线水平方向上的第一次平移,再把平移后的曲线在竖直方向向下平移Δ=1/(1+β)个单位,然后对函数取绝对值得到变换后的曲线,如图2所示,该曲线对应的u(n)与e(n)的函数关系为 (4) 根据S函数变换后得到的曲线分析可知:当误差值较大时,对应的步长因子可以取得较大值;而当误差值 减小到-5 为了提高算法的可控性,在表达式(4)中引入参数α,γ和m,得到步长因子u(n)与误差e(n)之间的非线性函数关系式为 (5) 下面分析步长因子表达式中的4个参数对步长因子调整的影响。 1) 参数m的分析。 分别取α=0.1,β=10,γ=10,得到m为1,2,3时e(n)与u(n)的曲线,如图3所示。 图3 m变化时的步长因子曲线Fig.3 The step-size factor curve when m changes 可以看出,当误差值接近零时,m取值越大,步长因子变化就越趋于平缓;当误差值为0时,步长因子取值也变为0。而在LMS算法中,收敛阶段步长变化的快慢对稳态误差和稳态失调量有较大的影响,步长因子变化快容易引发振荡现象。从图中还可看出,m取值越大,步长因子在误差接近0的过程中变化速度越慢,对稳态误差和稳态失调量的调整就越好。但另一方面,若m取值过大,将出现误差取值较大时步长因子就开始减小的现象,例如当误差值约为0.5时,m=3对应的曲线已经下降到步长因子幅值约为0.02处,而m=1对应的步长因子幅值仍约为0.09。这样,m取值过大,将会降低算法的收敛速度。此外,m取值过大将使得计算量增大,增加算法处理数据的时间。因此,本文算法对步长因子中参数m的取值为2,进一步得到的u(n)与e(n)的函数关系为 (6) 2) 参数α的分析。 分别取β=10,γ=10,m=2,得到α为0.1,0.3,0.5时e(n)与u(n)的曲线,如图4所示。可以看出,参数α的取值对u(n)幅值的影响较大。α取值越大,u(n)的幅值越大,算法的收敛速度就越快。其中,u(n)的 最大极限值为u(n)max=a[1-1/(1+β)],这里也可以看出,当α取定值,β越大,对应的u(n)max越大。但α的取值不能无限大,需满足LMS自适应算法收敛对u(n)的取值要求。 图4 α变化时的步长因子曲线Fig.4 The step-size factor curve when α changes 3) 参数β的分析。 分别取α=0.5,γ=10,m=2,得到β为1,5,10,15时e(n)与u(n)的曲线,如图5所示,相应的u(n)最大值u(n)max如表1所示。根据图5可以看出,β取值越大,u(n)在误差值接近0附近的变化趋势越平缓。又由表1可知,当β≥5时,随着β取值逐渐增大,u(n)max受到的影响逐渐减小。但若β取值较大,会出现在误差值还较大时u(n)就开始减小的现象,将会降低算法的收敛速度。 图5 β变化时的步长因子曲线Fig.5 The step-size factor curve when β changes 表1 不同β取值对应的u(n)max 4) 参数γ的分析。 分别取α=0.5,β=10,m=2,得到γ为5,10,15时e(n)与u(n)的曲线,如图6所示。可以看出,γ=5时对应的曲线在误差取值逐渐接近0时,u(n)的变化速度最慢,而其对应的曲线在误差取值约为1.3时,幅值就开始减小,而另外两条曲线在误差分别为0.6和0.8时曲线幅值才出现减小的趋势。可见,γ取值越小,在误差取值逐渐接近0时,u(n)变化速度越慢,有利于减小算法的稳态误差;但γ取值较小,不能满足在误差较大时u(n)也要求取得较大值的调整原则。 图6 γ变化时的步长因子曲线Fig.6 The step-size factor curve when γ changes 通过上述各参数变化对步长因子影响的曲线及分析得出,固定参数m=2后,参数α变化主要影响u(n)的幅值调整,可用于控制算法的收敛速度,且可控性较好;参数γ的变化主要影响u(n)在接近稳态时的幅值变化速度,用于调整算法的稳态误差。参数β取值可同时影响收敛速度和稳态误差,但当β取较大值时,参数β对u(n)幅值的影响较小,因此其作用主要是稳态误差的微调。 在实际中,外界对系统的干扰具有随机性和任意性的特点。因此,为了增强算法的抗干扰能力,在步长因子模型中引入误差向量自相关值e(n)e(n-1)来调节步长因子取值。经过整理,最后得到本文提出的基于S函数的改进变步长LMS自适应滤波算法的流程如下。 e(n)=d(n)-xT(n)W(n) (7) (8) W(n+1)=W(n)+u(n)e(n)x(n)。 (9) 本文提出的算法通过在步长因子模型中引入误差向量自相关值来增强算法的抗干扰能力,下面分析该量的引入对外界扰动的抑制机理。 由式(7)有 d(n)=xT(n)W(n)+e(n) (10) 根据自适应原理有 d(n)=xT(n)W*(n)+v(n) (11) 式中:噪声信号v(n)与输入信号x(n)不相关;W*(n)为自适应滤波器的最优权系数。假设权系数偏差为ΔW(n),则 ΔW(n)=W(n)-W*(n) (12) 由式(7)~式(12)有 e(n)e(n-1)=v(n)v(n-1)-ΔWT(n)x(n)v(n-1)- v(n)ΔWT(n-1)x(n-1)+ ΔWT(n)x(n)xT(n-1)ΔW(n-1) (13) 由于v(n)均值为零,且与x(n)不相关,故有 E[e(n)e(n-1)]=E[ΔWT(n)x(n)xT(n-1)ΔW(n-1)] (14) E[e2(n)]=E[v2(n)]+E[ΔWT(n)x(n)xT(n)ΔW(n)] (15) 通过式(14)与式(15)的对比容易看出,利用式(8)调整LMS算法的步长,在强干扰信号下,算法性能受干扰信号v(n)的影响较小,并且在收敛阶段权系数偏差ΔW(n)较小。可见,误差向量的引入可增强算法的抗干扰能力。 根据本文算法,通过仿真得出步长因子模型中参数α,β和γ取不同值对滤波性能的影响学习曲线,如图7~图9所示。仿真条件:输入信号为以+1,-1等概率交替的信号,并叠加与输入信号不相关、均值为0、方差为0.01的高斯白噪声信号,滤波器阶数为2,采样点数为1000,分别做400次独立仿真。 图7 α变化时的算法收敛曲线Fig.7 Convergence curve of the algorithm when α changes 图8 β变化时的算法收敛曲线Fig.8 Convergence curve of the algorithm when β changes 图9 γ变化时的算法收敛曲线Fig.9 Convergence curve of the algorithm when γ changes 图7的仿真结果表明,α=0.5时算法的收敛速度最快,即在步长因子所含参数中,当β,γ和m取固定值时,并不是α越大算法性能越优。图8中,β为5对应算法的收敛速度较快,但收敛后的稳态误差较大;这是因为误差值较大时,β分别为10,15对应的步长因子幅值下降速度比β为5时对应幅值下降速度快,并且在稳态时β分别为10,15的曲线斜率较小,步长因子幅值变化速度较慢。由图9可以看出,γ取值较大时对应的算法收敛速度快,且稳态误差较小,但根据上节γ对步长因子的影响分析可知,γ取值不宜过大。 综上,本文提出的基于S函数的改进变步长LMS算法中步长因子所含参数值的求取可通过多次实验来获得,以实现算法性能最优。 采用上文参数对滤波性能的影响分析中的仿真条件,并假设在迭代次数n=500时系统发生时变,权系数变为w=[0.4,0.2],得到SVSLMS算法、文献[15]算法和本文算法对应的学习曲线如图10所示。 图10 本文算法与其他算法的比较Fig.10 Comparison between the proposed algorithm and other algorithms 由图10a可以看出,在收敛速度相同的情况下,本文算法稳态误差更小。图10b中,在相同误差条件下,本文算法具有较快的收敛速度。此外,在系统发生时变后,本文算法能够对信号进行快速跟踪,且收敛速度最快,说明算法具备一定的抗干扰能力。综上,本文算法与SVSLMS算法和文献[15]算法相比性能更优。 本文对现有变步长LMS自适应滤波算法进行研究,根据算法中步长因子的调整原则以及S函数曲线的特点,提出一种基于S函数的改进变步长LMS自适应算法,并分析了步长因子中各参数的取值对算法性能的影 响。与现有算法进行的仿真对比表明,本文所提改进算法在满足快速收敛的同时,收敛后的稳态误差也较小,且抗干扰能力较强,改善了现有算法的性能。2 改进LMS自适应滤波算法
2.1 机理分析
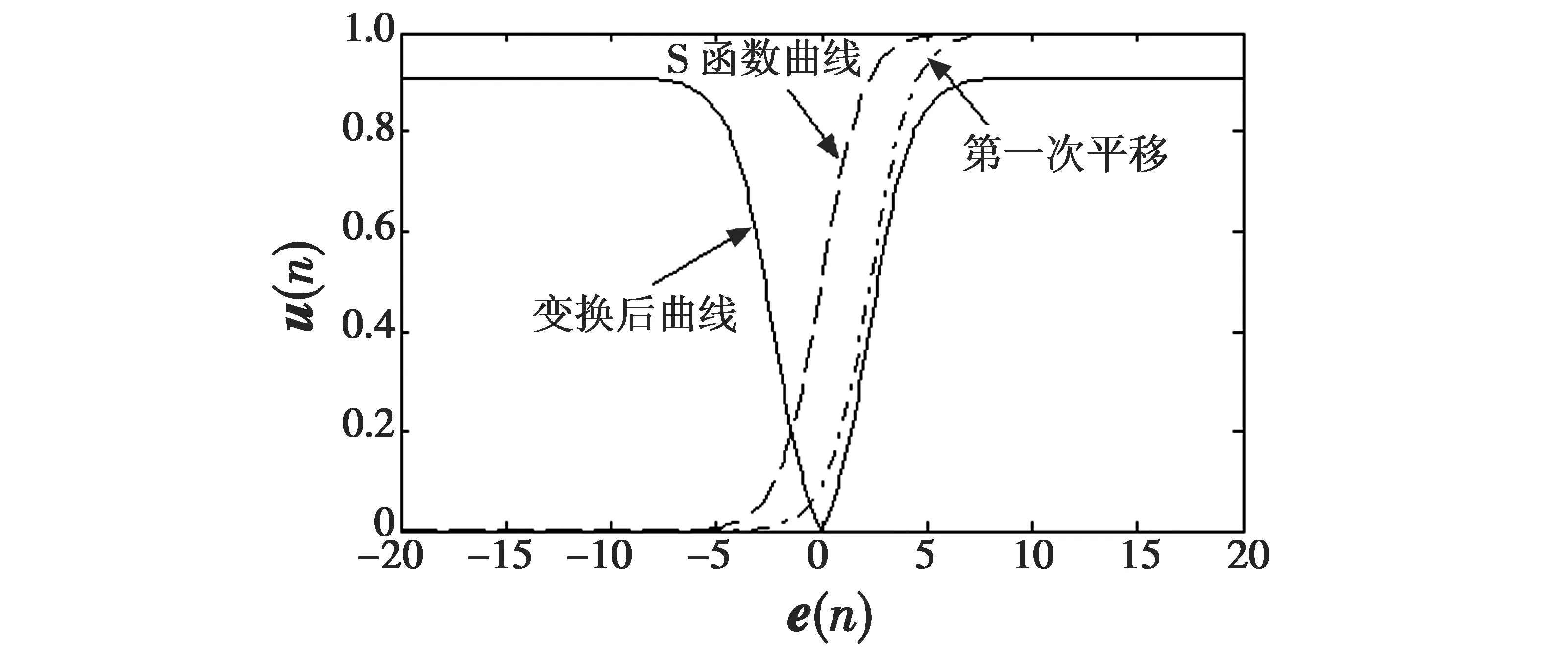
2.2 参数对u(n)的影响分析
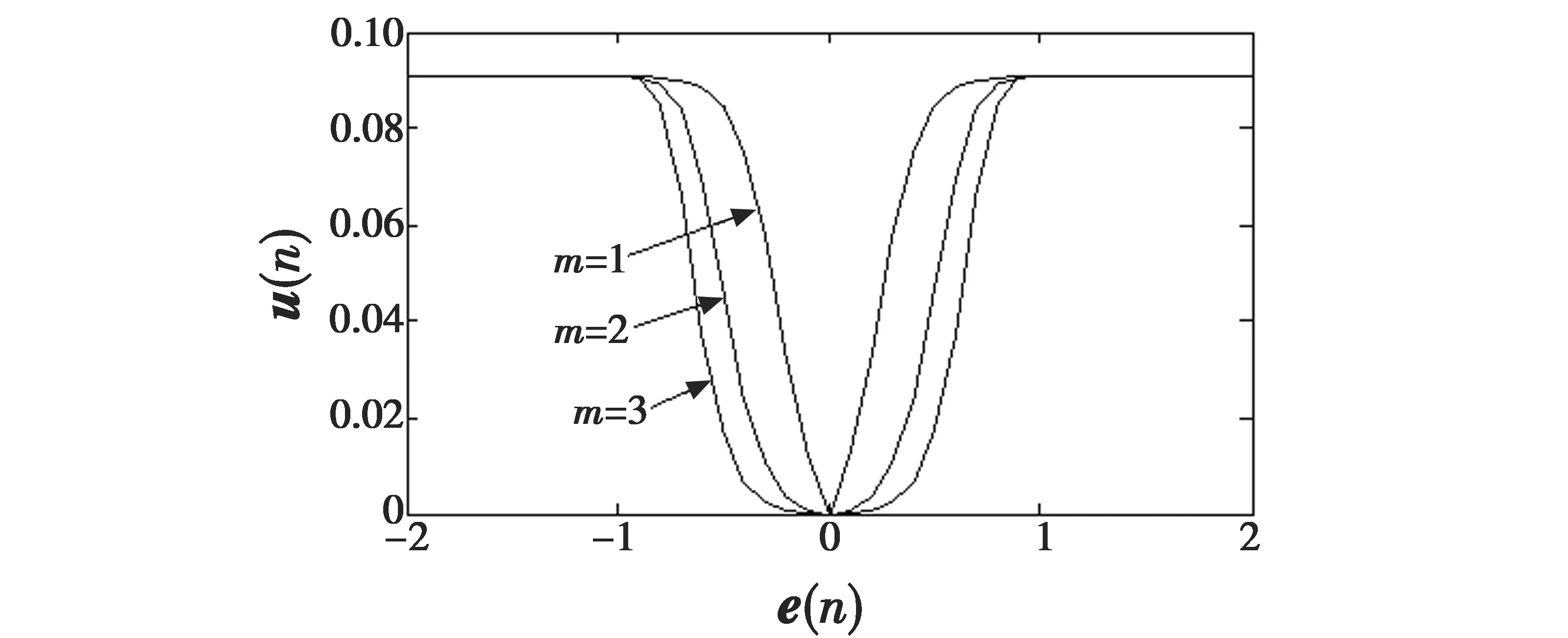
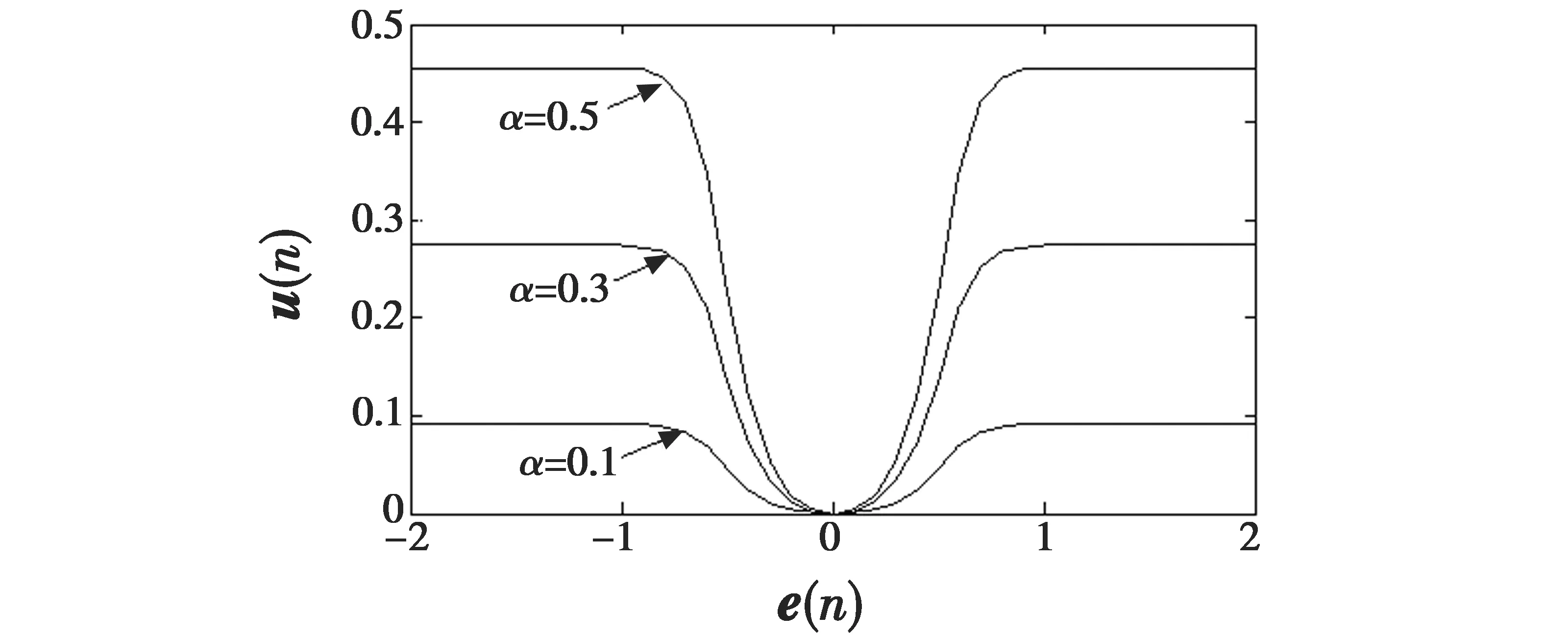


2.3 算法抗干扰性分析
2.4 参数对滤波性能的影响分析
3 仿真对比与分析
4 结束语
