卫星导航定位P码直接捕获算法研究

2018-10-13曾芳玲

电光与控制 2018年10期

徐浩, 曾芳玲

(国防科技大学电子对抗学院，合肥 230037)

0 引言

全球定位系统简称GPS，提供的定位服务分为两种，分别是由C/A码调制的信号提供的标准定位服务(SPS)，以及由P码调制的信号提供的高精度定位服务(PPS)[1]。无论是通过C/A码还是通过P码进行定位等服务，首先必不可少的环节便是完成对码的捕获。C/A码捕获相对简单，而P码因为周期长，捕获较为困难，捕获的时间也比较长，难以满足实时性的要求。所以GPS接收机P码捕获技术的研究成为一直以来的研究重点，目前也取得了一定的研究成果。

传统的P码捕获方法，一般是通过首先捕获C/A码，然后根据接收到的C/A码中包含的有效信息，进行P码的捕获[2]。但是由于C/A码容易受到外来干扰，一旦被干扰便无法再进行P码的捕获，因此研究P码的直接捕获技术在GPS应用特别是军事应用中是十分迫切的。目前，P码的直接捕获方法主要包括时域方法和频域方法。时域捕获方法包括不借助C/A码而进行P码直接并行多通道捕获的方法，虽然不会受C/A码干扰的影响，但捕获时间较长，捕获速度很慢，难以满足实时性的要求，并且时域相关要进行大量的相关运算，需要相当多的硬件资源。

因此，从捕获速度、资源利用等方面综合考虑，P码的直接捕获方法研究主要集中在频域。目前频域的方法主要包括基于FFT的循环相关捕获法、扩展复制重叠法(XFAST)、均值法等方法[3]。频域捕获方法基本上均以FFT为基础，从根本上讲都是基于FFT捕获算法的优化。

本文以上述均值捕获方法和XFAST方法为基础，提出一种时频融合的捕获算法，其基本思想是对本地序列进行扩展复制重叠处理，在不影响相关度的基础上扩大搜索范围，并对处理后的本地序列和接收序列进行均值处理，以提高捕获速度，同时在时域上对载波多普勒频移进行并行搜索。另外，对这种方法进行了进一步的优化，并通过仿真分析证实优化后的方法在捕获时间上有了一定进步。

1 P码频域捕获算法原理

P码的码周期很长，相关捕获的时间也比较长，难以满足实时性的要求[4]。所以P码的快速直接捕获方法主要集中在频域，主要是采用频域相乘代替时域的相关运算，减少了运算量，提高了捕获速度。其主要的原理是基于信号的互相关、线性卷积以及循环卷积之间的关系[5]。对于两个信号x(n)和h(n)，它们之间的信号相关和信号FFT之间存在如下的关系

(1)

根据上述关系，现只需要进行2次FFT和一次IFFT运算，就能得到与信号相关同样的结果，明显地减少了运算量、缩短了运算时间。虽然采用FFT捕获P码相对于频域相关捕获来说减少了运算量，提高了捕获的速度，但是P码的长周期使得直接采用FFT捕获用时依然较长，因此在FFT的基础上进行一些处理，来进一步提高捕获速度。

1.1 扩展复制重叠捕获算法

扩展复制重叠捕获算法以FFT变换为基础[6]，其主要思想是将本地伪码分成M段，每一段的长度包含L个码元，然后将这M段子码段对应位置进行算术相加，得到1个新的重叠的码段，这个码段的长度为L,但包含了原来长为M×L的码段的信息。图1以M=4，L=4对主要原理进行了解释。

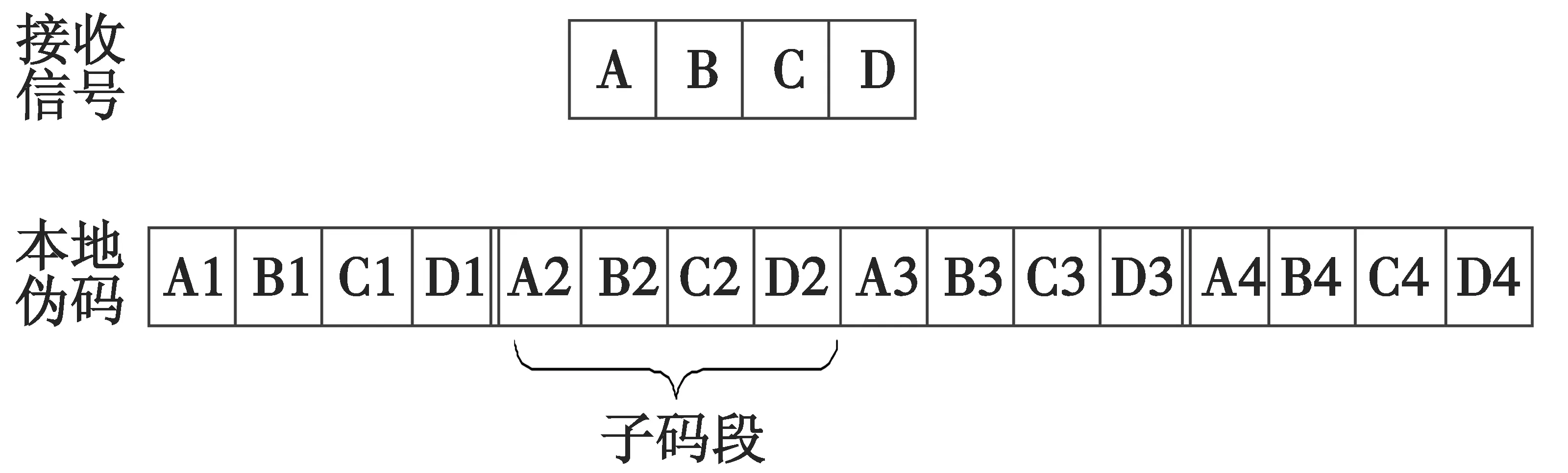
图1 扩展复制原理Fig.1 Extended replication principle

根据上述原理，将本地P码分成M段，每段对应位置相加得到新的重叠码段，然后根据频域捕获原理进行循环相关，找到这个新的重叠码和接收码的最大相关结果G1。若相关结果大于门限值，便得到了接收码在本地重叠伪码中相对于段首的相对位置m，但此时并不确定是在哪段子码段中。再将接收信号和每段子码段在相对m的位置分别进行频域相关运算，得到m个相关结果，找出最大相关峰值G2出现在哪个子码段中，记为d，那么伪码偏移的位置为(d-1)L+m。

扩展复制重叠减少了FFT的点数和运算量，相对于直接FFT方法，捕获时间增加了很多。但是由于子码段之间的叠加，增加了背景噪声，而且可能产生峰值的多值性，因此，重叠子段数不能无限制增加。表1给出了该算法的仿真测试结果，其中，接收信号的参数：信噪比为-12 dB，中频频率为20.46 MHz，l(l=2L)为每次FFT的点数,M为扩展段数。G1和G2分别表示上述过程的两个相关峰值，不同之处在于采用的是最高峰值和平均峰值比例，以便于直观地表示峰值的分辨能力；T1和T2分别表示1次搜索到和无峰值条件下搜索1 000 000码片所用时间。

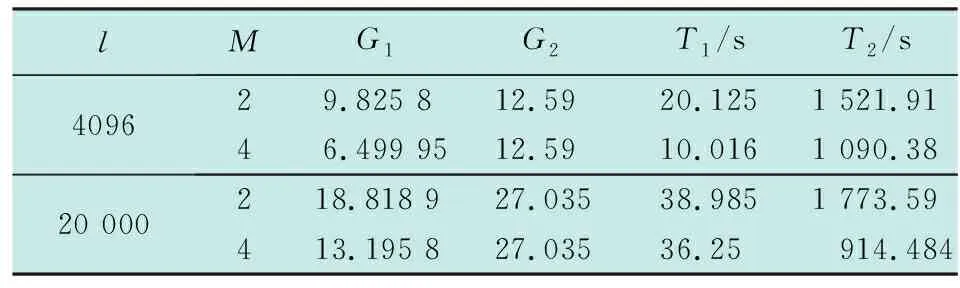
表1 XFAST捕获算法处理结果

统计分析表明，M值越大，峰值不存在的情况下搜索时间相对越短，但峰值也越模糊，码片误差越大，捕获越不准确，因此XFAST在提高捕获速度上能力也是有限的。

1.2 均值捕获算法

均值捕获算法以循环相关理论为基础，它不仅使用循环相关的方法使搜索时间的覆盖域扩大，而且通过分段补零的方法很好地实现了频域的码多普勒频移的补偿[7]。其原理如图2所示。

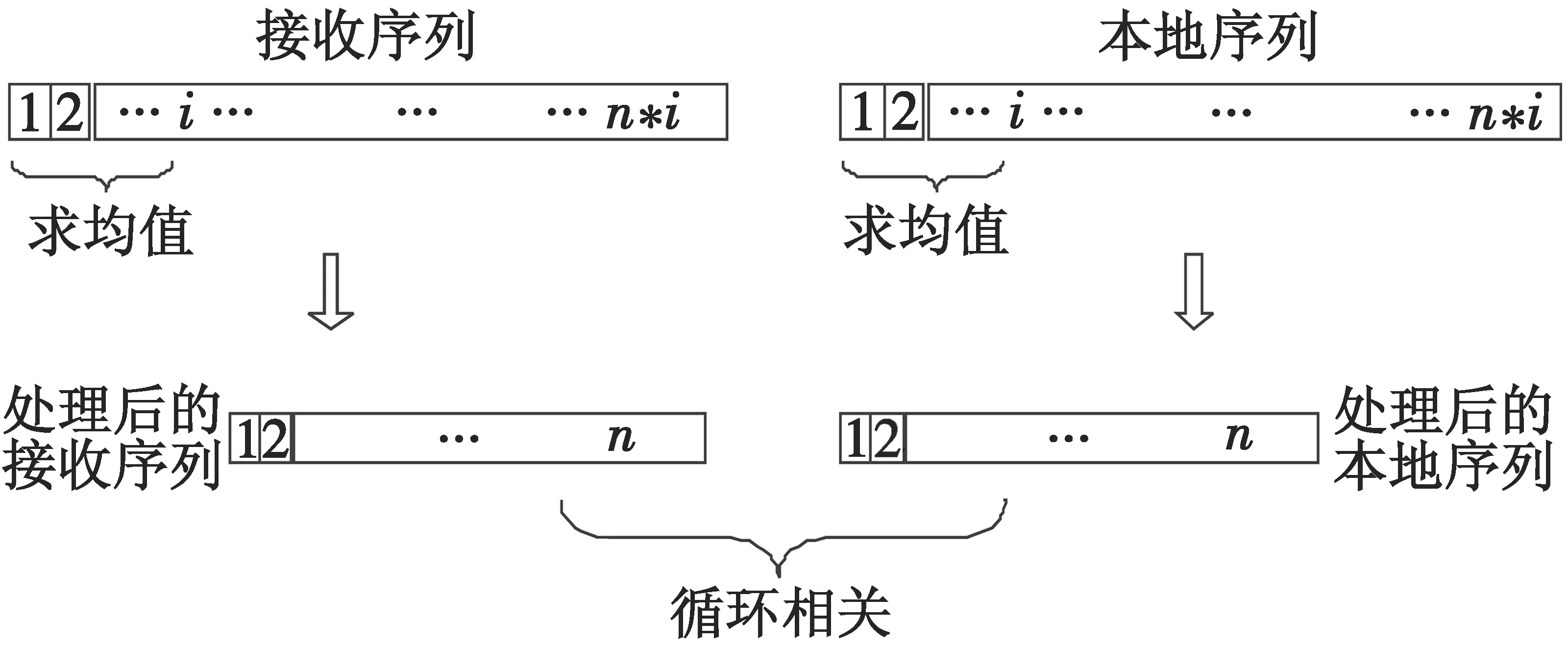
图2 均值算法原理Fig.2 Principle of the mean algorithm

均值算法减少了FFT运算的点数，提高了处理的速度，但是平均的码段越长，其码相位偏移越大，峰值捕获的性能越差，因此平均的码段长度不能过长，这就在时间域上限制了检索范围。表2给出了相同仿真参数下的分析结果，其中，i为均值的点数，G1，G2，T1和T2表示的意义与表1相同。

表2 均值捕获算法处理结果

经统计分析,i值越大，单次运行时间越长，峰值不存在的情况下搜索时间相对越短，但峰值也越模糊，码片误差越大，捕获越不准确。因此均值点数受到限制，捕获速度提高的水平也受到限制。

2 时频融合优化算法

2.1 时频融合算法

扩展复制重叠捕获算法可以扩大搜索的范围，理论上重叠的段数越多，捕获速度越快，但是由于背景噪声对峰值的影响，段数过多又会影响捕获成功率[8]。而均值捕获方法可以提高相关处理速度，理论上均值的点数越多捕获速度越快，但点数过多同样会使峰值模糊，捕获成功率下降。为此，本文提出一种时频融合捕获法，结合以上两种方法的优势，以达到更优更快的捕获效果。其基本思想是对本地序列进行扩展复制重叠处理，目的是在不影响相关度的基础上扩大搜索范围，然后对处理之后的本地信号以及接收信号进行均值处理，以提高捕获速度，同时在时域上进行载波的多普勒频移的并行搜索。其捕获主要过程如图3所示。

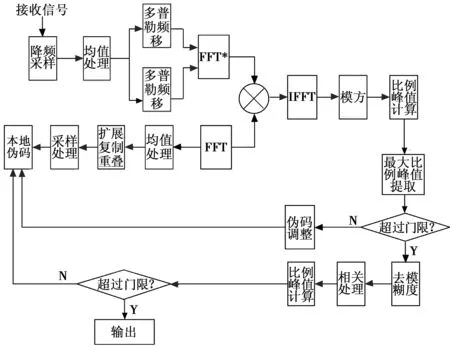
图3 时频融合捕获流程Fig.3 Time-frequency fusion capture process

该算法的原理可行性分析如下。

将一个长为L的接收P码序列表示为A={a1，a2，…，aL}，对该序列补L个零，并且每i个码元取均值，得到序列

(2)

相应地，取长为2L×M的本地伪码样本记为B={b1,b2,…,b2L×M},将其分成M段，每段长为2L,然后将这M段对应位置相加后，每i个码元取均值，可得到序列

(3)

假定伪码的偏移量为0，即假设接收的序列A和序列B在起始位置就达到同步，根据P码良好的自相关特性，只有码元对齐的情况下两个码元{a1b1，a2b2，…，aLbL}的相关值不为0，其余相关值均为无穷小量。那么将序列A′和B′进行相关运算，也只有在偏移量为0的情况下存在{a1b1，a2b2，…，aLbL}项，才存在最大峰值，这和原序列的运算一致，是寻找码片偏移的原理。然后根据展开后每段本地样本和接收信号的相关值，找到具体的码元频偏段数，从而最终确定码片偏移位置。

具体的处理过程如下。

1) 将接收信号中频处理后，以适当的速率、载波频率进行A/D采样和缓存，生成一个长为L的样本G′={g1,g2，…，gL}(L=i×k)。

2) 取L长的接收信号，并对其进行补L个零操作，这样得到一个长为2L的样本，将其记为G″={g1,g2，…，g2L}(gL+1,gL+2，…，g2L=0)，对该样本每i个码元求均值，得到一个新的2K长的样本，记为

G=gq[p]{gq=(g(p-1)i+1+g(p-1)i+2+…+gpi)÷i，p=1，…，2k}2L=i×2k。

(4)

3) 取一定偏移量的长为2L×M的本地扩频伪码样本，将其分成M段，并且将这M段码元对应位置相加，得到一个长为2L的样本。然后再对这个样本进行类似第2)步中的均值运算处理，得到长为2k的样本

(5)

4) 对G进行FFT运算，并取共轭；对F进行FFT运算；将两者处理后的结果相乘，然后进行FFT反变换，对结果取绝对值，即得到相关结果。对相关结果进行采样，并对2k长度内的各峰值进行比较，若超过门限则继续执行，否则，返回重新产生后的本地伪码序列。

5) 去除模糊度，主要包括去除重叠模糊度和均值模糊度。

2.2 时频融合捕获算法的进一步优化

时频融合捕获算法结合了均值法和扩展复制重叠两种方法的优点，进一步提高了捕获速度和捕获精度。但在对多普勒频移的搜索过程中，采用在不同的本地载波偏移下分别进行捕获的验证方法，获得最小相关峰值衰减时的频移，完成多普勒补偿。但是这种方法增加了捕获的搜索量，尤其在高动态的情况下使捕获的速度变得很慢，因此需要做进一步的优化。

为了进一步提高捕获速度，根据时域复指数相乘等于频域偏移的原理，通过移动频域数据序列对多普勒的搜索进行补偿。这种方法不需要在各个本地载波频率偏移下分别进行FFT变换，简化了计算过程，减小了频域变换的计算量，提高了捕获速度，具体的捕获过程如图4所示。

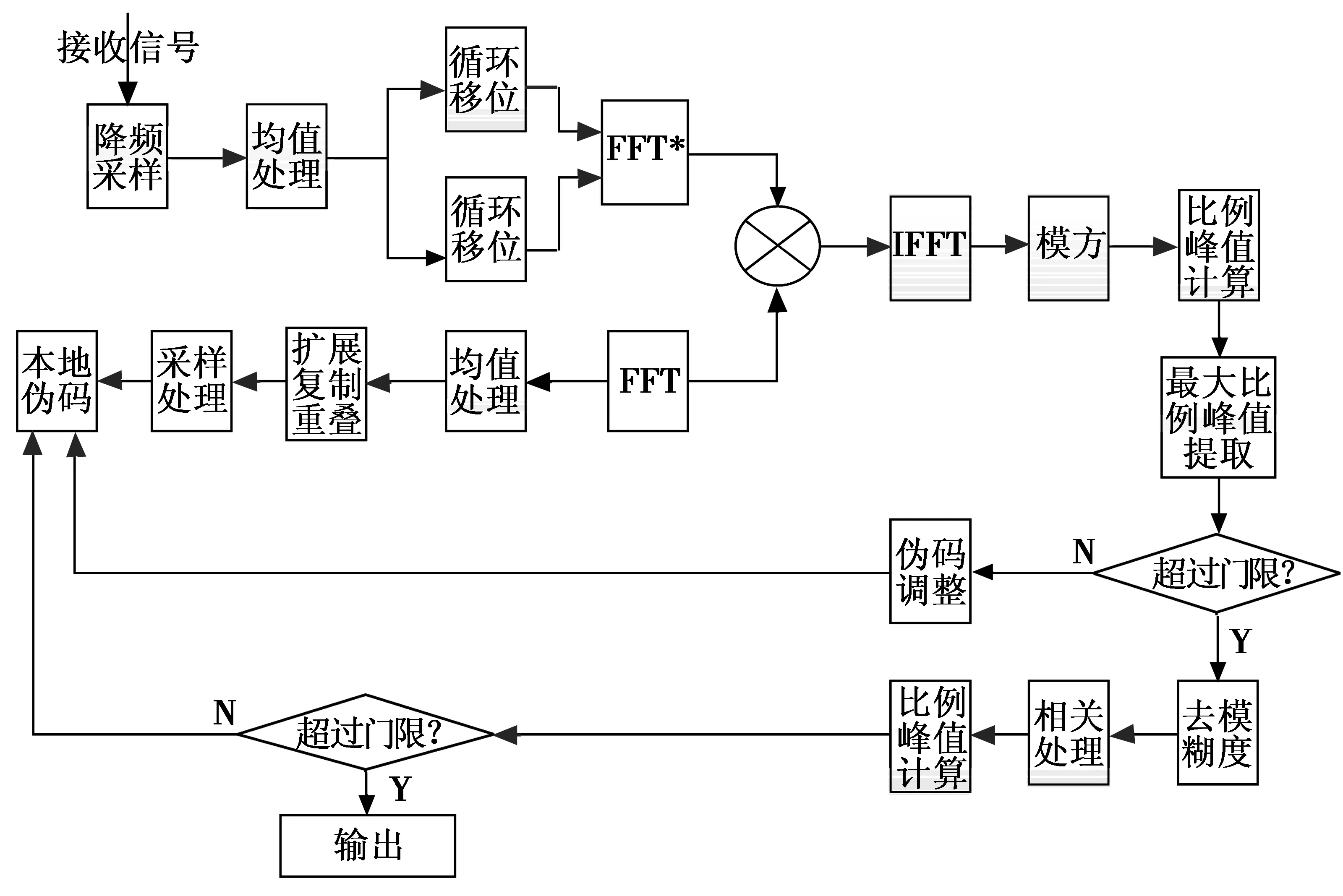
图4 优化算法的捕获过程Fig.4 Capture process of the optimization algorithm

其主要处理方法是将2.1节中的接收序列G进行FFT变换，然后根据多普勒搜索的范围，按照频率搜索精度，将接收信号的FFT变换序列进行N次移位，这样就可以产生N个不同的多普勒补偿后的接收信号的FFT变换序列。之后将补偿后的序列取共轭后同本地处理后的序列相乘，并对其乘积进行IFFT变换，最后进行相关峰值的比较，判定捕获的结果，直到完成捕获。

3 P码直捕算法的仿真分析与比较

对算法的捕获结果以及效能的分析是利用Matlab平台，对优化后P码的直接捕获算法的捕获结果进行仿真，并根据不同捕获方法多次捕获过程的统计分析。仿真参数设定：信噪比为-12 dB，中频频率为20.46 MHz，截短码长为2048。其优化算法的捕获结果如图5所示。

图5 捕获的相关峰值和归一化峰值Fig.5 Captured correlation peaks and normalized peaks

表3、表4分别是时频融合算法及其优化算法捕获结果的统计分析。

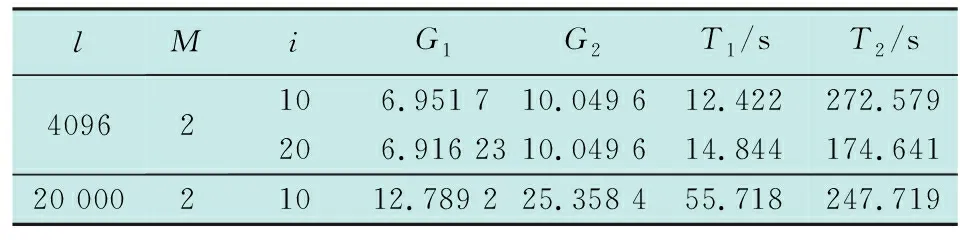
表3 时频融合算法捕获结果

表4 优化算法捕获结果

表5是扩展复制重叠捕获算法、均值捕获算法、时频融合算法以及时频融合优化后的捕获算法在同等参数设置情况下的捕获结果。

表5 不同捕获方法在同等参数下的性能比较

根据捕获性能的统计分析，时频融合算法虽然单次运行时间T1相对扩展复制重叠算法和均值算法较长，但是这种相差很小,只是几秒的差别。然而就总体的捕获时间T2来看，时频融合算法较扩展复制重叠算法捕获时间缩短了一个数量级，较均值算法也缩短了50%左右，捕获速度有了很大的提高。从多普勒误差来看，时频融合算法较扩展复制重叠算法误差要小一个数量级，精度有了很大提高。并且通过对优化算法和时频融合算法的对比可以发现，优化算法的单次运行时间T1和总体捕获时间T2较时频融合算法有一定进步,取得了优化效果，达到快捕的目的。