双排行星齿轮系统的齿轮优化修形∗
2018-10-13张容川周云山胡哓岚程建飞张飞铁
张容川,周云山,胡哓岚,程建飞,傅 兵,张飞铁
(湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082)
前言
不可再生资源的不断消耗和全球温室效应日益突出等环保问题正向我国汽车工业提出了更加严格的要求,而金属带式无级变速器以其经济性、舒适性、操作可靠性和传动平稳性与高效率等优点正逐渐受到整车厂商的青睐。CVT因自身的结构特点和设计要求等,也会存在齿轮机构,特别是本文的研究对象某款金属带式CVT以行星齿轮机构来实现前进挡和倒挡的切换。
由于存在齿侧间隙,行星齿轮系中每一对齿轮副都可能存在3种啮合状态:正常啮合、齿背啮合和空啮合。因此行星齿轮系为一强非线性系统,齿侧间隙会对系统的动态性能产生严重影响,引起齿轮的强烈振动并产生噪声。目前,齿轮的齿廓修形技术能有效改善齿轮的动态性能,削弱齿轮啸叫噪声。国内外学者对于行星齿轮系统的非线性动力学分析和齿轮修形均有不同程度的研究。Kaharaman教授建立了行星齿轮系的纯扭转振动模型[1-2];Velex教授研究了考虑齿形误差和啮合误差的齿轮动态响应[3];孙涛考虑了齿轮啮合间隙和时变啮合刚度建立了2K-H型行星齿轮系统的弯扭耦合非线性动力学模型[10];唐增宝在齿轮动态分析模型的基础上建立了齿轮动态性能的优化数学模型,优化了齿轮的齿廓修形量和修形长度[11];以上研究只是针对行星齿轮系统的运动稳定性或对单对齿轮啮合进行齿轮修形优化。
本文中研究对象为双排行星轮系统,因为只考虑了扭振,所以较单排行星轮系多3个自由度,内部激励更加复杂。本文中主要针对该行星齿轮系进行动态分析,并将其动态性能作为优化指标,确定行星轮的齿廓修形参数,以降低变速器的齿轮啸叫噪声。
1 噪声源的识别
本文中CVT依靠行星齿轮系进行前进挡与倒挡的切换,利用金属带实现动力的传输和速比的变化。动力从输入轴经过行星齿轮系,通过金属带由主动带轮轴传输至被动带轮轴,再经过中间轴传递至差速器输出。其内部结构如图1所示。
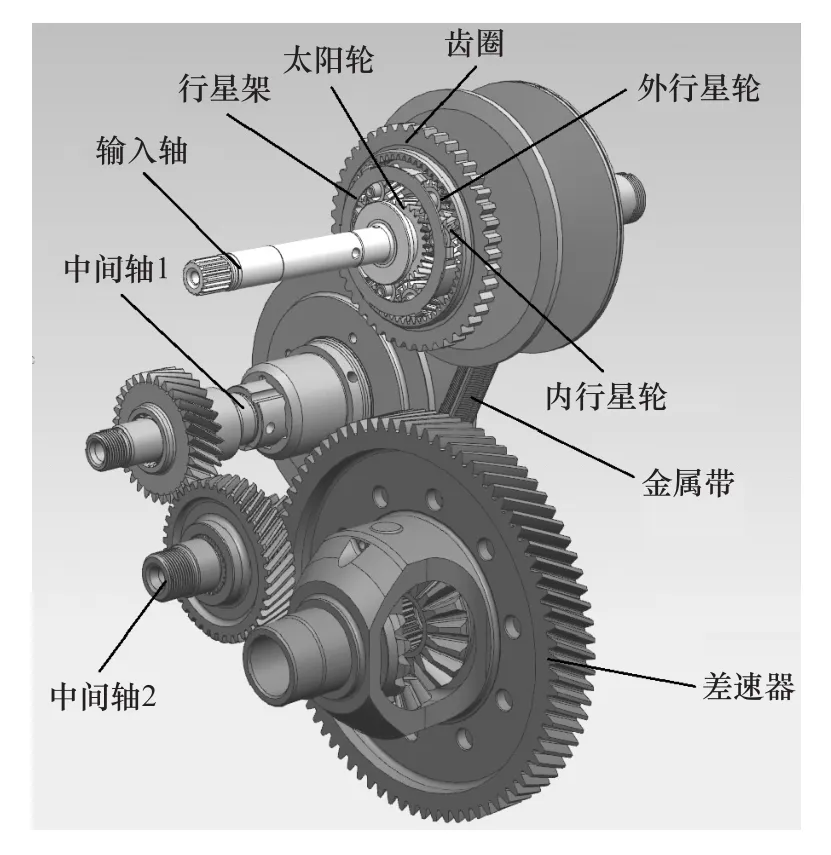
图1 CVT内部结构
倒挡时,行星齿轮系内齿圈固定,动力从输入轴经由太阳轮传递至行星轮,由行星架输出。根据文献[11]关于行星齿轮系的计算可知,行星轮内外啮合频率相等且与输入轴转速关系为

式中:ω为行星轮内外啮合频率;ωs为输入轴转速;zs为太阳轮齿数;zr为齿圈齿数。由式(1)可推算出行星轮阶次为

式中:Op为行星轮阶次;Os为太阳轮阶次;Oshaft为输入轴阶次。
该CVT内各齿轮参数如表1所示。
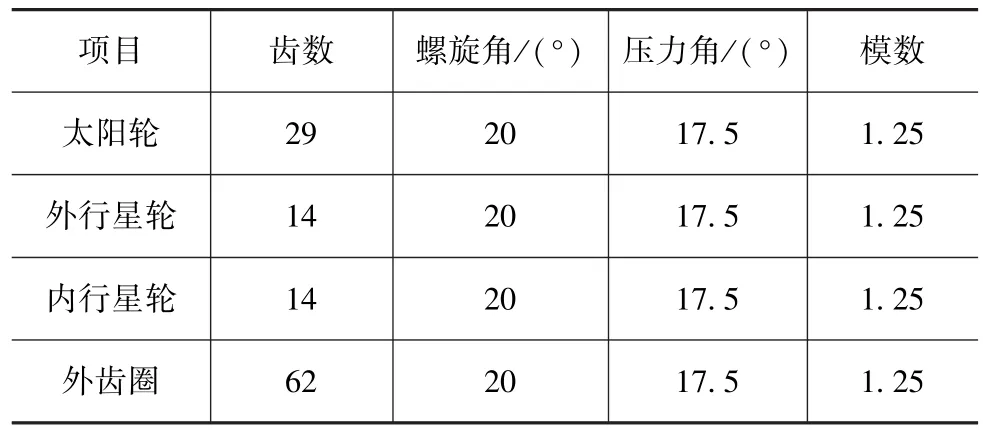
表1 CVT各齿轮参数
将表1中各参数带入公式可计算得出该CVT中各轴及轴上齿轮的阶次,如表2所示。
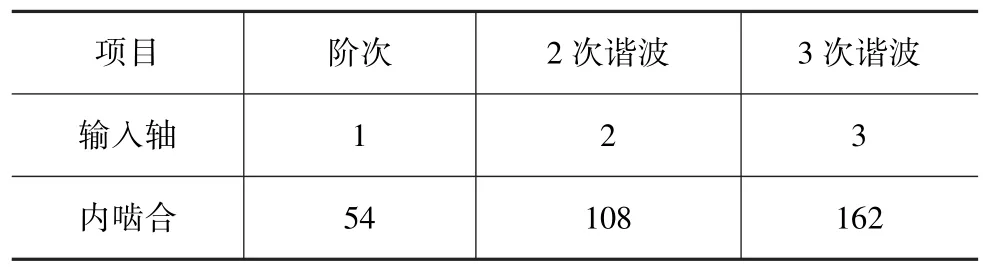
表2 各齿轮及轮轴阶次
对CVT倒挡进行噪声测试实验,在驾驶员右耳处安装声级计,实验结果如图2所示。
由图2可见,在54阶处噪声明显突出,而且在其后还有1条阶次曲线,该阶次为109阶,为54阶次的2倍频。根据上述阶次分析可知,此阶次与该CVT中行星齿轮系统内行星轮的啮合阶次相吻合,因此可判断该CVT倒挡噪声源为其内部的行星齿轮啮合。
2 双排行星轮系统的非线性动力学建模
2.1 行星轮的纯扭转模型
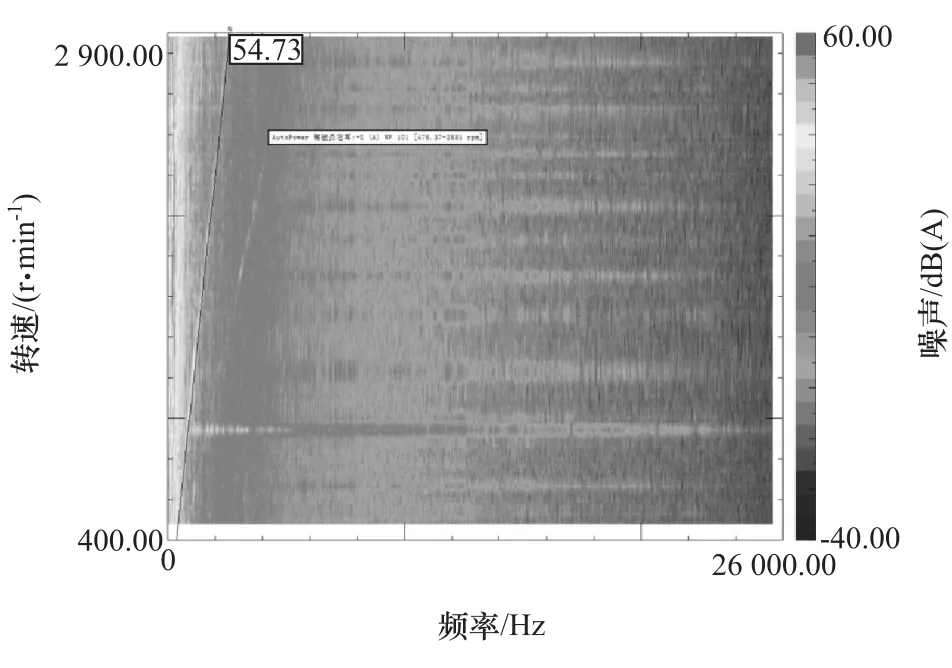
图2 驾驶员右耳处噪声
Kahraman研究发现,在构建的支撑刚度与啮合刚度之比大于10时,纯扭转模型与弯扭耦合振动模型在动力学响应上可以等价[2],因此可以不考虑各部件的轴向振动。另外,由阶次分析可知,该CVT倒挡时主要噪声源来自行星轮的啮合,所以本文中研究的重点在于行星轮的扭振运动,在本小节将只对该行星轮系建立纯扭转振动模型。
行星轮系的扭振模型如图3所示。图中,S为太阳轮,PIi为内排第i个行星轮,Poi为第i个外排行星轮,R为齿圈,C为行星轮架。各齿轮均为圆柱斜齿轮。
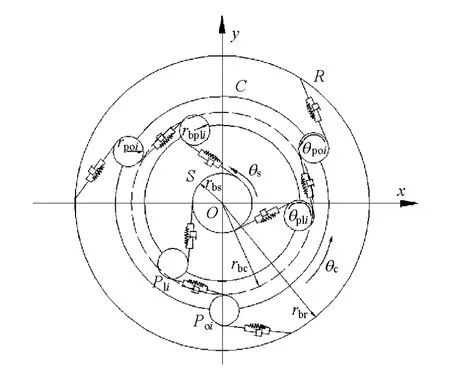
图3 双排行星轮系统纯扭转振动模型
2.2 时变啮合刚度
由文献[12]可知,尽管斜齿轮啮合刚度随时间的变化比直齿轮更加平稳,但仍然具有周期性,在某均值附近做微小波动。同时由文献[16]可知,将此波动近似为矩形波动,则该行星轮系内、外行星轮分别与太阳轮和齿圈啮合的内、外啮合刚度及其之间相互啮合的啮合刚度变化规律均可表示为矩形波,如图4所示。
将其分别展开为以啮合频率ω为基频的傅里叶级数,取1次谐波:
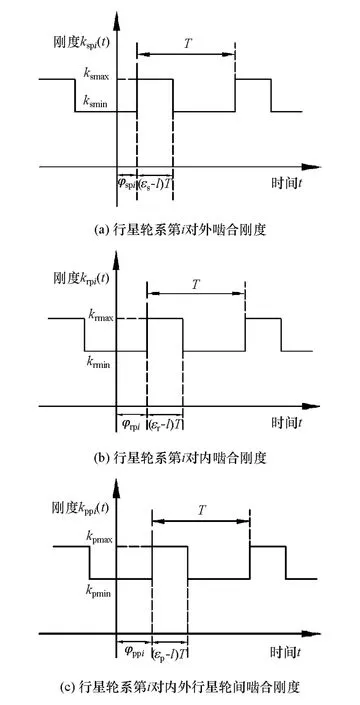
图4 双排行星轮系啮合刚度变化规律
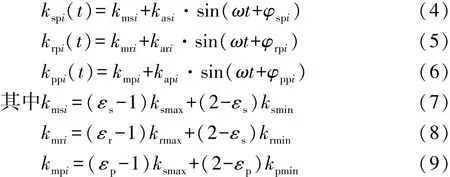
式中:kmsi为第i路外啮合刚度;kmri为第 i路内啮合刚度;kmpi为第i路行星轮间啮合刚度。
2.3 综合啮合误差
行星齿轮系内齿轮副的综合误差来源有齿轮副的齿形误差、齿轮副的基节误差和齿廓的修形量。齿形误差为

式中:A为齿形误差幅值;ω为啮合频率;β为齿轮误差相位角。
本文中采用齿廓修形,对太阳轮进行齿顶修缘,如图5所示。
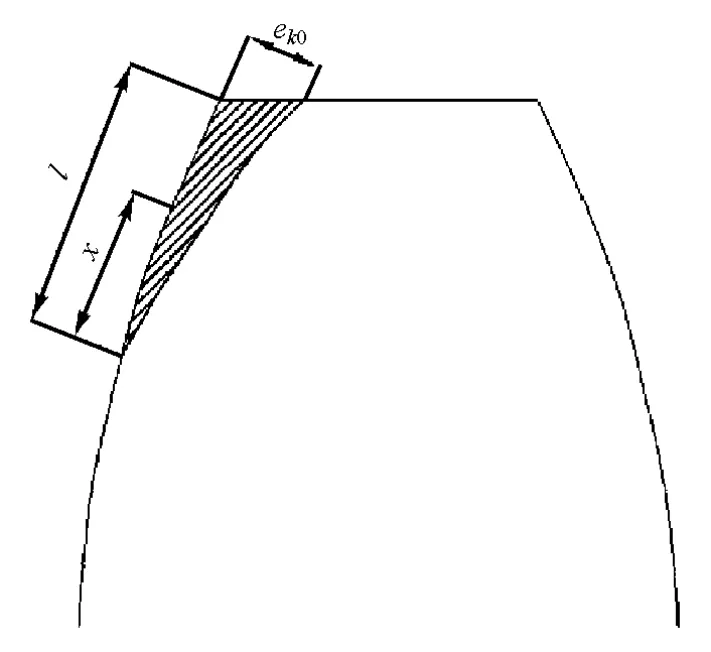
图5 齿顶修形示意图
以啮合线上修形起始点为原点,则对于啮合线上任意点xk,对应在齿廓方向上为距离x,则对应的修形量为

式中:ek0为齿顶最大修形量;l为齿廓方向的修形长度,其对应在啮合线方向的度量为lk;n为修形曲线的指数。结合式(10)和式(11)可列出该行星轮系各对齿轮副的综合啮合误差:
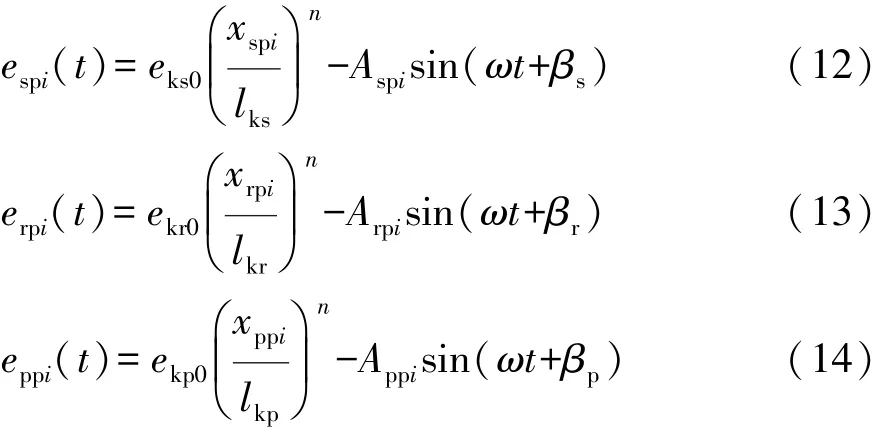
2.4 动态啮合力
在行星齿轮系传动过程中,各对齿轮副存在3种啮合状态:正常啮合、空啮合和齿背啮合[13],因此,引入具有齿侧间隙时齿轮副啮合力对应的非线性函数,如图6所示,其表达式为
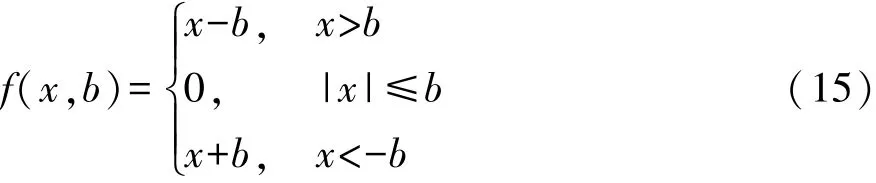
式中:x为啮合点相对位移;b为齿侧间隙。
对于行星轮系内各对齿轮副,其啮合点相对位移分别为 xrpi,xspi和 xppi:

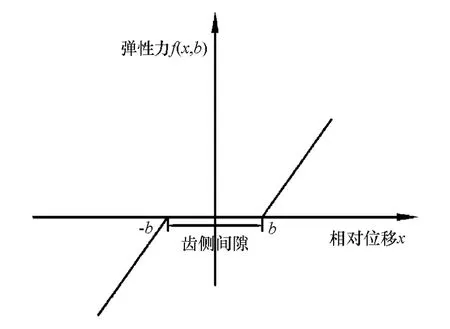
图6 齿侧间隙非线性函数
式中:xc为行星架 rcθc在啮合线上的投影,即 xc=rcθccosα;xs,xpo和 xpi分别为太阳轮、外行星轮和内行星轮在啮合线上的线位移。由此,可得到该行星轮系第i路各齿轮副上的动态啮合力为
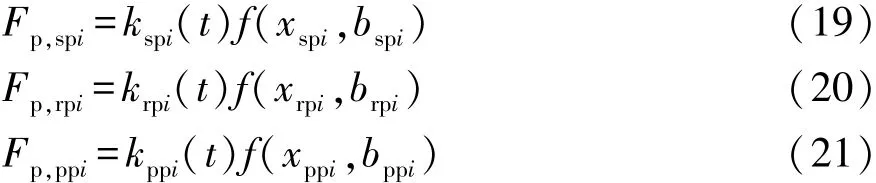
各齿轮副第i路啮合阻尼力为

式中:cspi,crpi和 cppi分别为外啮合、内啮合和双排行星轮间啮合阻尼系数;ζs,ζr和 ζp分别为外内啮合以及行星轮之间相互啮合的相对阻尼比;ms为太阳轮质量;mpIi为内排行星轮质量;mpoi为外排行星轮质量;mr为齿圈质量。
2.5 振动微分方程
将输入转矩作用下各个齿轮的转动方向规定为正方向,得到该行星轮系的非线性动力学方程如下:
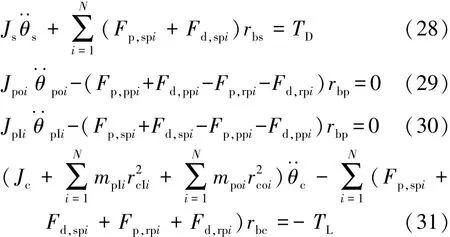
式中:i=1.2,…,N;Js为太阳轮转动惯量;JpIi为内排行星轮转动惯量;Jpoi为外排行星轮转动惯量;Jc为行星架转动惯量;rcIi为内排行星轮中心到太阳轮中心距离;rcoi为外排行星轮中心到太阳轮中心距离;rbp为行星轮基圆半径;rs为太阳轮基圆半径。
由于考虑了齿侧间隙,式(28)~式(31)所列方程为强非线性方程,无法利用叠加原理进行求解。对于齿轮间隙的非线性方程,由文献[13]可知,数值解法是可行的方法。将行星轮系内各齿轮参数带入方程,运用4阶龙格库塔法对方程进行求解,得到太阳轮啮合线上位移响应,如图7所示。
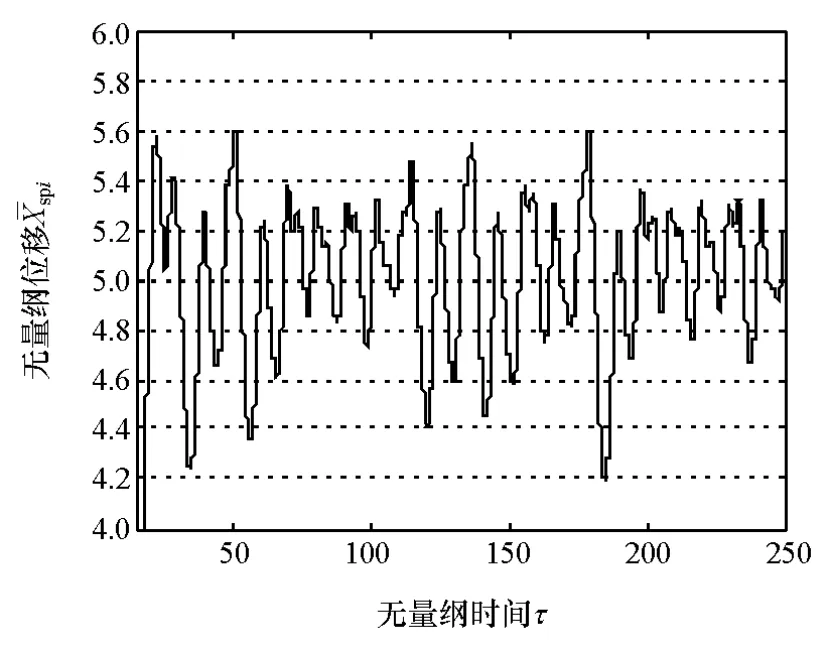
图7 太阳轮在啮合线上位移响应
需要注意的是,图中横纵坐标均为无量纲化后的时间轴和位移轴,其值并不是实际的时间和位移量,但可以反映该行星轮系的扭振规律。
3 基于遗传算法的齿轮修形量优化
3.1 优化目标和设计变量
本文中研究目的在于降低行星齿轮系的齿轮振动和噪声,根据文献[14]可知,齿轮扭转振动的加速度均方根值与齿轮噪声成线性关系,再联系2.5节所述,将其作为优化目标。
本文中主要采取齿廓修形来进行降噪,因此将齿顶修形量ek和修形长度l作为设计变量。
3.2 遗传算法与问题分析
遗传算法是一种人工智能算法,它是在计算机上模拟生物进化过程的一种搜索寻优算法。其基本思路是:将函数的搜索空间作为一个映射的遗传空间,将此空间内的可行解看作由向量染色体组成的集合,对集合内每个个体通过构造适应度函数进行筛选,再通过交叉、变异等操作生成新的个体,再继续通过适应度函数优胜劣汰,如此不断循环直到满足终止条件。
与传统优化算法相比,遗传算法具有以下优点:对目标函数仅要求有定义,而不需要导数等信息;遗传算法为全局搜索,降低了收敛于局部最优解的可能性;具有隐含并行处理性等。
由3.1节所述和2.5节中振动微分方程可知,目标函数与设计变量间为隐式关系,且2.5节中扭振方程因考虑了齿侧间隙,为强非线性方程,几乎不可能得到精确的解析解,大多数研究者都采用数值法进行求解。传统的优化算法需要精确的目标函数,因此不适合本文中所研究的问题,而遗传算法对目标函数的要求不高,只须构造相应的适应度函数,计算每个个体的适应度即可,因此本文中将采用遗传算法对齿轮的修形量进行优化。
3.3 构造适应度函数
齿轮扭振加速度的均方根值与齿轮噪声成线性关系,且大于零,符合同时适应度函数必须大于零的要求,因此直接将太阳轮与内行星轮啮合线上相对位移作为适应度函数:
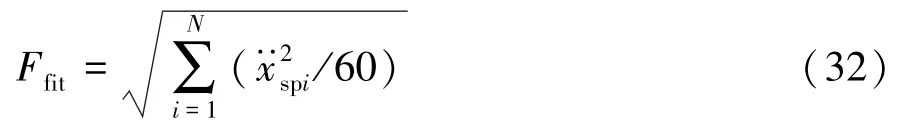
3.4 约束条件
约束条件为

式中:Emin和Emax分别为齿顶最小、最大修形量;Lmin和Lmax分别为最小、最大修形长度。
3.5 优化结果
利用MATLAB里的遗传算法工具箱对齿轮修形参数进行优化,其参数设置如图8所示。
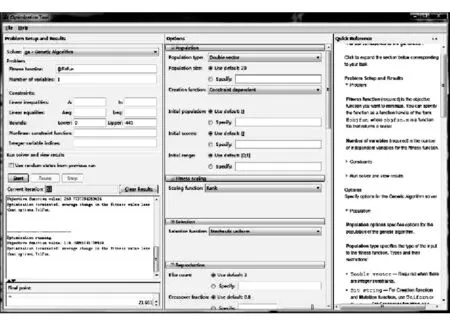
图8 MATLAB遗传工具箱设置
经过63次迭代后,得到最佳的齿廓修形参数齿顶最大修形量ek0=0.007mm,齿廓方向的修形长度l=0.3794mm。将优化后的修形参数代入式(28)~式(31),同样地,仍然利用4阶龙格库塔法进行数值求解,可得太阳轮与内行星轮啮合线上振动加速度随时间的变化曲线,如图9所示,可看出修形后其扭振强度削弱了。
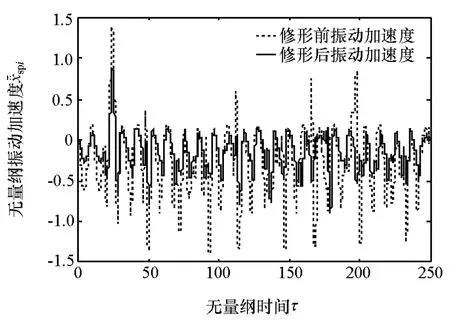
图9 修形前后太阳轮振动加速度
4 实验验证
为验证齿廓修形的正确性,按照3.5节优化结果的修形参数对齿轮进行修形,并安装在CVT中,对该CVT进行实车实验,测量搭载该CVT后驾驶室内的噪声值,如图10所示。

图10 测试实验
在该CVT的悬置安装位置上的被动点和主动点分别装一个加速度传感器测量其振动,如图11所示。
将实验所得的原始时间信号在Test.Lab里进行FFT变换,并追踪输入轴转速得到噪声值的瀑布图,如图12所示。
由图可见,54阶阶次噪声幅值降低。为对比修形前后效果,取54阶的切片图得到该阶次曲线,与修形前该阶次进行对比,如图13所示。

图11 加速度传感器安装位置
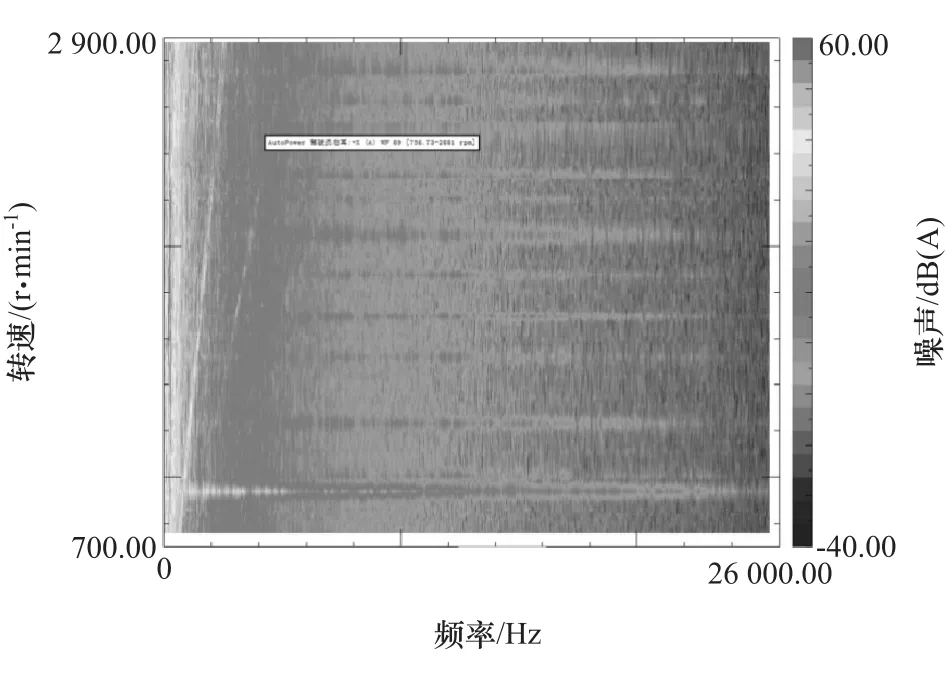
图12 修形后噪声瀑布图
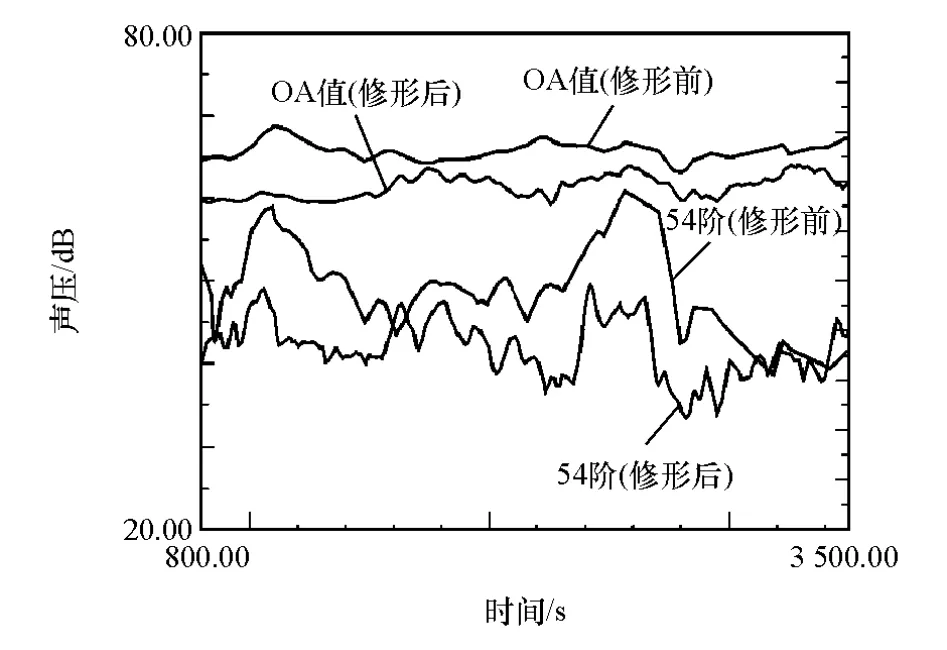
图13 修形前后噪声OA值和54阶次切片
从图13中可以看出,在54阶次的阶次噪声比修形前有一定的削弱,且总声压级也减小了1dB左右,说明对齿轮修形量的优化起了作用。
5 结论
(1)通过实验与阶次计算推断出该CVT倒挡的啸叫噪声来自其内部双排行星轮机构内齿轮啮合。
(2)考虑齿侧间隙,对该双排行星轮系建立了纯扭转振动的非线性数学模型,并运用龙格库塔法进行数值求解。
(3)运用遗传算法对齿轮的齿廓修形参数进行优化,并将按该参数进行齿轮修形的CVT进行实车测试,发现该CVT的倒挡阶次噪声降低了约3~4dB(A)。
本文中所建立的模型为纯扭转模型,忽略了该行星轮系的横向振动,同时,本文中假设时变啮合刚度为周期矩形波,在实际情况中斜齿轮啮合的时变啮合刚度会更加复杂,对斜齿轮的时变啮合刚度进行更加精细的建模和实验验证将是今后的研究方向。
