自动驾驶汽车横向可拓预瞄切换控制系统研究∗
2018-10-13蔡英凤孙晓强江浩斌何友国
蔡英凤,臧 勇,孙晓强,陈 龙,王 海,江浩斌,何友国
(1.江苏大学汽车工程研究院,镇江 212013; 2.江苏大学汽车与交通工程学院,镇江 212013)
前言
汽车智能化技术作为解决交通安全、交通拥挤和环境污染问题的重要手段,正引发世界各国的新一轮角逐,受到各国学者的广泛关注。自动驾驶作为智能汽车发展的高级阶段,其核心之一是横向控制系统。车辆横向控制是指车辆在沿着期望路径行驶过程中,通过算法决策和底层执行装置的作用[1],使横向位置偏差和航向偏差尽可能小,同时车辆应具有一定的稳定性和行驶安全性[2]。目前使用的横向控制算法有经典控制[3-4]、最优控制[5]、自适应控制[6]、滑模控制[7]、模型预测控制[8-9]和模糊控制[10]等方法。
自动驾驶车辆横向控制要求车辆自主转向过程中满足两个要求:横向位置偏差为零和航向偏差为零[11]。以当前车辆的运动状态为基础,通过预瞄车辆即将行驶到的前方某个位置,得到车辆与期望路径之间的横向预瞄偏差,再调节车辆前轮转角,使车辆跟踪期望路径,实现自动驾驶车辆的横向控制[12-13]。然而上述控制方法控制器的约束条件较多,有效控制区域小,在某些工况下控制效果不佳,尤其对于道路曲率变化范围大的混合工况,会出现求解失败和控制误差大的问题。除经典控制方法外,大多数控制器计算量大、迭代速度慢,对于硬件要求高,实车移植性差。
基于蔡文提出的可拓理论[14],产生的可拓控制能够描述事物“是”与“非”的相互转化和量变与质变过程,可用于描述系统失稳与稳定之间的关系,并据此建立针对不同系统状态区域,实现多种控制器切换控制,可以拓展高精度控制区域,在较大范围内满足控制精度要求。基于此,本文中针对单一控制策略控制区域有限的问题,设计了一种自动驾驶汽车横向可拓预瞄切换控制系统。根据车辆在道路中所处的状态,将车辆 道路系统状态划分为3个区域:经典域、可拓域和非域。经典域中车辆所在道路曲率小,且车辆与目标轨迹之间横向位置偏差小,此时整个车辆 道路系统稳定,采用简单的PD反馈控制即可;可拓域中道路曲率和车辆与道路中心线之间的横向位置偏差都变大,整个车辆 道路系统濒临失稳状态,须加快前轮转角的响应速度,可采用PD前馈 反馈控制策略,利用前馈控制校正PD反馈控制的时滞性,加快响应速度[15]。
1 车辆动力学和路径跟踪误差模型
1.1 2自由度车辆动力学模型
本文中采用2自由度车辆动力学模型,该模型只考虑沿车辆y轴的侧向运动和绕z轴的横摆运动,沿车辆x轴方向的速度为定值,车辆2自由度动力学模型如图1所示。根据牛顿第二定律定理,可得到车辆2自由度动力学方程[16],即沿y轴的力平衡方程和绕z轴的力矩平衡方程:

式中:m为车辆质量,kg;vx和vy分别为车辆纵向速度和侧向速度,m·s-1;φ 为车辆航向角,rad;φ·为车辆绕z轴横摆角速度,rad·s-1;δf为车辆前轮转角,rad;Iz为车辆绕 z轴的转动惯量,kg·m2。
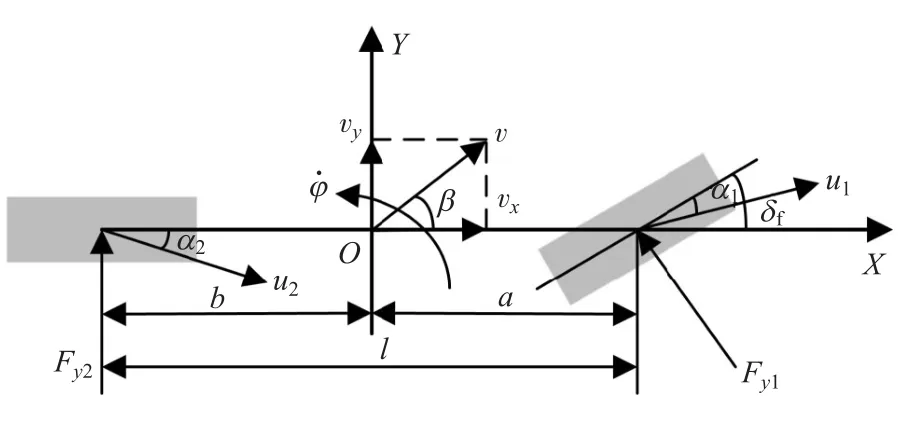
图1 2自由度车辆动力学模型
1.2 路径跟踪预瞄误差模型
横向预瞄误差模型如图2所示,图中:C点为车辆质心;D点为预瞄点;a和b分别为车辆前轴距离和后轴距离,m;L为预瞄距离,m;ep为预瞄点的横向偏差,m;φr为车辆与道路中心线的航向偏差,rad。

图2 横向预瞄误差模型
根据几何关系[17]可得

航向偏差模型如图3所示,图中φd为道路中心线切线与大地横坐标的夹角,rad。
根据图3所示几何关系[17]可得

图3 航向偏差模型

因此,可得到车辆状态量侧向速度vy、侧向加速度v·
y、车辆横摆角速度、车辆横摆角加速度与预瞄偏差模型中的参数关系[18]:

将车辆2自由度动力学模型与路径跟踪偏差模型相结合,建立车辆-道路模型,选取e,,φ 和pr为状态空间方程的状态量,得到车辆-道路模型具有=Ax+Bu形式的状态空间方程:

2 可拓预瞄切换控制系统设计
2.1 控制器系统设计
横向可拓预瞄切换控制系统包括上、下层控制器,系统结构如图4所示。图中ρ为道路中心线曲率。
上层控制器为可拓控制器,主要目的是根据参数ep与ρ,将车辆横向控制所处的状态划分为经典域、可拓域和非域3个区域[14]。对于不同的车辆-道路系统的状态,分别采用不同的控制策略,实现在经典域和可拓域控制方法的切换。
在下层控制器中,当车辆-道路系统状态处于经典域时,ep和ρ都较小,车辆-道路系统状态稳定,采用简单PD反馈控制器即可。当车辆-道路系统状态处于可拓域时,ep和ρ较大,为加快前轮转角响应速度,解决PD反馈控制滞后问题,须在原有PD反馈控制方法的基础上,增加基于道路曲率的前馈校正,构成PD前馈-反馈控制。
2.2 上层可拓控制器设计
上层可拓控制器包括特征量提取、可拓集合划分、关联函数计算和测度模式划分4个部分。
(1)特征量提取

图4 可拓横向预瞄控制系统
可拓控制区域划分与车辆-道路系统状态相关,评价自动驾驶车辆横向控制的基本指标为ep和ρ,同时控制系统策略的设计与道路情况密切相关,反映道路基本状况的指标为ρ,因此,选ep和ρ作为可拓控制器特征量,并组成特征状态S(ep,ρ)。
(2)可拓集合划分
ep由摄像头等传感器采集获得,可拓集合可拓区域应在摄像头可靠工作的范围内,同时结合实际车辆行驶状况,通过多次试验确定可拓域ep的最大容许范围为(-2,2)m;ρ最大容许范围为(-0.12,0.12)m-1。针对经典域,采用控制策略为简单PD反馈控制,控制范围有限,通过多次实验发现在ρ达到0.01而ep达到0.1时,PD反馈控制开始出现较大的跟踪偏差。因此,经典域的ep最大容许范围确定为(-0.1,0.1)m,ρ最大容许范围为(-0.01,0.01)m-1,建立如图5所示的二维可拓集合[19]。
(3)关联函数计算
传统可拓控制器选取的特征量为偏差和偏差微分,本文中选取ep和ρ为特征量,须按照蔡文提出的可拓学理论计算可拓距,以确定关联函数值。
在二维可拓集合中,原点(0,0)为特征状态的最优点,如图5所示。假设可拓域中存在一点P3,连接原点与P3点,获得P3趋近最优点(0,0)的最短距离|OP3|。该线段所在直线交经典域边界于P1和P4点,交可拓域边界于P2和P5点。在保证P3趋近于原点距离最短的前提条件下,根据这些交点即可确定P3与可拓域和经典域的最短距离[20]。

图5 二维可拓集合
根据蔡文的可拓理论,在一维可拓集合中,可拓距实质为点到区间边界的最小距离,根据这一原理可将二维可拓集合中的可拓距转化为一维可拓距,如图6所示。

图6 一维可拓集合
P3点到经典域和可拓域的可拓距分别为ρ(P3,〈P4,P1〉)和 ρ(P3,〈P5,P2〉)。 以 ρ(P3,〈P4,P1〉)为例,求解如下:

同理求解 ρ(P3,〈P5,P2〉),然后可确定关联函数:
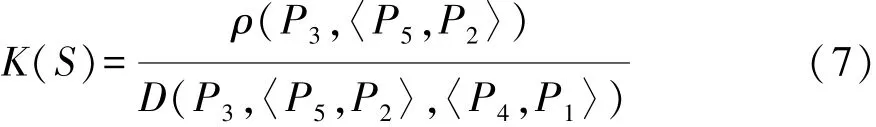
其中:
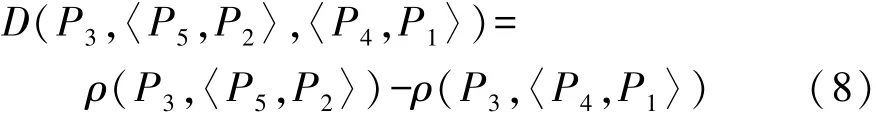
(4)测度模式划分确定控制策略
根据上述关联函数的求解结果K(S),选择对应的控制策略[21]:
当K(S)≥1时,特征状态S(ep,ρ)处于经典域中,采用PD反馈控制策略;
当 0≤K(S)<1 时,特征状态 S(ep,ρ)处于可拓域中,采用基于曲率的PD前馈-反馈控制策略;
当 K(S)<0时,特征状态 S(ep,ρ)处于非域中,自动驾驶车辆处于完全不可控状态,采取紧急制动。
2.3 下层控制器设计
经典域中采用如图7所示的基于预瞄偏差的PD控制,预瞄偏差包含横向位置偏差和车辆航向与道路期望航向之间的航向偏差,同时调节这两个偏差以获得合适的前轮转角输入[22],满足车辆横向控制偏差尽可能小的要求。设计时通过加权的方式来实现两者偏差调节量的叠加[23-24]。

图7 基于预瞄偏差的PD反馈控制器控制流程图
可拓域中为提高响应速度,减少迟滞反应,采用如图8所示的基于道路曲率的PD前馈-反馈控制器控制,基于前方道路曲率的PD前馈-反馈控制加快大转角情况下车辆前轮转角响应,提高控制系统对于小曲率路径的响应速度,可有效减小车辆转向控制的滞后性和波动性[25]。
3 Simulink仿真分析
本文中所采用的汽车整车参数如表1所示。通过Simulink搭建的仿真模型如图9所示。

表1 整车参数

图9 Simulink仿真模型
为验证所提出的可拓预瞄切换控制方法对时变曲率非常态道路的适应性,此处道路工况曲率设置为三角函数,曲率随时间的变化如图10所示,系统响应结果如图11~图16所示。

图10 道路中心线曲率曲线

图13 横向位置偏差
由图11可见:关联函数K(S)在(0,+∞)范围内变化,在0~5s范围内道路为直线道路,此时车辆-道路系统为稳定状态,关联函数值稳定于1.08左右,处于经典域中;随着道路曲率的增加,K(S)值逐渐减小进入到小于1的范围内,系统从经典域进入可拓域中,实现两种区域内的切换控制,此处,关联函数值的变化实时体现了车辆-道路系统的稳定状态,对整个控制系统有较好的监控作用。

图14 航向偏差

图15 侧向加速度

图16 横摆角速度
由图13和图14可见,车辆在经过最大曲率处时,横向偏差在0.15m左右,航向偏差峰值在0.1rad左右,保持了较高的跟踪精度。由图15和图16可见,除在切换点处存在一定的抖动峰值外,侧向加速度在±3m/s2范围内,横摆角速度在±0.6rad/s范围内,因此车辆在轨迹跟踪过程中,侧向稳定性满足基本要求。
仿真结果表明,本文中提出的可拓预瞄切换控制系统在时变大曲率变化道路工况下有较好的适应性和可靠性。
4 试验研究
试验系统为自主研发的智能驾驶平台,如图17(a)所示,系统包括5个部分:车道线采集系统、车身状态信息采集系统、上位机控制系统、下位机控制系统和PC机监视界面。试验工况为S弯道,模拟场景如图17(b)所示,初始速度为0,稳定车速为2m/s,初始的位置横向偏差和航向偏差皆为零,试验结果如图18~图20所示。

图17 自动驾驶试验平台和试验模拟场景
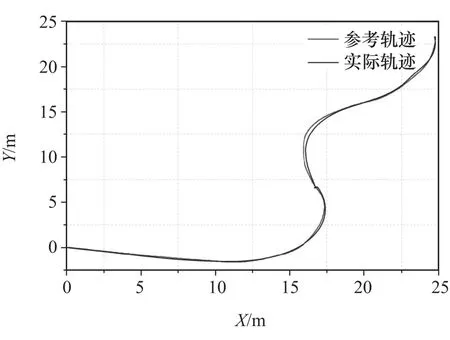
图18 弯道轨迹跟踪效果
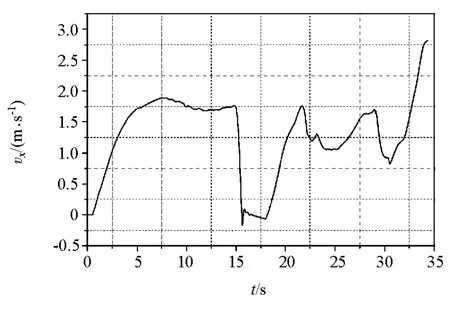
图19 车辆纵向速度

图20 车辆侧向加速度

图21 车辆横摆角速度
由图18可见,在车辆进入弯道最小转弯半径处,产生的偏差略大,且在弯道换向处汽车产生运动轨迹的扭曲,此处由于汽车进行了大转角的换向动作,导致车辆出现急停现象,随着车辆动作调整,继续完成轨迹跟踪运动。由图19可见,汽车速度整体稳定在2m/s左右,但在汽车经过S弯换向处出现一次急停情况,这是由于此时汽车弯道换向时需要大转角响应,汽车响应速度稍慢,导致汽车触发急停。由图20可见,汽车在经过S弯时侧向加速度变化范围为-1~1m/s2。由图21可见,除在汽车经过S弯换向处大转角产生的横摆角速度峰值为7°/s外,其余点变化范围为-2.5~2.5°/s,无人驾驶汽车在经过S弯时,除最大转角处出现轻微抖动外,整体运动较为平稳,满足控制稳定的基本要求。
5 结论
本文中根据车辆与道路中心线的横向位置偏差和前方道路曲率两个状态量,基于可拓控制理论将车辆-道路系统状态分为经典域、可拓域和非域3个状态,在对应的域中分别采用PD反馈控制、PD前馈-反馈控制和紧急制动控制,仿真结果表明,所采用的方法实现了横向控制系统在经典域和可拓域中两种控制策略的切换控制,一方面保证了车辆在通过大曲率道路工况的跟踪精度,另一方面也改善了在小曲率道路工况下跟踪性能,从而拓展了高精度控制区域,并通过关联函数值直观体现了系统的稳定性。最后,通过自动驾驶汽车试验,初步验证了本文中提出的控制系统的有效性。因此,本文中提出的自动驾驶汽车横向可拓预瞄切换控制系统对于时变大范围曲率道路有较好的适应性和可行性,具有一定的发展前景。
