自动变速器表面涂层齿轮温度场特性的仿真与试验研究∗
2018-10-13臧立彬周慧东罗大国
臧立彬,陈 勇,陈 华,刘 海,周慧东,李 凯,罗大国
(1.河北工业大学机械工程学院,天津 300130; 2.吉利汽车动力总成研究院,宁波 315000)
前言
随着汽车技术的发展和节能环保的要求,小型化、轻量化、多挡位、宽速比和高效率成为汽车自动变速器的发展趋势。齿轮是汽车传动系统的重要部件,要求进一步提高其齿面强度和耐热胶合性能,改善动力传动性能和实现小型化目标,以适应自动变速器技术的发展[1],这对变速器齿轮表面强度提出了更为苛刻的要求,除化学热处理外,表面涂层技术在变速器齿轮表面的应用越来越受到产业界的重视,同时也成为学术界的研究热点[2-3]。在齿轮啮合过程中,轮齿啮合面因摩擦而产生热流量,同时还受润滑油的强制对流传热等因素的影响,齿轮的热平衡状态与温度和齿面瞬时温度的变化极为复杂。对于齿轮温度场仿真计算,国内外学者做了大量的研究工作,主要集中在数值计算[4-5]和有限元仿真[6-7];TABURDAGITAN M等研究了摩擦热对齿面啮合温度的影响[8];石万凯等对重载齿轮涂层的承载能力进行了仿真分析[9]。近年来,有限元法在齿轮温度场计算中得到广泛应用,但大多集中于直齿轮,且未考虑齿轮表面涂层的影响。综合考虑涂层特性、摩擦热流密度和对流传热系数加载方式的变速器齿轮温度场数值仿真还不多见。因此,在变速器齿轮系统的设计初期,综合考虑齿轮表面涂层对齿轮传动性能的影响,对变速器齿轮的抗疲劳、抗胶合的设计至关重要。
为揭示表面涂层对变速器齿轮抗疲劳失效的影响机理,本文中通过电化学沉积的方法在齿轮表面制备不同厚度的磷酸锰转化涂层(Mn-P),通过摩擦磨损试验获得涂层与非涂层试件的滑动摩擦因数;选取某7速双离合自动变速器1挡齿轮为研究对象,通过考虑热量分配和载荷分配,准确计算出斜齿轮副在不同啮合位置的摩擦热流密度;基于有限元方法对不同厚度涂层的齿轮进行温度场的数值模拟,获得涂层处理前后齿轮的稳态温度场分布规律,并通过红外热成像仪进行齿面温度测量,验证了齿轮传动温度场仿真结果的准确性。研究结果对自动变速器齿轮的抗疲劳强度设计与齿轮表面完整性学术研究具有重要意义。
1 涂层齿轮齿面发热量计算
1.1 接触面摩擦热流密度
齿轮表面的摩擦热流密度由齿面接触压力、相对滑动速度和齿面摩擦因数共同决定。齿轮在啮合过程中的摩擦主要有:滑动摩擦、滚动摩擦和金属弹塑性变形引起的内摩擦。由于相对于滑动摩擦,滚动摩擦和金属弹塑性变形引起的内摩擦产生的热量很少[7],所以在本文的计算中忽略不计。齿面的摩擦热流密度为

式中:qc为摩擦热流密度;ξ为热能转换系数,一般取值为0.90~0.95;f为摩擦因数;p为啮合点的接触压力;Vsc为啮合点的相对滑动速度。
在任意啮合位置,主、从动齿轮的摩擦热流密度为
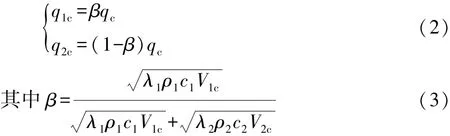
式中:β为主、从动齿轮摩擦热的分配系数;λ1,λ2为主、从动齿轮材料的导热系数;ρ1,ρ2为主、从动齿轮材料的密度;c1,c2为主、从动齿轮材料的比热容;V1c,V2c分别为主、从动轮的切向速度。
1.2 摩擦热流密度的参数计算
1.2.1 齿轮接触压力
根据赫兹接触理论,不考虑端面效应,两圆柱体表面线接触平均接触应力pn为

式中:F为接触面上的总压力;L为两圆柱接触线长度;R1,R2分别为两圆柱半径;E1,E2分别为两圆柱材料的弹性模量;ν1,ν2分别为两圆柱材料的泊松比。
斜齿轮的接触状态不像直齿轮一样直接等效为赫兹接触。为此本文中将斜齿轮沿螺旋线分成无数齿轮薄片,斜齿轮接触可视为无数直齿轮薄片的接触。将齿面接触线平均线载荷计算公式和齿轮的综合曲率半径公式导入赫兹接触公式中,可得斜齿轮齿面任意接触点i的平均接触压力为

式中:WK为沿齿面接触线上单位长度的法向载荷,WK=Fnc/L,Fnc为接触齿面的法向载荷,L为齿轮接触线长度,为端面重合度,b为齿宽,βb为基圆螺旋角;E为齿轮等效弹性模量;Re为齿轮综合曲率半径;ν为泊松比。
斜齿轮的啮合过程中法向啮合力Fnc随着啮合齿对数和啮合点的变化而变化,为便于计算,取啮合点在节圆位置时的法向啮合力作为轮齿齿面的平均法向啮合力Fnc:

式中:T为输入转矩;r1为主动轮节圆直径;Z1,Z2分别为主、从动轮的齿数;αn为法向压力角;β为节圆螺旋角。
1.2.2 平均摩擦热流量
主动轮啮合面上的啮合点i在稳态情况下温度和载荷皆呈现周期性的变化,接触面的相互摩擦使接触点的温度迅速升高,随着润滑油的对流换热和齿轮的热传导作用,在不考虑外界条件影响的情况下,每个啮合周期里的温度变化趋势也相同,最高温度为齿面的瞬时接触温度tc,最低温度为齿轮传动系统的本体温度tm,最大温升即为闪点温度tf:

主动轮和从动轮任意啮合点在每个周期内的平均摩擦热流量Qk1和Qk2为

式中:T1和T2分别为主动轮和从动轮啮合周期;τ1和τ2分别为啮合位置处主动轮和从动轮从开始接触到接触宽度为2a所需时间,a为齿轮的接触半宽。
1.2.3 轮齿间相对滑动速度
主、从动轮啮合点的切向速度分别为

式中:n1,n2分别为主、从动齿轮的转速;R1i,R2i分别为主、从动齿轮的节圆半径。
则齿轮啮合点的相对滑动速度为

图1为计算得到的啮合点处主、从动齿轮的切向速度和相对滑动速度。
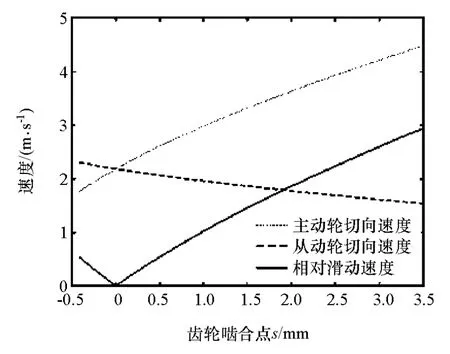
图1 齿轮啮合点的相对滑动速度
1.3 涂层摩擦因数
齿轮涂层啮合齿面的摩擦因数与齿面粗糙度、涂层和润滑油黏度等密切相关。为准确获取不同厚度涂层的摩擦因数,在标准试件表面制备不同厚度的磷酸锰转化涂层,采用德国OPTIMOL公司生产的SRV微振动摩擦磨损试验机对不同膜厚的涂层标准试件进行摩擦因数测试。图2为在扫描电子显微镜下观察到的磷酸锰转化涂层的表面形貌。磷酸锰转化涂层表面存在少量的孔隙结构,使齿轮表面具备良好的储油润滑特性,通过控制反应颗粒度可获得不同厚度的磷酸锰转化涂层。

图2 不同厚度的磷酸锰转化涂层表面形貌
图3 为在200N垂直载荷作用下,两种厚度的磷酸锰转化涂层与未做涂层处理试件的摩擦因数(COF)随着时间的变化曲线。由图可知,随着时间的增加,摩擦因数略有下降,逐渐趋于平稳。在齿轮摩擦热流密度的计算中,选取平稳后的数值作为涂层齿轮的摩擦因数,测试结果为厚涂层摩擦因数f1=0.107,薄涂层摩擦因数f2=0.125,无涂层齿轮的摩擦因数 f3=0.132。
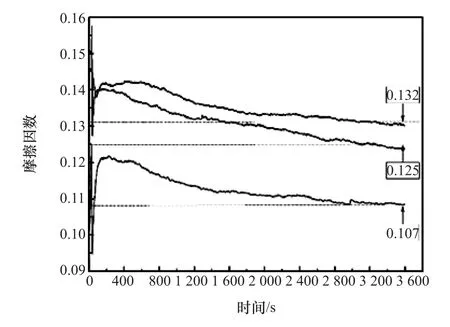
图3 不同厚度磷酸锰转化涂层摩擦因数曲线
2 对流换热系数
2.1 齿轮啮合面的对流换热系数
齿轮传动中,齿面上摩擦热能中的一部分由热传导进入齿轮齿体,另一部分则通过作用于啮合齿面上的润滑介质对流而冷却扩散[8]。齿轮传动中的对流传热是润滑介质(润滑油和空气介质)与齿轮之间的传热过程,主要依靠润滑介质的流体质点相对移动与混合而传热,因此对流换热系数与流体流动状况密切相关。自动变速器齿轮传动通常采用飞溅润滑,在瞬态和强制对流传热的条件下,建立不可压缩流体的能量方程,并将各变量单位化,即单位体积与时间内从齿面扩散的摩擦热量Qt可用间歇冷却过程中的标准化总冷却量qt[10]表示:
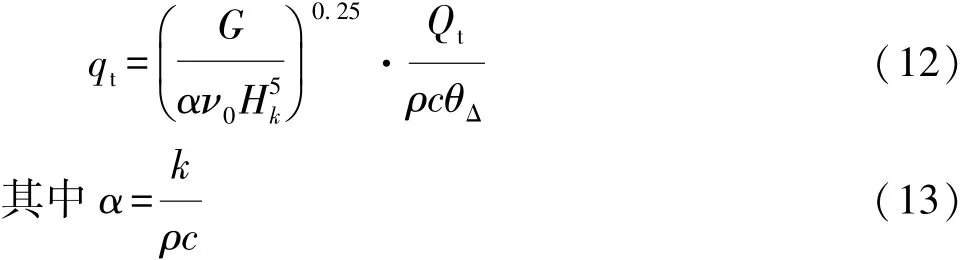

式中:G为齿轮的离心加速度,G=ω2ri,ω为齿轮的旋转角速度,ri为齿面上任意接触点的半径;ν0为润滑油在供油温度时的运动黏度;α为热扩散系数;k,ρ,c分别为润滑油的热传导率、密度和比热容;Hk为齿面上任意接触点半径所在处轮齿的高度;θΔ为齿面平均平衡温度与润滑油初始油温的差别常数。由总冷却量qt可以求出单位时间和体积内从轮齿啮合面扩散的摩擦热量Qt。
由式(12)~式(14)和关系式 G=ω2ri,可得
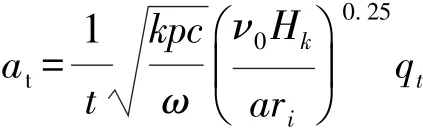
以齿轮旋转一周的时间计,t=2π/ω,则齿轮啮合面的对流传热系数为
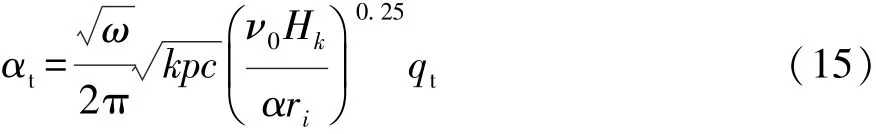
2.2 齿轮端面的对流换热系数
齿轮端面的对流换热分析可简化为旋转圆盘的对流换热分析,通过对润滑油雷诺数的分析,齿轮端面的润滑油流动为层流,故齿轮端面的对流换热系数为

式中:νf为润滑油运动黏度;m为指数常数,m取为2;K0为润滑油传热系数;Pr为普朗特数。齿轮其他面包括齿根面、齿顶面和非啮合面的对流换热系数尚未有统一的计算公式。为简化计算,直接将啮合齿面的对流换热系数经过修正作为非啮合齿面的对流换热系数[13]。
3 齿轮涂层-基体系统温度场仿真
3.1 相关参数
啮合齿轮的温度通常分本体温度和瞬时温度,而齿面的瞬时温度又取决于齿轮的本体温度[14]。在齿面滑动摩擦生热与润滑油强制对流冷却的共同作用下,轮齿本体温度经过一定周期旋转后可在固定载荷、转速和润滑条件下达到热平衡。在高速运转的热平衡状态下,热量由齿面向齿体传导时间非常短,且润滑介质带走了大部分的齿面摩擦热量,瞬态温度在一个旋转周期内的变化非常小。为此齿轮传动的温度一般考虑为稳态温度场[15]。在所选齿轮对啮合过程中,由于主动轮的转速较高,其齿面温度通常高于从动轮的齿面温度,为此选取主动轮为分析对象。齿轮相关设计参数如表1所示。

表1 齿轮基本参数
3.2 热物性参数
通过试验方法获取齿轮材料20MnGrS5在工作温度80℃下的热物性相关参数,如表2所示。
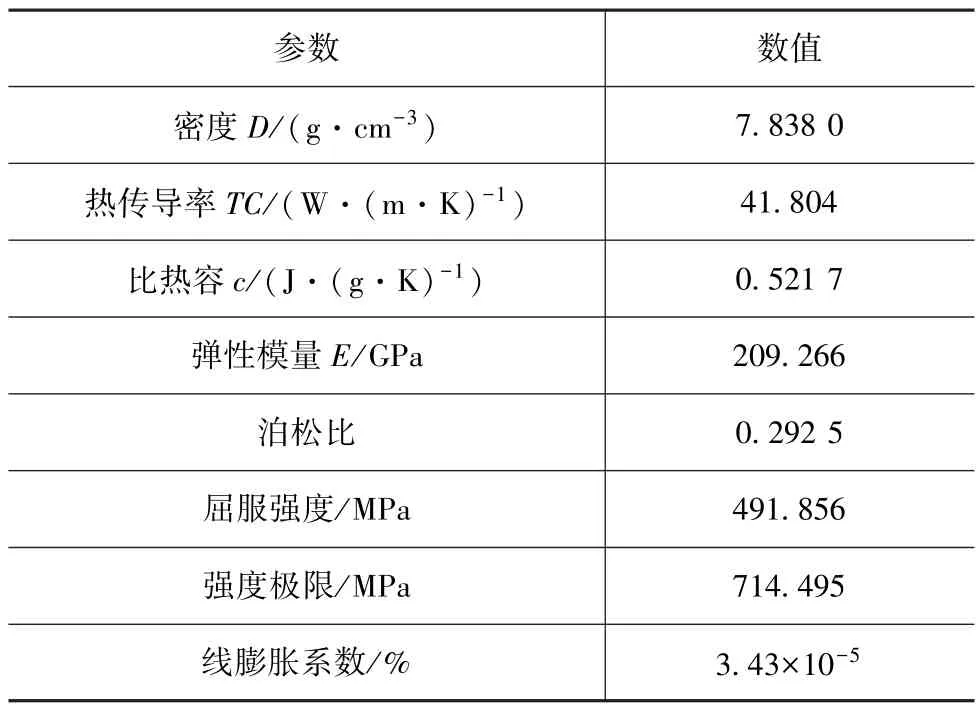
表2 齿轮材料参数
3.3 涂层齿轮有限元模型建立
图4为涂层处理后齿轮的单齿有限元模型。基于磷酸锰转化涂层的制备原理,应用概念建模法在齿轮表面分别建立10和15μm厚度的涂层模型。自动变速器的工作温度通常在80~120℃[1],计算时设定环境温度为80℃,同时在齿轮的非工作面与齿轮端面设定对流换热系数,在齿轮的工作面上设定摩擦热流密度。摩擦热流密度随着啮合点位置而变化,将计算所得的摩擦热流密度作为面载荷施加在齿轮工作面上。

图4 斜齿轮有限元网格与热流量边界
3.4 结果分析
图5 为求解获得的涂层处理前后齿轮稳态温度场的分布。由图可知,厚涂层齿面的最高温度为100.06℃,薄涂层的齿面最高温度为106.35℃,未经涂层处理的齿轮齿面温度为108.45℃。显然,涂层处理后齿轮的最高温度明显低于处理前的最高温度,且厚涂层齿轮本体温度在三者中最低,由于齿轮表面的转化涂层厚度均匀,且一致性良好,涂层处理对于齿轮的稳态温度场分布特点基本没有影响。
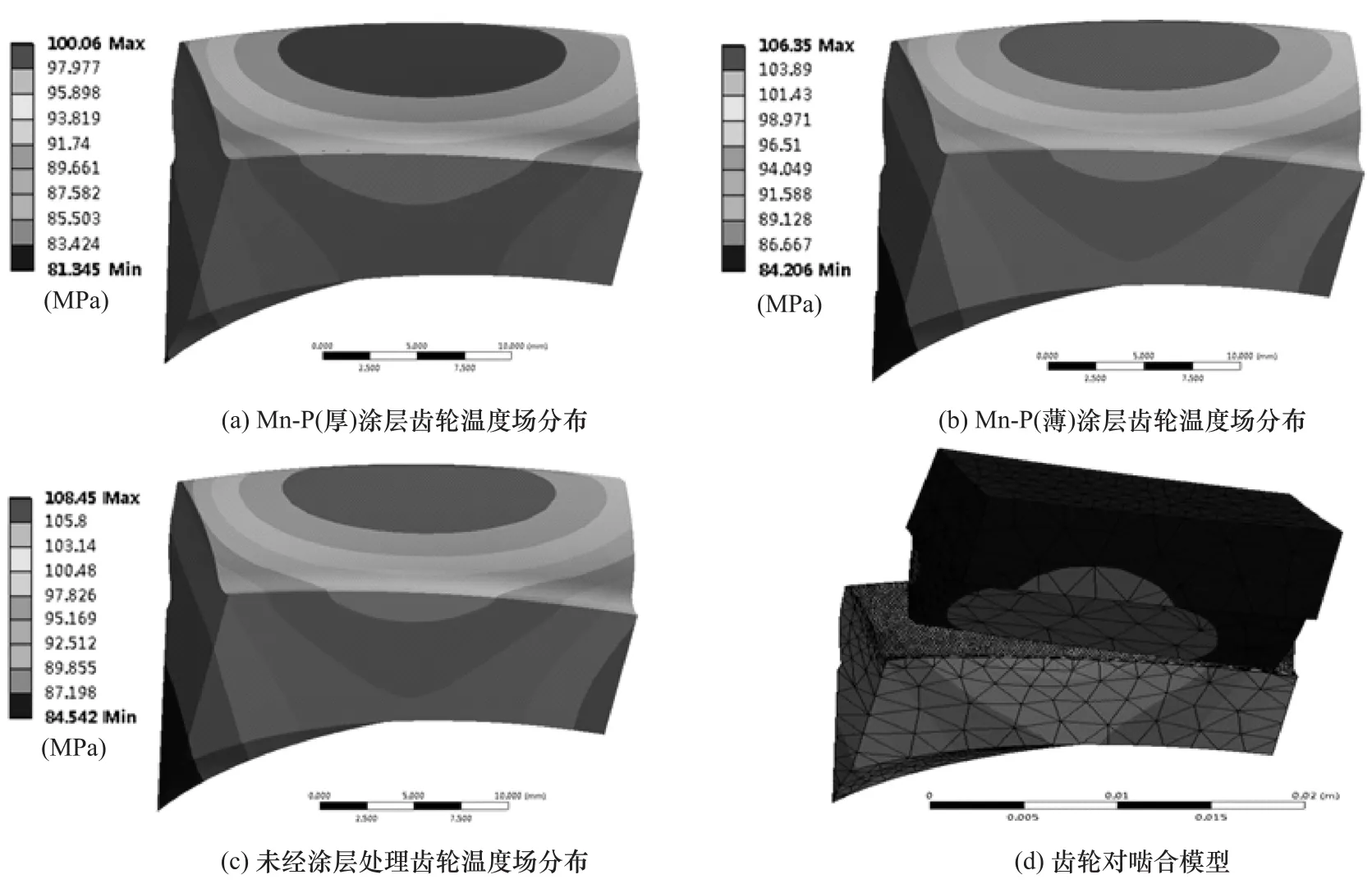
图5 环境温度80℃时涂层处理前后齿轮的稳态温度场分布
图6 为在恒定转速3 000r/min与恒定转矩300N·m工况下,两种厚度涂层与未经涂层处理的齿轮沿齿宽方向和沿齿高方向的温度对比。由图6可知,涂层齿轮的温度有明显降低,厚涂层齿轮表面温度下降更为明显,比未经涂层处理的齿宽方向最高温度下降约7%,齿高方向最高温度下降约8%。主要原因在于厚涂层表面具有更低的摩擦因数,使齿轮表面产生更少的摩擦热量[16]。
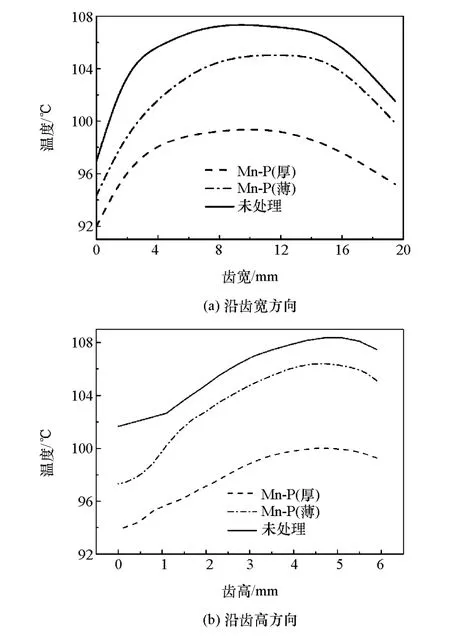
图6 涂层处理前后齿轮啮合面的温度分布
图7 (a)为齿轮输入转速恒定为3 000r/min时,输入转矩对齿轮最高温度的影响,图7(b)为齿轮输入转矩恒定为300N·m时,输入转速对齿轮最高温度的影响。由图可知,齿轮的最高温度随转速和转矩的增大而升高。齿轮本体温度随转矩和转速的增加温度增幅降低,厚涂层齿轮的这一趋势更为明显,对齿轮表面具有更好保护的效果。分析上述原因,转速和转矩的增加导致齿面各处摩擦热流量不同程度地增加,齿面各处本体温度不同幅度提高,随着转速和转矩的增大,抑制齿面温度上升的因素增加,使齿面各点温度的增加幅度减小[17]。同时,具有厚涂层的齿面摩擦因数更小,且颗粒度较大的厚涂层具有更好的散热效果,其齿轮本体温度也相对最低[18]。

图7 涂层处理齿轮最高温度随转速和转矩的变化规律
4 齿轮传动温度场台架试验
4.1 齿面温度测量方案
齿面温度测试试验在CN-GZ-132齿轮动力循环加载试验台上进行,试验齿轮采用喷油润滑方式,采用FLIR-T1040红外热成像仪对不同工况条件下的齿轮表面温度进行测试。图8示出待测齿轮箱和测试系统原理图。为便于对齿轮温度的测量,测量时通过控油阀将润滑油流量调至最低,降低润滑油对齿轮温度的影响,红外热成像仪测点布置在啮合齿轮对的正上方[18]。
为利用红外热成像仪对齿面进行精确测温,测试前对齿面发射率进行标定。齿轮试验机的工况条件如表3所示,齿轮箱油温控制在80℃,分别对未涂层处理齿轮和磷酸锰涂层(薄)齿轮对进行齿面温度测试,红外热成像仪距离待测齿面30cm,每种工况齿轮表面温度测试4次,读取最高温度并计算平均值。
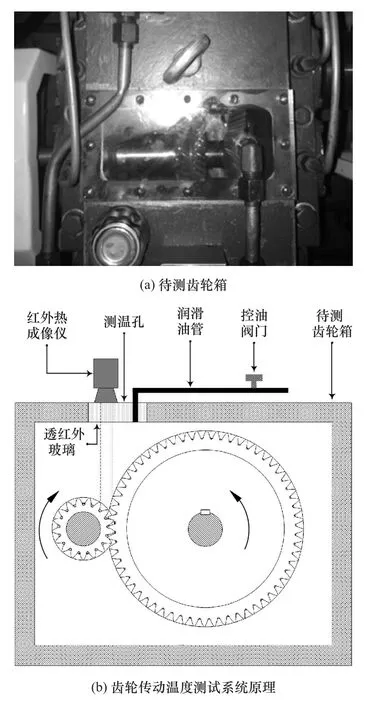
图8 齿轮传动温度测试系统

表3 齿面温度试验参数
4.2 齿面温度测量结果
图9(a)为2 000r/min和200N·m条件下的涂层齿轮温度场云图,最高温度为94.4℃,图9(b)为涂层处理前后齿轮温度测试结果对比。从图中可以看出,试验值较仿真值的齿面温度高,但温度上升趋势基本一致,试验结果验证了仿真得出的齿面温度随转速的升高和转矩加大而增高的规律。分析原因,推测是为便于温度测试,在红外热成像仪测试温度瞬间,降低了齿轮的喷油量,使齿面润滑油减少导致齿面温度上升,但计算结果和试验结果的误差范围在4%~7%之间,表明本文中所提出的确定涂层齿轮温度模拟方法是可行的。
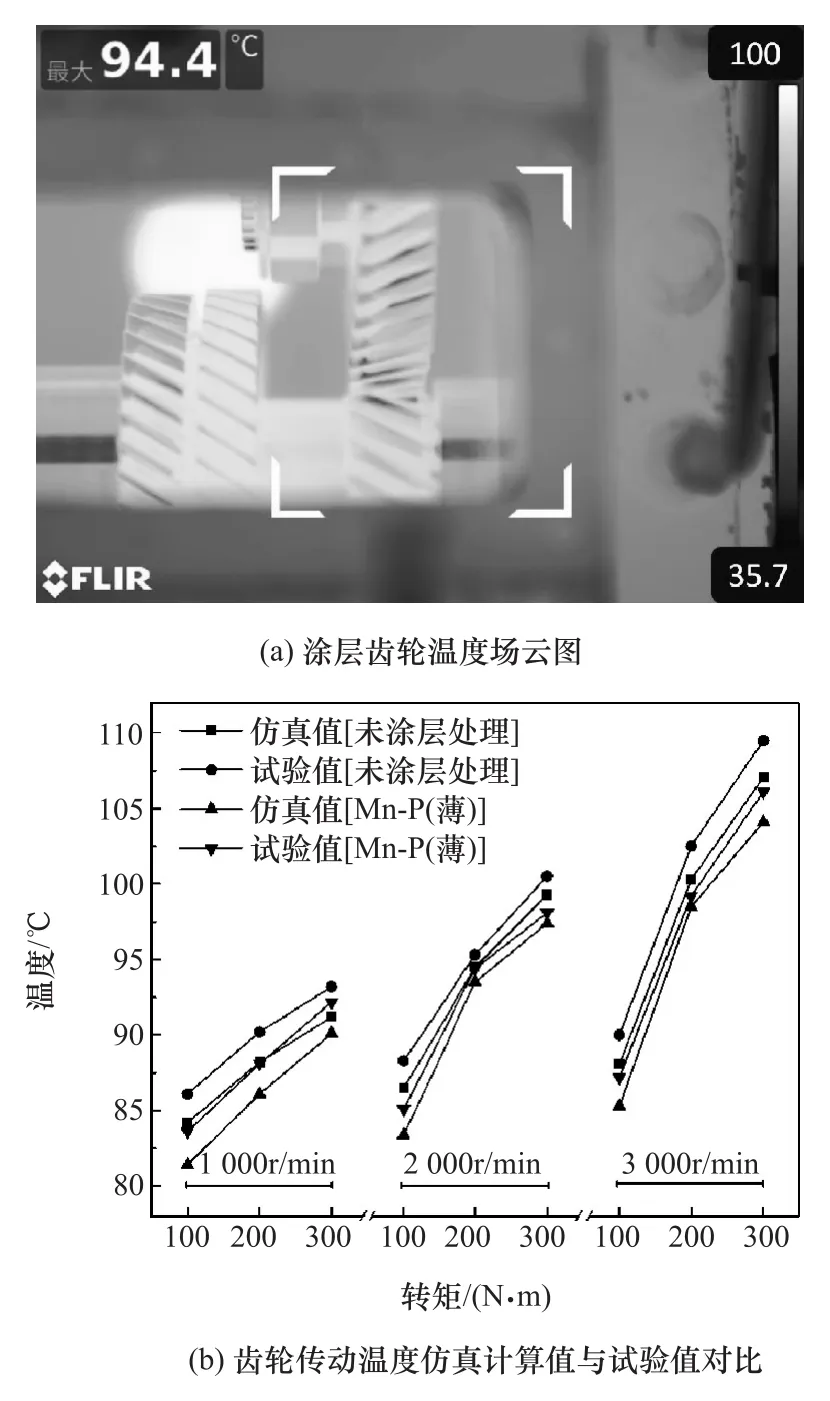
图9 齿轮传动温度场测试结果
5 结论
(1)磷酸锰转化涂层表面不规则多孔结构起到储存润滑油作用,利于油膜形成,有效降低了齿轮副表面的摩擦因数。通过摩擦试验表明,较厚的转化涂层具有更低的摩擦因数,进而使变速器齿轮具有更高的抗点蚀疲劳寿命。
(2)轮齿最高温度位于接触面中心偏向齿顶的位置,涂层处理后的齿轮最高温度明显低于未经涂层处理齿轮的最高温度。齿轮的最高温度与转矩、转速等负载条件呈正相关,随转矩、转速的提高而增高。
(3)通过对不同厚度的磷酸锰转化涂层齿轮啮合面沿齿宽和齿高方向的温度对比表明,不同厚度的涂层处理均可有效降低齿轮的啮合温度,且随着涂层厚度的增加齿轮表面摩擦温度降低,但对齿轮表面的稳态温度场分布影响不明显。
(4)采用红外热成像仪测温系统在齿轮传动试验台上对涂层处理前后的齿轮温度场进行了测量,测试结果验证了测试模型的准确性。
