复合材料简支梁发生一维贯穿型脱层后的振动变化分析
2018-10-13程澄
程澄
复合材料简支梁发生一维贯穿型脱层后的振动变化分析
程澄
(山东建筑大学机电工程学院,山东 济南 250101)
复合材料作为一种性能优异的新型材料,广泛应用在航天、化工、纺织、医学等领域。复合材料梁在生产和使用过程中极易产生脱层。脱层问题会引起梁结构的变化,从而对梁的振动产生较大的影响。利用ANSYS软件,建立复合材料简支梁的有限元模型,对复合材料简支梁在未发生脱层前以及发生一维贯穿型脱层之后的前10阶固有频率比较,得出了复合材料简支梁的脱层对频率的影响结果。
复合材料;简支梁;一维贯穿型脱层;频率
1 引言
近年来,随着国民经济总值的增加,基础设施越来越完善,而已有结构的维修与防护成为了新的问题。近年来,新兴的复合材料梁以其优异的性能,在工程应用中被广泛关注。复合材料因其在增加强度、减轻质量、耐腐蚀、抗疲劳等方面的优良特性,被广泛应用于航空航天、风力发电、汽车配件等各个领域。
梁作为现代工程的常用结构之一,在工程中随处可见。复合材料简支梁的主要破坏形式就是脱层。复合材料梁的脱层也分为很多种,从脱层区域的大小相对于层合结构而言,可以将脱层分为一维贯穿型分层模型、二维浅埋或深埋圆形和椭圆形脱层;从脱层处于层合结构厚度位置和脱层的数量,可以分为薄膜脱层、单层脱层、多重脱层。本次研究的是复合材料简支梁发生一维贯穿型脱层(薄膜式)之后对前10阶固有频率的影响。一维贯穿型脱层复合材料简支梁模型如图1所示。
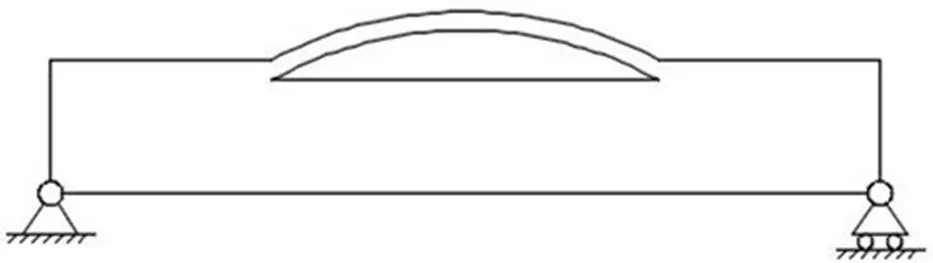
图1 一维贯穿型脱层复合材料简支梁模型
复合材料梁脱层之后由于其整体结构的变化,会引起固有频率的变化,因此研究其脱层之后和脱层之前频率的变化,有助于在复合材料梁发生脱层之后,对固有频率的变化得到一个预判值,从而避免发生共振。
2 脱层的复合材料简支梁模态分析的理论基础
脱层将复合材料简支梁分为4个次梁,脱层处假设为自由振动。分层梁情况如图2所示。
振动的控制方程为:
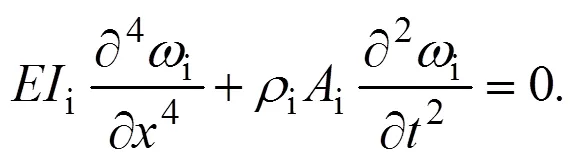
式(1)中:i为弯曲刚度;i为密度;i为横截面积。
该方程的通解为:
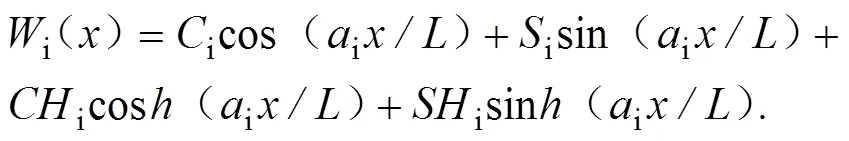
其中:
通解中共有14个未知系数,利用边界条件以及分层处的连续性条件,可解出未知系数。边界条件提供4个齐次方程,连续性条件提供10个齐次方程。
梁在=1和=4处的边界条件为:=0,〞=0.
分层处为自由振动模型,=2的连续性条件如图3所示。
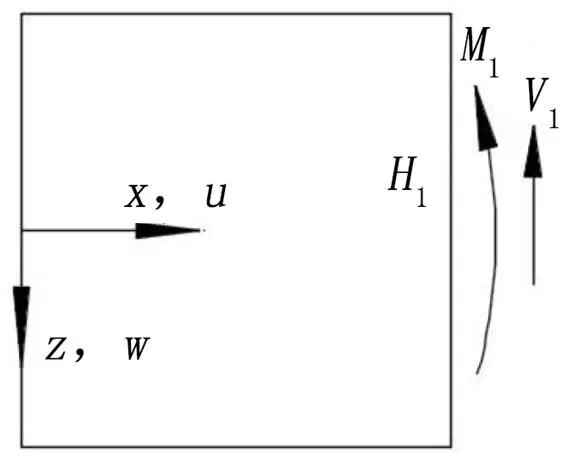
3 复合材料简支梁有限元模型的建立
本次研究的一维贯穿型脱层复合材料简支梁,由于模型比较简单,加之直接在有限元软件里进行建模可以避免很多问题,所以选择在有限元软件里直接进行建模,并划分多种网格进行比较,选择最优网格进行求解,最终获得脱层和未脱层的复合材料简支梁的前10阶固有频率。
由于简支梁模型比较简单而且主要研究的是,方向的振动变化情况,故选用2D模型,采用PLANE182四节点单元,通过设置实常数的方法控制简支梁的厚度。
复合材料梁的密度、各个方向上的泊松比和弹性模量数据见表1.
表1 材料属性
属性密度E11E12E33G12G13G23v12v13V23 数值1 718 kg/m336.80 GPa15.38 GPa3.3 GPa3.26 GPa1.03 GPa1.89 GPa0.400.300.32
采用自底向上建模的方法,以梁的最左端支座为坐标原点。对脱层的复合材料简支梁进行建模时,由于脱层的尺寸非常小,注意生成区域是否正确。
建模完成后划分网格。脱层的复合材料梁划分网格采用自由网格划分及三角形网格划分,比较网格质量,选用最优网格。自由网格划分完成之后,在多个地方出现三角形形状的网格,这种畸形网格会导致有限元求解中的病态方程,导致求解结果不够准确,脱层部分畸形严重。三角形网格划分之后,脱层部分网格划分得比较均匀,整体网格也比较均匀。对比网格质量选用三角形网格,将网格尺寸细化后,结果显示差别不大,网格无需进一步细化。边界条件为最左边的固定支座处为全约束,最右边的支座处为限制方向的移动。设置进行模态分析,并提取前10阶固有频率,不设置频率的提取范围,求解并查看后处理。
4 结果
经过有限元软件分析的未脱层的复合材料简支梁和脱层的复合材料简支梁前10阶固有频率见表2和表3,脱层的复合材料简支梁的模态振型从简支梁的整体弯曲转变为脱层部分的弯曲。
表2 未脱层的复合材料简支梁的前10阶固有频率
频率阶数12345 频率/Hz18.93653.60875.055121.44172.48 频率阶数678910 频率/Hz225.80253.63284.28346.41410.98
表3 脱层的复合材料简支梁的前10阶固有频率
频率阶数12345 频率/Hz18.68531.61349.68956.57370.951 频率阶数678910 频率/Hz111.72115.13161.59183.47213.90
5 结果分析及结论
脱层之后复合材料梁的一阶频率与脱层之前的差别不大,但是从第二阶固有频率开始,脱层之后的复合材料梁的固有频率大大降低,从第四阶固有频率开始,脱层之后的复合材料简支梁固有频率大约是脱层之前频率的1/2.振型也发生了很大的变化,脱层的复合材料简支梁的振型主要是脱层部分的弯曲。所以,当复合材料简支梁发生一维贯穿型脱层之后,我们可以获得前10阶固有频率的预判值和振型的变化,从而避免共振的发生,造成事故。
[1]李欣业,张明路.机械振动[M].第四版.北京:清华大学出版社,2009.
[2]蔡忠云.含脱层损伤复合材料层合梁动力特性的理论与实验研究[D].上海:上海交通大学,2009.
[3]Christian N.Della,Dongwei Shu.Free Vibration Analysis of Multiple Delaminated Beams under Axial Compressive Load[J].Journal of Reinforced Plastics And Composites,2009,28(11):1365-1381.
[4]刘湘龙.具脱层复合材料层合梁-板的自由振动分析[J].长沙理工大学学报(自然科学版),2014,11(4):60-64.
[5]杨金花.具脱层复合材料层合圆柱壳的非线性静动力学性能与脱层扩展研究[D].长沙:湖南大学,2006.
[6]S.Madhu,M.Kumaraswamy.Experimental Investigation and Free Vibration Analysis of Hybrid Laminated Composite Beam Using Finite Element Method[J].International Journal for Research in Applied Science& Engineering Technolilgy,2017(6):40-53.
〔编辑:严丽琴〕
2095-6835(2018)19-0086-02
TB33
A
10.15913/j.cnki.kjycx.2018.19.086
