2018年高考全国I卷统计概率问题的分析及备考建议

广东省东莞市东莞中学(523005) 庞进发

2018年高考结束,全国高考I卷理科数学第20题统计概率解答题(以下简称“试题”)就成为广东省,乃至全国议论的数学热点问题,对问题背景、设问形式以及解答等方面有不同的议论.然而2016年广东省进入全国卷以后,统计概率解答题的得分都不尽人意.并且2016年和2017年全国高考I卷理科数学卷把统计概率解答题排在第19题位置,今年甚至排在第20题位置,相当于次压轴题.据了解,广大数学教师对于统计概率解答题复习备考也在不断地探讨,但收效甚微.究其原因,初中、高中关于统计概率的教学更多的停留在表面的套用公式计算上,缺乏对统计概率背景的了解,过程的经历、体验和感受少,知识本质的挖掘不透彻,对统计思维、随机思想的培养不够;高三复习备考时,受2016年以前统计概率试题的思维影响,重套公式计算,缺乏对题目背景的分析、概率模型的构建和统计意义的理解,并且没有找到较多合适的训练素材.本文以数学核心素养,从教育价值的的视角对“试题”进行分析与提出备考建议.

试题(2018年全国高考I卷理科数学第20题)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品,检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为p(0＜p＜1),且各件产品是否为不合格品相互独立.

(1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0.

(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.

(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX;

(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?

1.近三年全国I卷理科数学试题的比较

通过比较发现,近三年问题背景都是工业生产的抽样检验决策问题,2018年“试题”问题背景为产品是否合格抽样检验,广大考生更加熟悉.统计概率问题作为应用性问题,题目的字符数都比较多,重点考查了考生通过阅读,整理数据、提取信息、构建模型、进行推断、获得结论的数据分析过程与能力,同时考查了数学运算能力.2018年“试题”有关次函数的最值点的求解,难度更大一些.

2.解法研究

2.1 问题分析

统计概率问题阅读量比较大,那么如何在题目中提取有用的信息以及对数据的整理,非常关键,也是解决问题的切入点.如“试题”中通过“先从这箱产品中任取20件作检验”和“设每件产品为不合格品的概率都为p(0＜p＜1),且各件产品是否为不合格品相互独立.”两个信息,考生要联想到相应的知识—n次独立重复试验.而第(1)问中“记20件产品中恰有2件不合格品的概率为f(p)”,考生要联想到n次独立重复试验恰有k次发生的概率计算方法与公式:“试题”中考生感觉比较陌生的是以概率p为自变量的函数f(p)形式,不能把f(p)与进行对应:导致不能正确找到问题解决的切入点.还有第(1)问要求函数最大值点p0,对于大多数考生也是难点,因为考纲的要求是考生会求“不超过三次的多项式函数的最大值、最小值”.但这里是求最大值点p0,运用教材中给出的基本初等函数的导数公式和导数的四则运算法则以及单调性的判定方法即可求解,考查了考生思维的灵活性.

第(2)问解决的关键是对“试题”中的信息“如检验出不合格品,则更换为合格品”和“已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.”的联系理解.也就是说如果检验,就没有不合格品进入用户手中,工厂只需要付每件产品的检验费用2元即可;如果不检验,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.考查了考生对信息的重新整合理解能力.还有对“试题”中“现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0作为p的值”这个信息的处理,应分拆开理解与应用.“现对一箱产品检验了20件,结果恰有2件不合格品”是表示已经检验的20件产品,工厂只需付检验费20×2=40元,因为2件不合格品已经更换为合格品,没有不合格品进入用户手中.“以(1)中确定的p0作为p的值”是应用在剩下的180件产品如果没有检验,估计其不合格品的件数,而这些不合格品进入用户手中,工厂需要支付赔偿费,没有检验费.评卷过程中发现,很多考生把以上两个方面混在一起,直接把p的值等于而正确的理解是p=p0=0.1.

2.2 教育价值分析

“试题”重点对考生的数据分析核心素养的考查,考查了考生对统计概率基本概念的理解掌握,如n次独立重复试验、n次独立重复试验恰有k次发生的概率计算公式、二项分布及其数学期望的计算.“试题”特别考查了考生对信息处理能力,如何通过阅读,获取与整合有关统计信息,如把“试题”中的信息“如检验出不合格品,则更换为合格品”和“已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.”进行整合,找到问题解决的突破口.“试题”还考查了考生概率分布模型的构建,把不服从二项分布的随机变量X转化为服从二项分布的随机变量Y,并且应用数学期望的线性关系求随机变量X期望值.除此之外,“试题”对于运算综合能力也作了考查,如超过三次的多项式函数的求导,求最大值点.还有“试题”最后一问对统计决策思维考查,考查考生通过数据分析进行推断的能力,“以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验”,即要从两个方面计算.一方面是:如果对这箱余下的所有产品不作检验,则由前一问已经算出检验费用与赔偿费用和的期望值为490元;另一方面是:如果对这箱余下的所有产品作检验,则只需付检验费用400元,检验费用与赔偿费用和的期望值为400元.然后比较两种情况的期望值,即可下结论:应该对余下的所有产品作检验.

2.3 解法剖析

2.3.1 第一问主要是根据n次独立重复试验恰有k次发生的概率计算公式列出有关p的函数f(p),然后再求最大值点.详细解答如下:

解法一(1)20件产品中恰有2件不合格的概率为因此

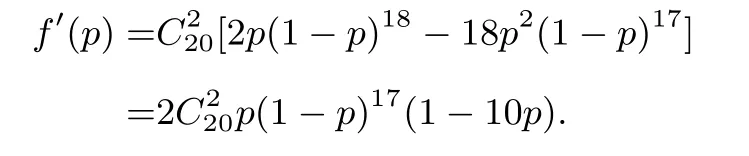
令f′(p)=0,得p=0.1.当p∈(0,0.1)时,f′(p)＞0;当p∈(0.1,1)时,f′(p)＜0.所以f(p)的最大值点为p0=0.1.

评析有很多考生不能正确写成f(p)解析式,其原因是对n次独立重复试验恰有k次发生的概率计算公式不熟悉.能正确写成f(p)解析式的考生,又有大部分不会求最大值点,或者求导出错、求最大值点时没有说明单调性,表达不严谨等.

“试题”的最大值点p0=0.1,恰好等于也可以推广到一般的情况:

记n件产品中恰有k(0≤k≤n)件不合格品的概率为f(p),则f(p)的最大值点

实际上,n件产品中恰有k(0≤k≤n)件不合格品的概率为因此,令f′(p)=0,得当时,f′(p)＞0;当时,f′(p)＜0.所以f(p)的最大值点为

解法二(1)20件产品中恰有2件不合格的概率为

因为0＜p＜1.所以当且仅当9p=1-p即时,等号成立,即f(p)取得最大值.所以f(p)的最大值点

评析很少考生能正确应用基本不等式求f(p)的最大值点p0,基本不等式的拆项对考生能力要求较高.

2.3.2 第二问主要是在第一问的基础上,应用二项分布期望值求解公式求出检验费用与赔偿费用和的期望值,并进行决策判断.详细解答如下:

(2)由(1)知,p=0.1.

解法一令Y表示余下的180件产品中的不合格品件数,依题意知Y～B(180,0.1).X=20×2+25Y即X=40+25Y,所以EX=E(40+25Y)=40+25EY=490(元).

评析随机变量X表示“这一箱产品的检验费用与赔偿费用的和”,不服从二项分布,而另外假设随机变量Y表示“余下的180件产品中的不合格品件数”,服从二项分布,再建立起随机变量X与Y的关系X=20×2+25Y,应用数学期望的线性关系公式进行求解,考查了考生转化的能力以及概率模型意识.有部分考试直接写出X的数学期望:没有应用二项分布,直接应用样本估计总体或几何分布求解,依据不充分,思维不严谨.

解法二(I)设检验费用为X1元,赔偿费用为X2元,若不对该箱余下的产品作检验,则检验费用为X1=20×2=40(元).因为已经检验了20件,还剩下180件没有检验,设180件产品中有不合格产品n件,由(1)得即所以,E(X2)=18×25=450(元).所以,E(X)=450+40=490(元).

评析检验费用和赔偿费用分别计算其数学期望,再进行求和.

解法三(i)X的可能取值为40,65,90,···,4540.

评析直接列出随机变量X的所有可能取值,求出其分布列,然后再算出数学期望值,这方法理论上可以算出答案,但计算量非常大,极个别考生能够正确表达,有些考生只能列出X的可能取值为40,65,90,···,4540.很多考生都是错误地列出X的可能取值为40,65,90,原因是把剩下的180件产品理解为20件产品中不合格产品可能有0,1,2件,关系上混淆.

解法四 (i)设检验费用为X1元,赔偿费用为X2元,每一件产品赔偿费用为ξ元.若不对该箱余下的产品作检验,则检验费用为X1=20×2=40(元).因为每件产品不合格的概率为0.1,若有不合格品进入用户手中,赔偿费为25元.所以

所以Eξ=0×0.9+25×0.1=2.5.所以EX2=180×2.5=450(元).E(X)=450+40=490(元).

评析在计算赔偿费用时,先计算每件产品赔偿费用的数学期望值,再计算剩下180件产品的赔偿费用的数学期望值.

(ii)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元.由于EX＞400,故应该对余下的所有产品作检验.

3.备考建议

3.1 以实例为载体,理解统计概率基本概念教学中应通过对一些典型案例的处理,使学生经历较为系统的数据处理全过程,在此过程中学习数据分析的方法,理解数据分析的思路,运用所学知识和方法解决实际问题.因此,在高考复习中,统计概率的复习也要结合具体的实例,通过课本中的例题、习题,让学生深刻地理解统计概率的基本概念.例如对于条件概率的理解,就可以通过教材中的实例“三张奖券中只有一张能中奖,现分别由三名同学无放回地抽取,如果已经知道第一名同学没有抽到中奖奖券,那么最后一名同学抽到中奖奖券的概率是多少?”,让学生从不同角度的运算,反复地理解条件概率以及运算.

3.2 加强阅读与信息处理能力培养

阅读与信息处理能力考查是近三年全国I卷理科数学统计概率解答题的突出特点,有文字阅读,也有数学图表的阅读.如2016年全国I卷理科数学统计概率解答题就涉及到柱状图以及文字的理解,通过柱状图获取到以这100台机器更换的易损零件数的频率代替1台机器三年内需更换的易损零件数发生的概率信息,可以得出1台机器更换零件数为8,9,10,11的频率分别为:0.2,0.4,0.2,0.2,从而得出2台机器三年内共需更换的易损零件数X的所有可能取值为16,17,18,19,20,21,22,然后再求出X的分布列.复习备考时可以结合典型的例子,给学生充分的时间,引导学生阅读,通过阅读后,让学生表述,提升信息处理的基本能力.

3.3 注重渗透模型化思想

高考中统计与概率的问题基本上是应用问题,情景的设置贴近学生的生活实际,对数学建模都有一定的要求.特别是理科试卷集中在离散型随机变量的分布列、离散型随机变量的期望值和方差等.例如,要求学生能够识别题中提出的随机变量服从什么分布,并应用相应公式,求出其分布列.如2017年试题是通过“根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(µ,σ2).”和“假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(µ-3σ,µ+3σ)之外的零件数”判断随机变量X服从二项分布.所以在复习备考时需要引导学生分析,试题给出多少个随机变量.如果是一个随机变量,先判断其是否服从两点分布、二项分布或超几何分布,或者一般的分布;如果是两个随机变量,要判断是研究线性相关问题还是独立性检验问题,从而强化学生的模型意识.

3.4 突出统计思维培养

统计思维是一种重要的思维方式,它和确定性思维一样成为人们不可缺少的思想武器,由不确定的数据进行推理也是同样有力而普遍的方法.统计的基本思维模式是归纳,它的特征之一是通过部分的数据来推测全体数据的性质.因此,统计结果具有随机性,统计推断是有可能犯错误的,这点与确定性思维不同.近三年高考试题对统计思维都有考查,2016年试题是“以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?”,2017年试题是“(I)试说明上述监控生产过程方法的合理性;”与“用样本平均数作为µ的估计值,用样本标准差s作为σ的估计值,利用估计值判断是否需对当天的生产过程进行检查?”.因此在复习备考中,特别要引导学生应用统计的思维来决策,一方面要有数据作为依据,另一方面要体现推断的随机性,如“估计”等.

3.5 强化运算综合能力

运算综合能力是解决统计概率问题必不可少的能力,并且高考对运算综合能力考查要求都比较高,在复习备考中要有足够的重视.一方面要引导学生学会相应的运算方法,另一方面要培养学生独立运算能力,让学生经历运算的全过程.如2017年试题中“剔除之外的数据,用剩下的数据估计µ和σ(精确到0.01)”,运算方法要求比较灵活,运算量也比较大.