直升机主减反共振隔振系统中附加阻尼器的影响分析

熊峰，王轲

（南京航空航天大学 振动工程研究所，南京 210016）

直升机和固定翼飞机相比，高效便捷，且具有优异的低速性能和悬停功能。因此在进行抗震抢险、救灾消防和处理紧急事故等方面十分迅捷[1]。直升机桨叶的结构和特性使它产生周期性的激振力，因此引起机身结构的振动。目前，直升机主减隔振方式主要有非聚焦隔振、聚焦隔振、节点梁隔振与动力反共振隔振等四种[2]。动力反共振隔振器是在由弹性元件与阻尼元件组成的常规隔振器的基础上附加由刚性杆与配重组成的惯性元件构成的隔振系统。在有力激励的条件下，某个特定的频率上，由惯性元件运动产生的惯性力完全抵消弹性力向基础的传递；在有运动激励的条件下，也可以把弹性力向隔振对象的传递全部抵消，因此在无阻尼的情况下隔振效果能达到传递率为零，随着阻尼的增加，传递率增大[3]。

国内关于动力反共振隔振器的研究也有不少。顾仲权等人提出了一种结合动力反共振隔振装置和主动力发生器的主动反共振隔振装置。从理论上说明了动力反共振隔振装置加入主动振动控制后隔振性能的改善情况，提出了一种主动控制参数的方法。这种方法考虑了控制力的限制和稳定性要求[4-7]。结果表明，采用主动控制能使动力反共振隔振装置的稳定性和传递率特性更好，尤其适用于同时存在随机激励和周期激励的条件。

阻尼器能有效阻碍物体的相对运动、并把运动能量转化为热能或其他可以耗散能量。工程中广泛使用的油液、空气阻尼器都可看做黏性阻尼器，提供与运动速度大小正比的阻尼力。在直升机主减试验件的共振梁上安装黏性阻尼器，一方面可以在全频带上抑制结构的振动，另一方面则对反共振隔振效率产生影响。文中试用仿真方法对阻尼的影响加以研究，为工程设计改进打下基础。

1 几种常见的粘滞阻尼模型

近百年来，学者们提出了诸多阻尼模型用于描述结构的阻尼矩阵，其中应用最广泛的阻尼模型是黏滞阻尼模型。黏性阻尼模型分为两类：比例阻尼模型和非比例阻尼模型。

1.1 Rayleigh阻尼模型

Rayleigh阻尼模型是比例阻尼模型中的一种。1877年Rayleigh将线性阻尼的观点引入了弹性体的振动方程。Rayleigh认为系统的阻尼矩阵是质量矩阵和刚度矩阵的线性组合，因此Rayleigh阻尼模型的特点是结构矩阵可以被结构固有振型解耦。用数学表达式可表示为：

式中：C 为系统的阻尼矩阵；M 为系统的质量矩阵；K表示系统的刚度矩阵；α和β则是阻尼系数，该系数可以通过任意已知的两阶阻尼比来确定，即：

式中：ωi是第i阶频率，ξi是第i阶阻尼比。

1.2 复阻尼模型

结构振动过程中，由于内部产生交变的应变，通过材料内摩擦而消耗内能。这种阻尼称为结构阻尼，一般用复数形式表示结构阻尼，亦称为复阻尼力，即：

式中：γ表示负阻尼系数。

1.3 Liang阻尼模型

虽然比例阻尼模型可以用系统固有振型将其解耦，使得原动力学系统方程变成线性方程组，但实际情况来说，往往都是非线性的复数形式。在试验测试过程中，所测试模态和频响也都是复数形式，我们所得到实模态信息也都是从复模态过程提取的。基于这样的原因，前面所提到的比例阻尼模型并不能更准确地模拟实际情况，所以一些学者提出了非比例阻尼模型。Liang阻尼模型是非线性阻尼模型中形式最简单，被应用最广泛的阻尼模型。1992年，美国国家地震中心的Liang博士和Lee教授针对实际结构和测试中往往都是复模态的情况，提出一种非比例阻尼模型。用数学表达式表示为：

式中：R为对角矩阵。与前面两类阻尼模型不同，Liang 阻尼模型并不能使用系统的固有振型矩阵将其对角化，即动力学系统不能解耦。因此这种阻尼模型只能在条件完备的情况下，通过动刚度矩阵求逆的方法求解频响。因此Liang阻尼属于非比例阻尼模型。

2 结构与模型

根据3D实体模型，对直升机主减隔振系统建立有限元模型，其中建模平台是采用 Hypermesh 10.0及Patran 2011。使用Msc.Patran软件建立的整体有限元模型如图1所示。有限元模型的尺寸和实体模型的尺寸是按1:1比例设计的。在模型中，以主减底部的中心为原点，向右为X轴正方向，向上为Z轴正方向，向前为Y轴正方向。

2.1 有限元模型单元设定

0D单元：模型中的0D单元主要是Point单元，用来表示质量块。为了表达质量块的移动，Point单元在每个位置上都有表示，但是每次计算时只有4个设置了属性，存在实际意义。

1D 单元：模型中的1D单元主要为Beam单元，用来表示支撑杆、螺栓等结构。其中螺栓结构由1～2个Beam单元表示，而每根撑杆由25个Beam单元表示。

2D单元：模型中的2D单元主要为Quad单元，用来表示薄板、连接处的耳片等和厚度远小于长宽的梁结构。

3D单元：模型中的3D单元主要为Wedge和Hex单元，用来表示长宽高相近情况下的固体部分。

2.2 约束条件设定

撑杆与顶部的连接：此处由两根短梁模拟螺栓通过轴承来连接撑杆。即模拟铰接连接，连接处是可绕短梁自身的Rx1方向自由旋转的。因此在撑杆上方第一个单元的第一个节点上放开了Rx1自由度，以实现自由旋转。

撑杆与支座的连接：与撑杆和顶部的连接相同，在撑杆下方第一个单元的第一个节点上放开了 Rx1自由度，以实现自由旋转。

柔性梁与主减主体的连接：此处由两根短梁模拟螺栓通过轴承来连接柔性梁和主体下方连接件的耳片。因此在两根短梁中间的节点上放开了 Rx1自由度，以实现自由旋转。

模组与共振梁的连接：每一个模组与共振梁间通过6根短梁模拟螺栓连接，短梁与模组和共振梁通过共节点固连在一起。

边界约束条件：支座约束。由于文中研究的主要是Z向受力和响应总和，为了便于查看计算结果，因此将4个支座的底面全部用多点约束MPC中的RB2单元连接到一点，将这一点进行6个自由度的位移约束，模拟将4个支座底面固连在机身上。

3 原结构动力学特性分析

在不安装阻尼器情况下，设置结构阻尼为0.01。利用 patran软件对直升机主减速器反共振隔振试验装置进行模态分析，模态分析得出前五阶固有频率见表1。

表1 模态分析

对最顶端的受力点沿Z方向施加1000 N的力，分析频率范围从 15～30 Hz，分析激励力与机体反力之间的数量传递关系，得到传递函数曲线如图2所示。

由图 2可见，在关心的频率范围内，有一个共振区和一个反共振区。共振峰值频率为24.6 Hz，载荷放大系数为9.8，反共振点的频率为25.6 Hz，对应反力为166.9 N。即最佳隔振率为84%，如要求隔振效率达到50%以上，则反共振有效频率范围为25.4～26.4 Hz。

4 附加阻尼器结构动力学特性分析

试件的一阶模态如图3所示，可以看出，试验件模型在端点处的振动幅度最大，速度最大，所以选择在试验件共振梁的四个端点上分别安装阻尼器。通过patran中properties 1D中的damper单元建立阻尼器模型，下端与梁端点相连，上端固定，模型如图4所示，一阶振型如图 5所示。图 6为阻尼系数大小为0.005和0.03时的传递函数曲线，与原频响函数曲线相比更为平缓，峰值明显降低。

调节阻尼系数大小分别为0.001，0.003，0.005，0.01，0.03，利用patran进行仿真计算得到的结果与原试验件比对结果见表2。将表2数据绘制成图线，如图7—10所示，可以看出，随着阻尼系数的增大，共振峰值逐渐降低，反共振点频率基本不变，隔振效率有所下降，有效隔振效率范围有所拓宽。综合考虑隔振效率与范围，建议将阻尼系数设置在0.01附近，不仅能有效地拓宽反共振隔振频率范围，还有更好的减振效率。

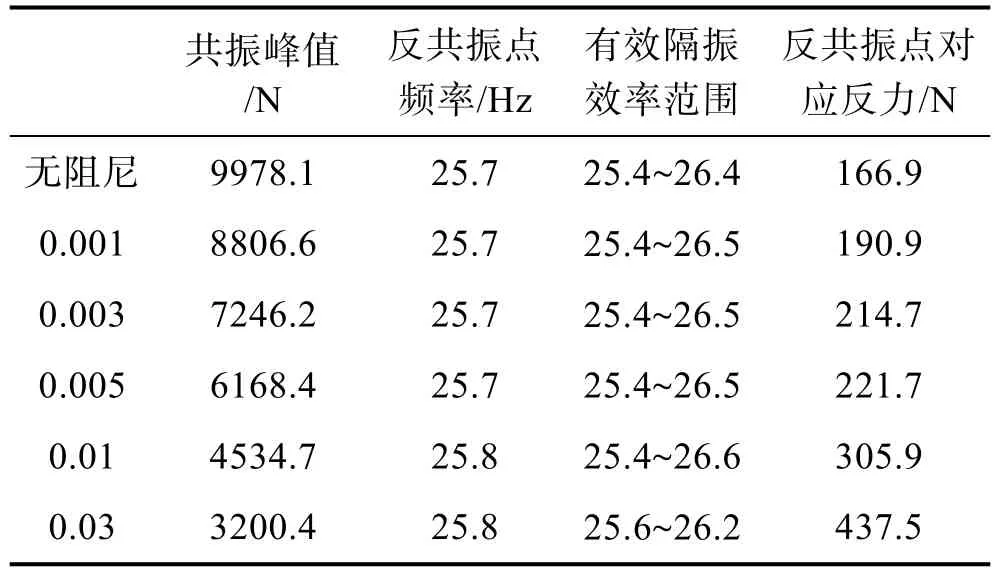
表2 实验结果

5 结语

文中采用仿真方法研究了附加阻尼器对直升机主减反共振隔振安装的影响。通过比较不同阻尼参数下的载荷传递规律，表明合理附加阻尼器，能有效拓宽反共振隔振频率范围，同时控制隔振传递率。