基于扫描式激光多普勒测振仪的叶片工作变形研究

杭超，燕群，黄文超

（中国飞机强度研究所 发动机强度研究室，西安 710065）

叶片是航空发动机的关键部件，由于高速旋转、数量多、以及载荷、工况复杂，使其成为发动机使用中故障率最高的零部件之一。由发动机叶片共振引起的叶片失效是设计人员关心的重要问题，为了保证叶片的可靠性，需要对发动机叶片进行模态分析，得到叶片在工作状态下的固有频率和振型，进而优化叶片结构，从而避免或减弱叶片在实际工作中可能会出现的共振[1]。

目前采用有限元和试验两种方法分别在叶片的设计阶段和验证阶段进行模态分析。在设计阶段，建立叶片的三维数字模型，用有限元方法计算叶片的固有频率和振型，根据计算结果调整叶片设计参数，使叶片满足设计频率的要求[2-3]。在验证阶段，对生产的叶片进行试验模态分析，测量叶片的前几阶模态参数，验证叶片的固有频率是否满足设计要求[4]。

目前常用激振器激励法和力锤激励法进行结构的试验模态分析（Experimental Modal Analysis, EMA），一般采用基于纯模态试验的相位共振法和基于频响函数矩阵参数识别的相位分离法，这些试验方法被广泛应用于结构模态分析中[5-6]。1987年 Dossing O[7]提出了工作变形（Operational Deflection Shape，ODS）的概念，用于评估机械结构动态性能。1997年Richardson M H[8]从模态分析理论和测试方面详细介绍了工作变形与模态振型的区别和联系，使得 ODS分析方法在未知激励的条件下得到了广泛应用。Kromulski J等[9]采用ODS方法分析了玉米分离器的工作变形，并用系统分析方法对ODS结果进行验证，两种方法测得的结果一致较好，证明了ODS的正确性。王学林等[10]采用ODS方法分析了风机叶轮的动态特性，测得了叶轮的振动峰值频率分布及其相应振型，并与锤击测试结果进行对比，验证了ODS方法的正确性，而且ODS方法识别重根模态具有优势。

文中选取某发动机叶片为研究对象，借助扫描式激光多普勒测振仪多点、非接触、高精度测量的优点，搭建叶片工作变形测试分析平台。用ODS方法分析叶片的前6阶固有频率及振型。最后计算不同阶次振型之间的模态置信准则，证明了工作变形分析结果的可靠性。

1 工作变形分析理论

振动模态是弹性结构固有、整体的特性。模态分析将结构的复杂振动分解为许多简单而独立的振动，并用一系列模态参数来表征。工作变形是指结构在指定频率下的变形，更为广义的工作变形是指结构上两点或多点在工作状态下的受迫运动。结构在工作状态下，仅通过测量结构上多个点的响应信号就能得到结构的工作变形。工作变形中包含了结构动态性能参数。工作变形分析经常用于激励载荷未知情况下的结构模态参数识别。

用工作变形分析结构模态参数的基本思路是：结构在工作状态下，测量结构上多个点的响应信号，计算工作变形频响函数（FODSFRF）。因为在共振频率处工作变形只被一个模态主导，所以可以认为该频率下的工作变形就是模态振型。通过在FODSFRF上选取共振峰，将所有响应点在共振峰频率处对应的振幅和相位组合在一起，就得到该共振频率下对应的振型。

结构上每个点响应与频响函数、激励都存在如下关系：

式中：Fy(jω)为响应信号的傅氏谱；Hy,fi(jω)为响应与激励之间的频响函数；Ffi(jω)为激励信号的傅氏谱。

如果结构的各阶振型对y点处的影响很小，则y点的系统集总频响函数也会较小，所以y点响应主要受环境激励的影响，可以近似表示为：

式中C为常数。因此，可以用y点响应信号代替激励信号计算FODSFRF。如果结构受到的外激力可测，则选取外激力信号作为参考信号；如果作用在结构上的外激力未知，选取受各阶振型影响较小的点的响应信号作为参考信号。将其他测点的响应信号作为流动信号，分别计算每个流动响应信号与参考信号的比值得到FODSFRF。实际应用时为了减小不相关噪声的误差，同时保留正确的相位信息，通常采用自功率谱和互功率谱计算FODSFRF，其数学表达式为：

式中：x表示流动信号；y表示参考信号；Gxy(ω)表示流动信号与参考信号的互功率谱；Gyy(ω)表示参考信号的自功率谱。

由以上分析可知，FODSFRF中包含了结构动态性能参数，且与结构频响函数形式类似。因此，可以通过在FODSFRF上选取共振峰来确定结构的固有频率，在该频率处对应的工作变形就是结构振型，振型的相位是响应点相对于参考点的相位。与传统试验模态分析方法相比，ODS方法不需要测量外激力，也不用进行频响函数拟合，测试分析过程简便，实时性好。但ODS方法只能得到频率和振型，不能得到阻尼比。

2 叶片工作变形试验

选取某发动机叶片作为研究对象，采用工作变形分析方法对其动态特性进行研究，分析叶片在10 000 Hz频率范围内的模态频率和振型。

2.1 试验系统

采用高频振动台作为激励设备，使用的恒幅正弦快速扫频激励满足工作变形分析的激励要求。为了高精度地测量叶片表面的运动，同时不给叶片附加质量，采用了扫描式多普勒激光测振仪采集叶片振动响应。激光测振仪是以多普勒原理为依据，可以直接测得结构表面的振动速度。扫描式激光多普勒测振仪多点、非接触、高精度测量的优点，非常适用于结构的模态分析。该激光测振仪的测试频率范围为80 kHz，最大速度量程为5 m/s。试验中激光测振仪的采样频率为25.6 kHz。

叶片工作变形试验的原理如图 1所示。可以看出，通过信号发生器发出快速正弦扫频电压信号（也称Chrip信号），激励振动台产生快速正弦扫频振动，同时用激光测振仪测量叶片表面一个点的速度信号，并用Chrip信号触发数据采集仪同时采集Chrip电压信号和测点的速度信号，对每个测点均重复采用上述方法测量。因为Chirp信号可以代表振动台的激励，工作变形分析方法是在FODSFRF上选取峰值，从而确定得到模态频率和振型。

2.2 试验步骤

叶片工作变形试验的步骤为：将叶片通过夹具安装在振动台上，并按图1所示连接试验设备；用扫描式激光测振仪在叶片表面布置55个测点，如图2所示；振动台产生一次Chirp振动激励，同时用激光测振仪测量叶片上一个点的振动速度信号，数据采集仪同步采集 Chirp信号和叶片上的速度信号，以 Chirp信号作为参考信号，按式（3）计算该测点的FODSFRF；激光测振仪换下一个测点，重复上一个步骤，直至所有测点完成测量；将Chirp信号作为参考信号，计算每个测点的FODSFRF，在FODSFRF上选取峰值，进行工作变形分析，得出叶片的固有频率和振型。

3 试验结果分析与讨论

在叶片工作变形试验中，选取Chirp信号作为参考信号，计算出每个测点的FODSFRF，由于测点数量多，为了曲线显示清晰，且不失一般性，图3给出了所有测点FODSFRF之和的幅值和虚部曲线。从FODSFRF曲线上寻找固有频率时，选取峰值尖锐且幅值和虚部都为峰值的频率点，作为叶片的固有频率，并提取峰值频率点处对应的振型。叶片为三维扭曲结构，然而在试验中忽略了叶片复杂的构型，将其几何形状简化为平板。这种简化虽然会带来少许误差，但基本符合叶片的结构，而且振动方向主要是沿着叶身平面的法线方向，所以可以体现出叶片的振型图。

因为叶片类似于悬臂梁结构，理论上叶片根部为固支边界条件，叶根处节点振型幅值应该为0。实际测试中，叶片是通过夹具连接在振动台上，振动台和夹具不可避免会对叶片振型产生影响。根据叶片上述的动态特性，对提取的模态参数进行取舍，舍弃叶根处振幅较大的振型，认为这是叶片和夹具、振动台的耦合振型，不能作为叶片自身的模态。最终叶片工作变形分析得到模态参数见表1，振型如图4所示。

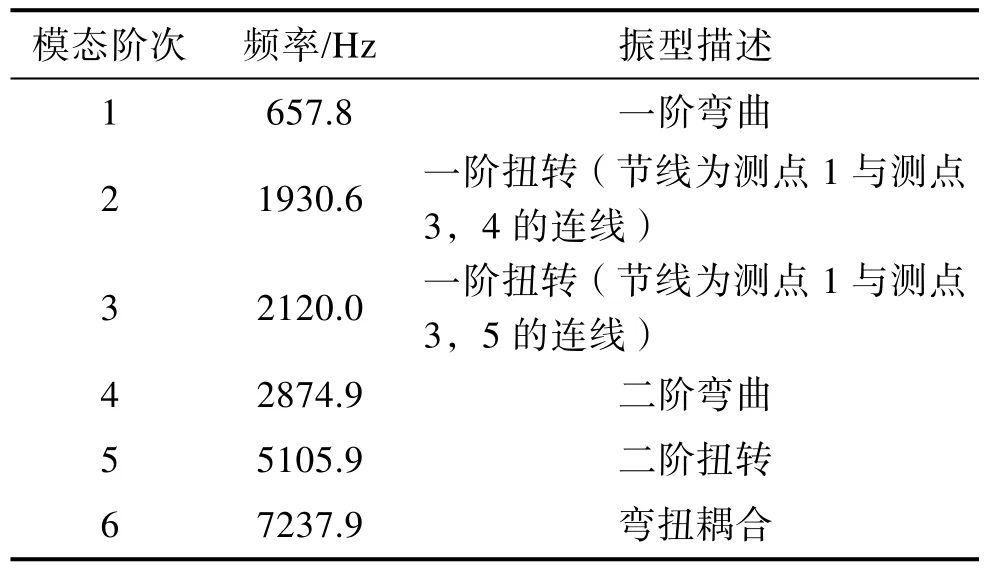
表1 叶片工作变形分析得到模态参数

由表1和图4可知，ODS方法识别出该叶片在10 kHz频率范围内的前6阶模态，其振型依次是一阶弯曲、一阶扭转（节线为测点1与测点3，4的连线）、一阶扭转（节线为测点1与测点3，5的连线）、二阶弯曲、二阶扭转、弯扭耦合。该叶片的振型测试结果主要由弯曲、扭转、弯扭耦合组成，这符合发动机叶片动态力学性能的特点。需要说明的是，该叶片的质量分布不均匀，所以存在两种不同一阶扭转模态，其区别在于节线位置不同。

为了评价上述振型的相关性，可以通过模态置信准则（Modal Assurance Criteria，MAC）来进行判定。FMAC函数是评价两个振型向量的相关性的量化标准，如果FMAC值等于1，则表明两个振型向量完全相同；如果 FMAC值等于 0，则表明两个振型向量完全不相关，是正交的；FMAC值越接近1，表明两个振型向量越相关。FMAC函数的表达式为：

式中：φr和φs分别表示两个振型向量。

假设结构为比例阻尼，对结构不同阶次的模态振型加权质量矩阵或刚度矩阵，结果具有正交性，具体表达式为：其中

如果结构的质量均匀分布，则结构不同阶次的模态振型也具有正交性，即不同阶次的模态振型的FMAC值为0。

基于模态置信准则理论，计算ODS方法测得的叶片前6阶振型之间的FMAC值，结果如图5所示。由图5可知，描述同一模态振型的两个向量，其FMAC值均为 1，不同模态振型的两个向量的 FMAC值都小于或等于0.2。其中第1阶与第2阶、第2阶与第3阶、第3阶与第4阶之间的FMAC值稍高，分别为0.15、0.18、0.2，其他阶次之间的FMAC值都小于0.1。由于实际的叶片阻尼不完全是比例阻尼，且该叶片的质量分布不均匀，所以不同阶次振型 FMAC值小于或等于0.2在可接受范围内，验证了ODS方法测得的模态结果的可靠性。

4 结论

文中采用结构工作变形分析理论，借助扫描式激光多普勒测振仪多点、非接触、高精度测量的优点，搭建了一套发动机叶片工作变形分析试验系统。通过振动台对叶片施加快速正弦扫频的基础激励，用测振仪测量叶片表面55个测点的速度响应，然后用工作变形分析方法得到了该叶片的前 6阶固有频率和振型。最后计算不同阶次振型之间的模态置信准则，证明了工作变形分析结果的可靠性。

基于本文的研究结果，得出如下主要结论。

1）基于扫描式激光多普勒测振仪搭建的ODS试验系统，可以测得叶片的固有频率和振型，通过验证振型之间的模态置信准则，证明结果的可靠性。

2）ODS方法通过在FODSFRF上选取峰值得到模态参数，避免了复杂的频响函数拟合过程，测试分析过程简便，实时性好。但ODS方法只能得到固有频率和振型，不能得到阻尼比，且选取峰值时具有一定的主观性。

3）采用ODS方法测得了叶片的模态参数，结果表明，该叶片在10 kHz频率范围内具有6阶模态，振型依次是一阶弯曲、一阶扭转（节线为测点1与测点34的连线）、一阶扭转（节线为测点1与测点35的连线）、二阶弯曲、二阶扭转、弯扭耦合。