多腔穿孔消声器传递损失理论计算与结构优化

2018-10-11罗汉明范昊天

制造业自动化 2018年9期

周毅，罗汉明，范昊天

（1.同济大学新能源汽车工程中心，上海 201804；2.同济大学汽车学院，上海 201804）

0 引言

发动机引入涡轮增压器可以增强动力性同时改善排放及消耗，但涡轮增压器本身也是一个重要的噪声源，会产生中高频率的宽带噪声。传统的共振性消声器只能衰减窄频带的噪声，无法抑制中高频率的宽频噪声[1]。单纯的阻性消声器由于其消声的幅值在整个频率范围内有限，因此也无法完全消除增压器的宽频噪声。而目前的主动噪声控制技术尚不成熟、装置复杂、技术难度大。另外，目前的发动机舱低矮化设计的趋势使得原本较为紧凑的发动机舱空间更为狭小，使得消声性能与安装空间之间的矛盾更为突出。

穿孔消声器类似于赫姆赫兹消声器，声波穿孔时产生的阻抗效应可明显地提高消声性能，中高频消声能力好且消声频段较宽，能同时兼顾消声性能和安装空间。通过对环形共振腔数目、直径和宽度的调整可以实现较好的宽频消声效果。

在穿孔消声器的理论计算方面，由于穿孔部分往往是多孔薄壁结构，要用解析法描述每个孔中的声波传播是非常困难的，通常用穿孔部分的声阻抗来表示该部分的声学特性，因此最关键的就是确定穿孔部分的分声阻抗。国内外学者针对穿孔消声器的传递损失进行了研究。文献[2]建立了声阻抗模型并通过试验发现流速对声阻抗率具有较大影响[2]。文献[3]通过试验的方法提出了考虑声抗阻率的公式[3]。在国内文献[4]拟合出了包括穿孔率、流速和频率对声阻和声抗影响的经验声阻抗率模型[4]。

上述的研究都是基于单腔结构且未涉及工程优化。实际由于涡轮增压发动机噪声频带宽，幅值大，单腔的穿孔消声器不能满足使用要求，因此将多个穿孔消声器连接起来，组成多腔穿孔消声器来满足涡轮增压发动机的降噪要求。

因此，本文首先基于声学一维传递矩阵法建立理论解析算法模型，并使用理论解析法计算出穿孔消声器的传递损失，并采用有限元的方法以及试验方法对理论计算。

结果进行试验验证。在方法得到验证的基础上，利用理论解析法研究穿孔消声器结构参数对消声性能的影响规律，并针对降噪目标曲线对该穿孔消声器进行结构参数优化，然后根据优化后的参数对消声器结构进行改进，从而确定最佳的实际方案。

1 多腔穿孔消声器传递损失理论计算

1.1 多腔穿孔消声器的理论解析算法

传递矩阵法是目前消声器消声特性研究中中常使用的计算分析方法，其引入使得消声器声学性能计算变得更加简单[5]。传递矩阵法的基本思想是把复杂的声学系统划分为若干个基本的声学单元，计算出每个声学单元的传递矩阵，将所有单元的传递矩阵相乘即可得到系统的传递矩阵，从而计算出消声器的传递损失。

单腔穿孔消声元件结构如图1所示。为简化理论推导过程，做出如下假设[6]：1）在穿孔管和环形空腔截面上声压和流体密度恒定；2）在穿孔管和环形空腔中的声压的幅值予以忽略；3）消声元件内能量损失仅仅由穿孔管和环形空腔之间的阻性引起的；4）消声元件中媒介的温度相同。

图1 单腔消声器结构示意图

在穿孔管部分，穿孔管内测的声压和质点振速分别为p1和u1，穿孔管外侧膨胀腔内侧的声压和质点振速分别为p2和u2，在简谐波假设下,管道内和腔内的声波方程分别为[4]：

式中，M1，M2分别为穿孔管内、膨胀腔内的马赫数，k0是波数，d是穿孔管直径，D是膨胀腔内径，ρ0为空气密度，c0为空气中声速，ρ0c0ζ为穿孔管声阻抗，ζ为穿孔管声阻抗率。

在不考虑流速的情况下，穿孔管声阻抗率模型如下：

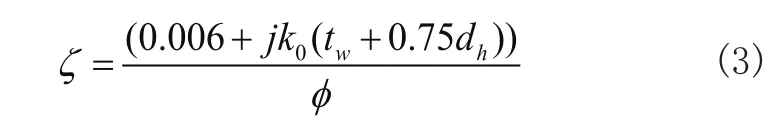
式中，tw为穿孔板厚度，也就是穿孔深度，dh是小孔直径，φ是穿孔率，j是虚数单位，利用穿孔板声阻抗建立穿孔管内和膨胀腔内的声压关系：

通过运算可得到穿孔管两端的传递矩阵：

进而求得单腔穿孔管的传递损失：

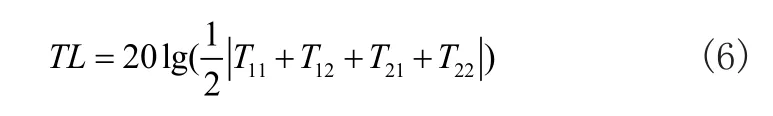
在线性声学范畴，沿管道轴向各消声单元的状态变量是线性相关的。因此，一个多腔消声器可以看成是多个单腔消声器串联起来而成，每个单腔消声器的状态变量为声压和质点速度，将沿轴向的各个穿孔腔的传递矩阵连乘起来，就可以得到整个多腔穿孔消声器的总传递矩阵[7]。

因此，对于多腔消声器，总的传递矩阵为：

多腔穿孔消声器的传递损失为：

运用上述一维解析算法，对本文研究的多腔穿孔消声器进行无流条件下的传递损失理论计算。本文所研究的多腔穿孔消声器的结构图、结构参数图以及运用解析法计算结果，分别如表1、图2、图3所示。

表1 多腔穿孔消声器结构参数

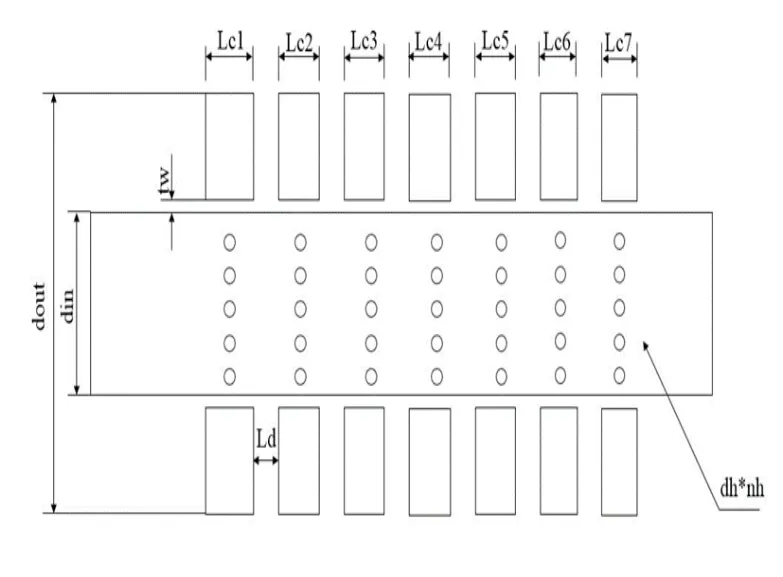
图2 多腔穿孔消声器结构示意图

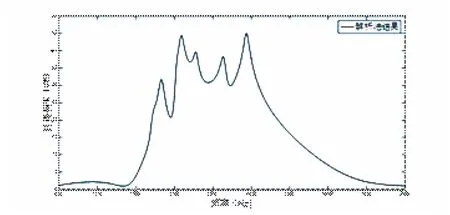
图3 一维解析法传递损失曲线

1.2 多腔穿孔消声器传递损失试验验证

将本文所研究的七腔穿孔消声器安装在双声源法传递损失测量台架上。双声源法是由Munjal和Doige在1990年第一次提出[8]，并被列入标准ASTM E2611-09[9]。双声源法利用四个传感器和传递矩阵法来测量消声器的传递损失。双声源法试验台架以及本文所研究七腔穿孔消声器安装方法分别如图4、图5所示。传声器安装间距为25mm，传递损失范围为490～5300Hz。

图4 双声源法试验台

为了分析一维理论计算与三维有限元和试验传递损失间的精度关系。本文采LMS Virtual.Lab软件中的Acoustic模块，将多腔穿孔消声器的三维网格模型导入软件中，运用声学有限元法AFEM对声学元件进行仿真，计算传递损失在频域上的分布情况。将多腔穿孔消声器的试验传递损失、一维理论计算和三维仿真所得传递损失同时显示在图6中。从传递损失图形形状和趋势上看，一维理论计算、三维声学仿真及试验传递损失结果存在较好的一致性。从传递损失频率范围方面分析，在频率1700～4000Hz范围内，一维解析方法的计算精度与试验的吻合度较好，三维仿真计算结果与一维解析法和试验结果相比消声频率范围要窄一些。因此可以使用该一维解析法来比较精确地预测多腔穿孔消声器的传递损失。

图5 七腔穿孔消声器传递损失试验

图6 多腔穿孔消声器一维理论计算、三维声学仿真及试验传递损失

2 多腔结构参数对消声特性的影响

2.1 分布式多腔穿孔消声器

多腔穿孔消声器由多个单腔穿孔消声器组合而成，常见多腔穿孔消声器的各个腔之间通过环形叶片间隔，环形叶片的厚度很小（一般小于2mm），因此可以看作多个单腔穿孔消声器直接连接而成。对于多腔穿孔消声器，本文提出了一种新的结构，间隔分布多腔穿孔消声器，结构示意如图7所示。

穿孔腔沿着主管道间隔性地分布开，假设一共有n个穿孔消声器，共有n-1个间隔等截面管道，因此整个消声系统可以看作n个穿孔消声器单元和n-1个等截面单元组成。穿孔消声器单元的传递矩阵在1.1节中推出。对于等截面直管，其两侧声压和质量振速的传递矩阵为：

图7 间隔分布多腔穿孔消声器结构示意图

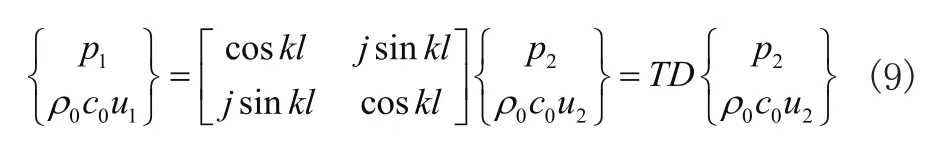
式中，l是等截面管的长度。基础消声系统总的传递矩阵可以写成：

其中TLi表示第i个单腔穿孔消声器的传递矩阵，TDi表示第i个等截面直管的传递矩阵，所有声学单元的传递矩阵连乘，即可求得系统的总传递矩阵。

2.2 分布式多腔穿孔消声器的消声特性

在本文所研究的多腔穿孔消声器中，穿孔管长度为30mm、穿孔率10%、孔径大小为3mm、穿孔管壁厚为3.1mm，外径与内径扩张比为61.4/33。传统连续多腔穿孔管消声器由三个同样的单腔穿孔管直接连接而成。保持穿孔腔参数不变，更改穿孔腔之间的距离，其长度分别为60mm、100mm、200mm的等截面管。利用解析法比较间隔分布式穿孔管消声器和传统连续多腔穿孔管消声器的传递损失，比较结果分别如图8所示。

图8 不同间距对传递损失的影响

分析上图中的结果可知，当间距为60mm时，传递损失最大值减小，但是低频段传递损失增加；分布式多腔消声器能在1000～3000Hz的频域内消除超过15dB的噪声，而连续多腔消声器只能在1500～3000Hz的频域内消除超过15dB的噪声，因此分布式消声频域更宽。随着间距的增大，传递损失最大值略有增加，峰值所在共振频率不变，有效消声频段变窄；对于穿孔腔间隔分布消声器的传递损失曲线，传递损失主峰值两侧波形呈现明显周期性特征，峰值由中心向两侧衰减，主峰两侧新出现的波形是由插入的间隔等截面管道引起，且波谷频率受间隔管道长度影响。

由上述不同的间隔距离的计算表明，间隔插入管引起的传递损失波谷所在频率直接影响到消声器总的传递损失和消声频段，因此对这一波谷所在频率的预测十分重要。因此通过调整穿孔腔之间的间隔距离，可以调整消声器传递损失的波谷频率，进而改进整个消声器的消声特性。

3 基于理论解析法的多腔穿孔消声器优化设计

3.1 遗传算法

遗传算法是一类模拟达尔文生物进化论的一种随机化搜索方法。遗传算法是从一个由随机形成的个体组成的初始种群开始，对每一代种群的个体进行适应度评估的一种优化方法[10]。本文借助MATLAB软件中自带的遗传算法优化工具箱，结合消声器一维解析算法来对该多腔穿孔消声器进行优化设计。

在本文中，优化目标频段在1500～3500Hz，期望的消声量为30dB。优化目标函数的数学方程如下：

其中tar_f(f)是目标曲线方程，ori_f(f,x)是原始曲线方程，x是要优化的变量，f1和f2表示目标频段的下限频率和上限频率，Object_(x)是要优化的目标函数，它表示目标曲线与原始曲线在目标频段内形成的面积和，目标函数值越小，则表示曲线与目标曲线越接近。优化目的是选取最优变量，来得到目标函数的最小值。