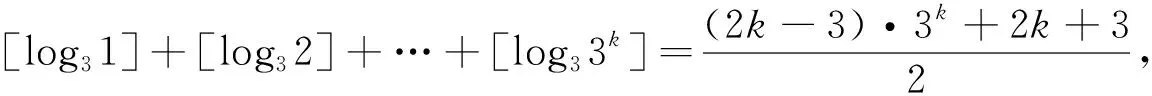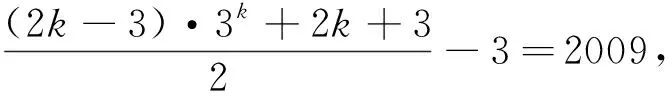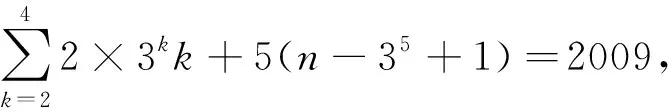由一道数学预赛试题引出的结论

宁夏彭阳县第四中学 (756599)

李艳玲

题目[x]表示不超过实数x的最大整数，则[log21]+[log22]+…+[log22012]= .(2012年河南省高中数学竞赛预赛试题)

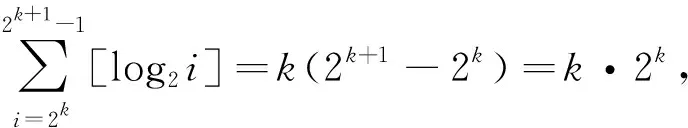
试题解答的关键是把[log21]+[log22]+…+[log2210]的求和转化为0·20+1·21+2·22+…+9·29的求和，这就涉及到等差乘以等比型数列求和的形式，通过指数比较，不难启发我们将问题进一步引申，得到下面的结论.

结论1 设f(x)=log2x(x∈N*),[f(x)]表示不超过实数f(x)的最大整数部分，记Sn=[f(1)]+[f(2)]+…+[f(2n)]，则Sn=(n-2)·2n+n+2.

证明:由2k≤x≤2k+1-1(k∈N)得，满足[f(x)]=k的x共有2k+1-1-2k+1=2k(个).于是有Sn=[f(1)]+[f(2)]+…+[f(2n)]=0·20+1·21+2·22+3·23+…+(n-1)·2n-1+n，设S=0·20+1·21+2·22+3·23+…+(n-1)·2n-1,①.给①两边同乘以2得2S=0·21+1·22+2·23+3·24+…+(n-1)·2n,②.由①减②(错位相减)得-S=2+22+23+…+2n-1-(n-1)·2n=2n-2-(n-1)·2n，所以，S=(n-2)·2n+2，故有[f(1)]+[f(2)]+…+[f(2n)]=(n-2)·2n+n+2(其中n∈N*).

对于底数为2的对数取整求和我们有上面的计算公式，那么，当对数的底数是3时，是否也有相应的计算公式呢？经过探究有下面的结论.

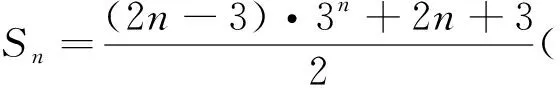
比较结论1和结论2的结果，我们发现它们有章可循，于是不难得出猜想，当对数的底数为4时，有下面的结论.

结论3 设f(x)=log4x(x∈N*),[f(x)]表示不超过实数f(x)的最大整数部分，记Sn=[f(1)]+[f(2)]+…+[f(4n)]=

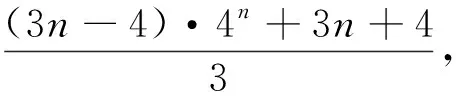
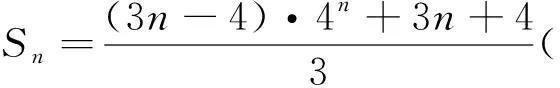
类似的，对于底数为5、6、…，可以写出相应的结论.限于篇幅，本文不再赘述.通过猜想归纳，我们便可以得到一个更一般的结论.

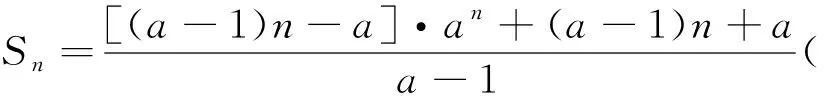
证明:(数学归纳法)(1)当n=1时，左边S1=[f(1)]+[f(2)]=1，右边=

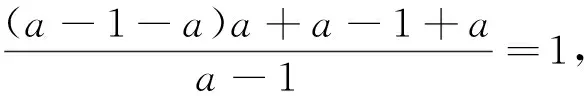
(2)假设当n=k时等式成立，即Sk=[f(1)]+[f(2)]+…+[f(ak)]

当n=k+1时，Sk+1=Sk+

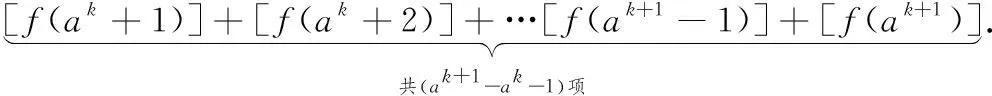
所以，当n=k+1时，等式成立，由(1)和(2)知，对一切的n∈N*等式成立.

下面看结论的应用

题[x]表示不超过实数x的最大整数，若[log36]+[log37]+…+[log3n]=2009，试确定整数n的值.(2009年北京市高一数学竞赛预赛试题)