平面向量问题的切入点探究

江苏省海门中学 (226100)

曹亚东

由于向量表示方法多、联系知识广、解题思路灵活，学生在学习平面向量时有这样的困惑:“老师，平面向量既有数的特征又有形的特征，请您告诉我们在求解平面向量问题时到底何时从数入手何时从形入手好呢？”本文通过对一道平面向量问题的多角度分析，谈谈我是如何让学生寻找到平面向量解题切入点的.

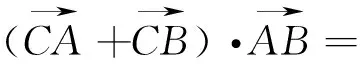
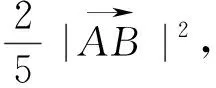
一、从代数角度探究

“如果没有运算，向量只是一个‘路标’，因为有了运算，向量的力量无限.”正因为有了向量的代数运算，才使得向量的问题变得多姿多彩.本题如果从代数运算的角度有以下三个切入点.

切入点一：从代数变换入手探究

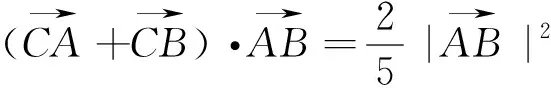
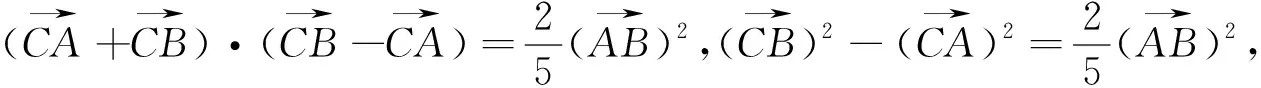
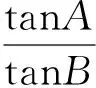
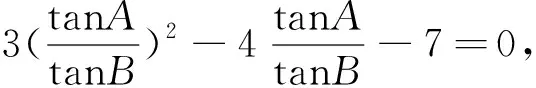
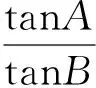
切入点二：从向量数量积的定义入手探究

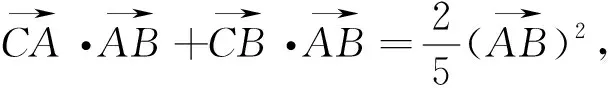
解法三比解法一、二来的简洁，关键在于直接将向量数量积用向量的模和夹角的余弦来表示.象这种以三角形为背景的向量问题一般采用边角互化来完成.所以，从已知结构入手，将题设中给出的信息和我们学过的公式、定理等等沟通起来，不然就不太容易找到解题突破口.

切入点三：用坐标法入手探究

用坐标来表示向量，本质就把向量问题转化成了代数问题来求解.

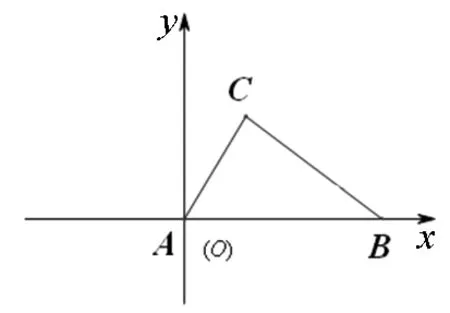
图1

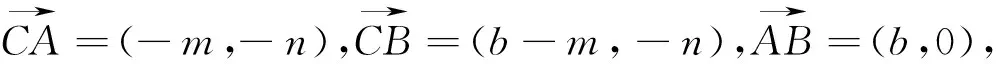
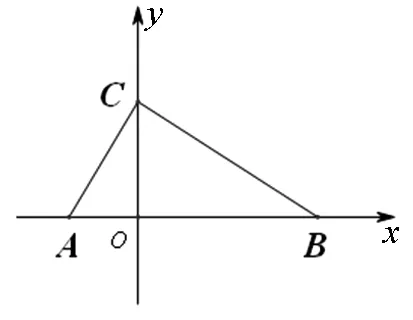
图2

当然也可如图2建系，方法同解法四.

解法四坐标法求解思维程度要求不高，是比较简单的一种解法.因此，在解决向量问题时，一般涉及到夹角为特殊角的问题优先考虑建系用坐标法求解，若不行，再考虑要用其它的方法处理.

二、从几何角度探究

向量的代数运算非常重要，但向量毕竟不是数量，它是既有大小又有方向的量，有向线段是其最直观和贴切的表示，若所有的向量题目纯粹用代数运算，而不能数形结合，则似单腿走路，必定行之不远，所以我们考虑从数形结合的角度来研究.

切入点四：从数形结合的角度入手探究

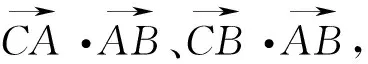
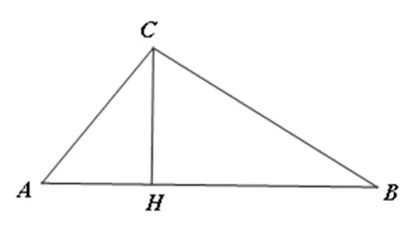
图3

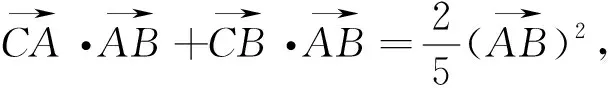
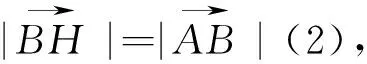
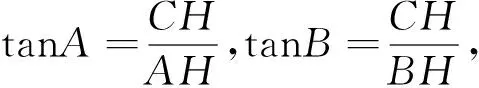
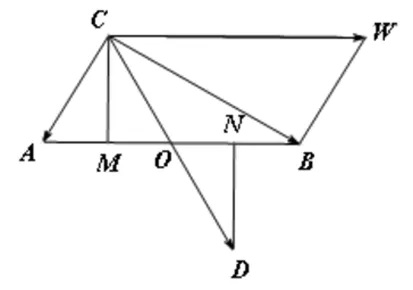
图4

解法六：如图4，取AB中点为O，连接CO并延长至点D，使得CO=OD，过点C、D分别作边AB的垂线，垂足分别为M、N.

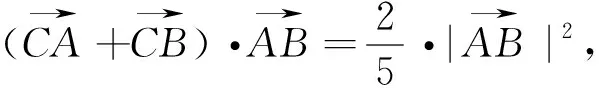
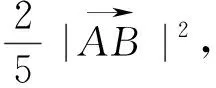
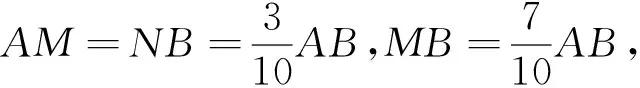
数形结合是解决平面向量问题的最重要的数学思想，所以必须让学生熟练掌握和理解向量各种运算的几何意义，引导学生多从数形结合角度去解决平面向量问题，多利用平面几何中的图形性质，不仅可以简化运算，还能大大提高解题的准确率.解法五的数形结合只是利用了数量积的几何意义，显得格外的简洁明了.同样的数形结合利用解法六就不是那么容易想到，技巧性比较高.从上面的几种解法我们看到利用数形结合解题非常快捷，但对学生的要求比较高，它需要我们的学生牢固掌握一些概念和运算的几何意义，以及曲线的代数特征，然后利用题目中的条件和结论等分析它的几何意义，从而达到数向形的转化.

以上介绍了几种向量问题解题切入点的探究方法，实际上向量问题的解题切入点远远不止以上几种方法，它需要我们在平时解题过程中多注意思想方法的积累并将它灵活运用.只有根据具体问题具体分析，凭借积累的经验、直觉和灵感等不断尝试探索，从而快速而准确地找寻到具体而恰当的解题方法，这才是学好数学之关键所在.