圆锥曲线中的最值问题

广东省深圳市南山区教育局数学教研室 (518052)

周爱国

圆锥曲线中的最值问题是高考中的热点问题，是从动态角度研究解析几何中的数学问题，体现了圆锥曲线与三角、函数、不等式、方程、平面向量等代数知识之间的横向联系，综合性较强，也是集中考查学生的转化能力、逻辑推理能力、综合分析问题与解决问题的能力，是考查转化与化归思想、函数与方程思想、数形结合思想等知识的好素材，所以往往备受高考命题者的青睐．由于圆锥曲线的最值问题与曲线有关，所以利用曲线性质求解是其特有的方法．除此之外，它与函数中的最值求解也有类似之处．下面介绍几种常见求解方法．

1．定义转化法

|PF|+|PA|的最小值为 .

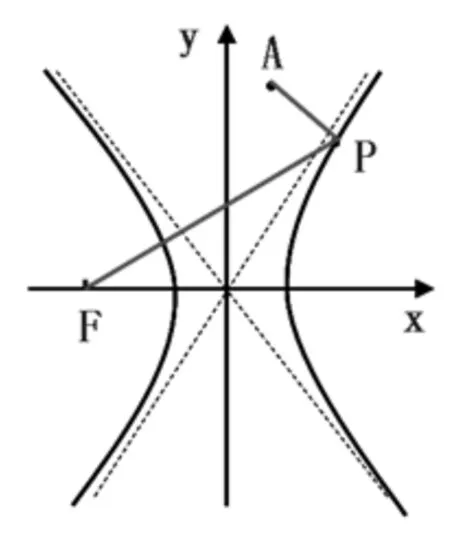
图1

解析:如图1,设双曲线的右焦点为F′，根据双曲线定义，有|PF|-|PF′|=2a=4，从而有|PF|+|PA|=

|PF|-|PF′|+|PA|+|PF′|=2a+|PA|+|PF′|，此时把问题转化为求|PA|+|PF′|的最小值，显然，当且仅当A,P,F′三点共线时取得，其最小值为|AF′|=

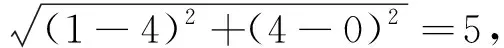
评注:根据圆锥曲线的定义，把所求的最值转化为平面上两点之间的距离、点线之间的距离等，这是求圆锥曲线最值问题的基本方法．本题借助双曲线的定义把|PA|+|PF′|的最小值转化为A,F′两点间的距离，从而求得|PF|+|PA|的最小值．

变式已知点M是抛物线y2=4x上的一点，F为抛物线的焦点，A在圆C：(x-4)2+(y-1)2=1上，则|MA|+|MF|的最小值为 ．

(参考答案：依题意得|MA|+|MF|≥

(|MC|-1)+|MF|=(|MC|+|MF|)-1，由抛物线的定义知|MF|等于点M到抛物线的准线x=-1的距离，结合图形不难得知|MC|+|MF|的最小值等于圆心C(4，1)到抛物线的准线x=-1的距离，即为5，因此所求的最小值为4．)

2．切线法

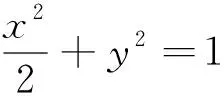
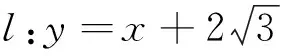
变式在抛物线y=4x2上求一点，使该点到直线y=4x-5的距离最短．

3．参数法

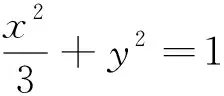
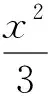
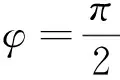
评注:根据曲线方程的特点，用适当的参数表示曲线上点的坐标，把所求的最值归结为求解关于这个参数的函数的最值的方法．本题充分利用了椭圆的参数方程，把两个最值问题转化为三角函数的最值问题，简洁优美．

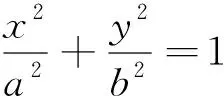
4．函数法

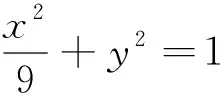
解析:先让Q点在椭圆上固定，显然当PQ通过圆心O1时|PQ|最大，因此要求|PQ|的最大值，只要求|O1Q|的最大值．设Q(x,y)，则|O1Q|2=x2+(y-2)2①

因为Q在椭圆上，则x2=9(1-y2)②

评注:把所求最值的目标表示为关于某个变量的函数，通过研究这个函数求最值，是求各类最值最为普遍的方法．本题将所求最值转化为二次函数的最值，使问题的解答过程酣畅流利．

变式在抛物线y=4x2上求一点，使该点到直线y=4x-5的距离最短．

5．几何法

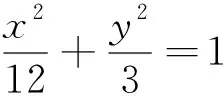
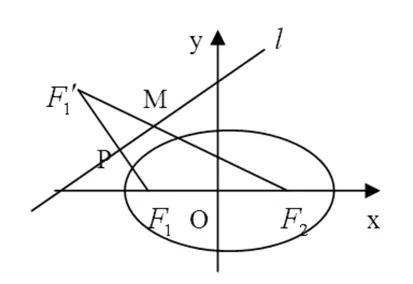
图2

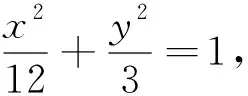
评注:将圆锥曲线的最值问题转化为平面几何问题中的最值问题，再利用平面几何知识，如对称点、三角形三边关系、平行线间距离等求解，本题的解答恰好利用了对称的思想，同时也充分体现数形结合的思想．

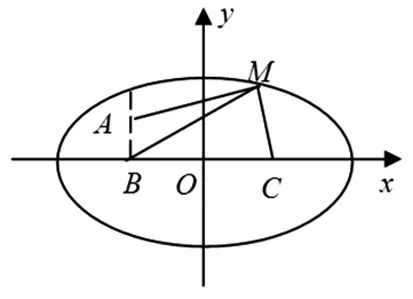
图3

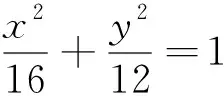
(参考答案：根据椭圆定义，有|MB|+|MC|=2a=8，∴|MA|+|MC|=|MA|+(8-|MB|)=8-(|MB|-|MA|)，为使|MA|+|MC|取得最小值，只需|MB|-|MA|取得最大值，此时必有A、B、M三点共线时才可以取得，这时有|MB|-

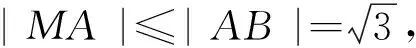
6．基本不等式法

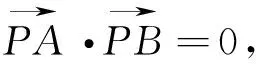
(2)求直线AB的方程(用x0,y0表示)；

(3)求△MON面积的最小值．(O为原点)．

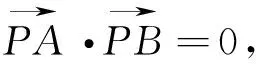
(2)设A(x1,y1),B(x2,y2)，则PA、PB的方程分别为x1x+y1y=4,x2x+y2y=4，而PA、PB交于P(x0,y0)，即x1x0+y1y0=4，x2x0+y2y0=4，

∴AB的直线方程为：x0x+y0y=4．

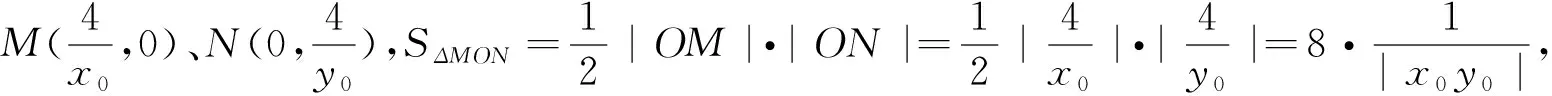
评注:先将所求最值的量用变量表示出来，再利用基本不等式求这个表达式的最值．这种方法是求圆锥曲线中最值问题应用最为广泛的一种方法．本题在最后一问求解面积的最值时用到了基本不等式．

变式已知定点F(0，1)和直线l1：y=-1，过定点F与直线l1相切的动圆圆心为点C．

(1)求动点C的轨迹方程；

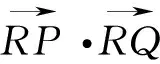
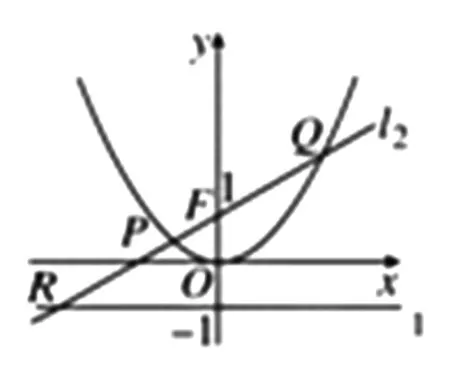
图4

解析：(1)由题设点C到点F的距离等于它到l1的距离，∴点C的轨迹是以F为焦点，l1为准线的抛物线．∴所求轨迹的方程为x2=4y．

(2)由题意直线l2的方程为y=kx+1，与抛物线方程联立消去y，得x2-4kx-4=0．如图4，记P(x1，

y1)，Q(x2，y2)，则x1+x2=4k，x1x2=-4．

∵直线PQ的斜率k≠0，易得点R的坐标为