解析几何中有关动点最值题的解法探析

江苏省启东市汇龙中学 (226200)

殷春华

动点问题是解析几何中常见的问题，而且常常与解析几何中的最值问题有紧密的联系.遇到此类问题，学生经常束手无策.在“动”的过程中，寻找“定”，是解析几何的核心问题之一.这类问题，常可以对动点运动规律的探寻，利用点的轨迹来解决.现举几个例子加以分析说明.

类型一：动点的运动轨迹是直线，利用点与直线的距离求最值.

例1 过动点P作圆C：(x-3)2+(y-4)2=1的切线PQ，其中Q为切点，若|PQ|=|PO|(O为坐标原点)，则|PQ|的最小值为 .

思路：本题中，点P是动点，PQ与PO均在变化.但圆C是个确定的圆，故PQ可利用切线长定理求出，PO可利用两点间距离公式求出.这两个量在求解过程中，均要用到点P.因此，设出点P的坐标为(x,y)，就可以得到关于x,y的等式，即为动点P的轨迹方程.由于|PQ|=|PO|，所以求|PQ|的最小值就是求|PO|的最小值.而动点P的轨迹已经求出，从而可以比较容易地解决问题.

解析：设点P(x,y)，因为PQ与圆C相切，所以PQ2=PC2-r2=(x-3)2+(y-4)2-1.又PO2=x2+y2.由PQ=PO知PQ2=PO2，得到(x-3)2+(y-4)2-1=x2+y2，化简可得3x+4y-12=0，即点P的轨迹是直线l:3x+4y-12=0.因为PQ=PO,所以求PQ的最小值即求PO的最小值.而PO的最小值就是求一定点O到直线l:3x+4y-12=0上一动点的距离的最小值,显然点O到直线l的距离最短.因此PQmin=POmin=

类型二：动点的运动轨迹是圆，利用点与圆的位置关系求最值.

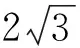
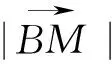
解析:以AB边所在的直线为x轴，AB的中垂线为y轴建立直角坐标系.

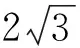
类型三：动点的运动轨迹是直线，利用直线与圆的位置关系求最值.

例3 已知圆x2+y2=4上有且只有四个点到直线12x-5y+c=0的距离为1，则实数c的取值范围为 .

思路:在平面内，到直线12x-5y+c=0的距离为1的动点的轨迹是与该直线平行且距离为1的两条直线l1和l2.现在圆x2+y2=4上要有四个点到直线12x-5y+c=0的距离为1，因此，直线l1与l2均必须与圆x2+y2=4都有两个公共点，即直线l1与l2均必须与圆x2+y2=4都相交.利用直线与圆的位置关系就可以求出实数c的取值范围.

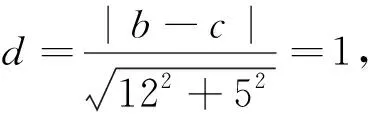
类型四：动点的运动轨迹是圆，利用圆与圆的位置关系求最值.

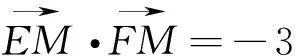
图1

由|PQ|=|PA|可求得动点P的轨迹为一条直线，又由圆与圆的位置关系可把问题解决.如果此题能从探索动点的轨迹这个角度去思考，就能把比较难的问题转化为简单的问题.

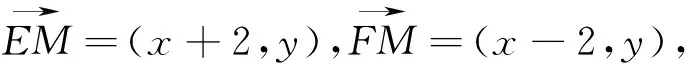
上述动点与最值结合的问题，初看时均不知从何入手.经过仔细分析后，发现动点均有一个共同特征：即动点最终均满足某个等式.从而可以探索出动点所在的某个曲线，再解决最值问题就显得比较容易.

类型五动点的轨迹确定，利用对所求量变化趋势的探索求最值.

图2

例5 设点M(x0,1)，若在圆O：x2+y2=1上存在点N，使得∠OMN=45°，则实数x0的最大值为 .

思路:本题点M与点N，事实上均为动点，且点M的轨迹已经确定是直线y=1，点N的轨迹是圆O.如果两点同时运动，本题将很难解决.

因此，我们可以先假定点M“不动”，为直线y=1上某一定点.

观察发现：当点N在圆O上运动时，∠OMN也在不断地变化(如图2).当点O,M,N三点共线时，∠OMN=0°，然后∠OMN慢慢变大；

当MN与圆O相切时，∠OMN最大.

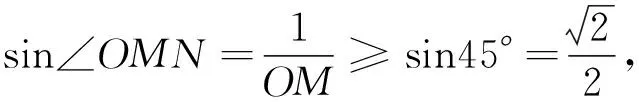
上述几种类型的解析几何问题，都存在着某些共同特征，重点是找到动点的运动规律.无论问题中的条件如何变化，很多问题最终都可能转化为点与线，点与圆，线与圆，圆与圆的位置关系来解决.当然，在教学中，我们仍然需要不断的归纳和总结，才能更好地面对可能遇到的新的问题.