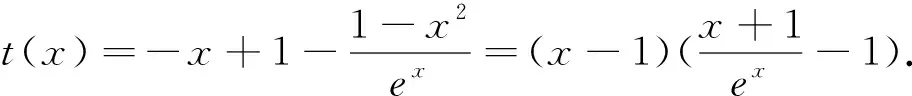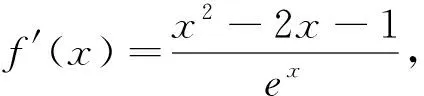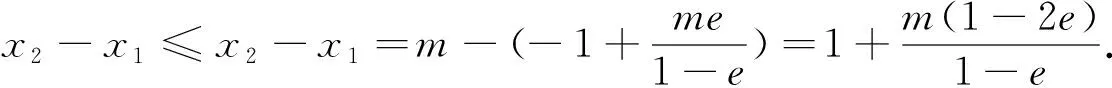函数零点巧变换 切线为媒显神威
2018-10-11广东省惠州市第一中学516007
中学数学研究(江西) 2018年9期
广东省惠州市第一中学 (516007)
方志平
有关函数零点的不等式证明问题,是近几年高考的一个热点问题.由于此类题目结构千变万变,设问方式各不相同,使得问题变得十分灵活.对于这类问题,我们如何进行思辨呢?又如何去解答呢?本文阐述的是一类借用切线证明有关函数零点的不等式问题,方法新颖,独具一格,赋有创意.这仅是此类问题的冰山一角,权当起抛砖引玉之用.

图1


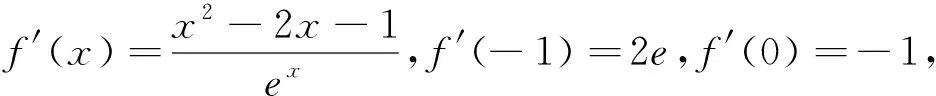
(1)先证明当-1 令h(x)=2ex+1-x2+2x+1,h′(x)=2ex+1-2x+2,令φ(x)=2ex+1-2x+2,∵x+1>0,∴φ′(x)=2ex+1-2>0,知φ(x)在(-1,1)上单调递增,∴φ(x)>φ(-1)=6>0,即h′(x)>0,h(x)在(-1,1)上单调递增,∴h(x)>h(-1)=0,即g′(x)>0,所以g(x)在(-1,1)上单调递增,∴g(x)>g(-1)=0,∴g(x)=2e(x+1)-f(x)>0,即当-1 图2 评注:本题若直接求解函数f′(x)=m的零点,简直是无法求得,由于本题证明的问题是关于函数零点差的不等式,并非是等式,于是数形结合,联想到借助曲线y=f′(x)与x轴交点处的两条切线为“媒”,将“函数零点差”巧妙放大为“两切线与直线y=m交点的横坐标的差”,从而使问题迎刃而解. 上述这种变换零点,依切线为“媒”的求解策略,使问题变得简洁、清晰,其解法使人耳目一新,彰显出其别具一格的魅力!同时也将数形结合的思想提升到了一个新的高度,这对提高学生解题能力和培养其学习数学的兴趣都大有裨益,另外,也为此类问题的推陈出新发挥着抛砖引玉的作用.