微专题让试卷讲评春风拂面

江西师大附中 (330046)

黄润华

考试是促进学生学习，检测教学效果的有效手段.试卷讲评反映教师的教学态度和教学智慧，是考试评价的核心环节，是发现并有效解决学生疑难的有效途径.一次区域统一考试命题倾注了命题团队大量的心血，着重考查学生的学科核心素养，所以必须科学评价考试，深入挖掘试题内涵，更加全面真实地了解学情，帮助学生查漏补缺，体会思想方法的运用，提升思维品质.教师依据试卷中的经典题、易错题或障碍题，搜集资料，深入探究，拓展延伸，类比分析，设计有针对性的微专题课，可以让试题讲评春风拂面.

2018届南昌市二模理科选择题第12题，是一道根基平实、思维要求高的题.

笔者以此题为核心，精心设计了一堂微专题探究课，引导学生学会分析问题，学会类比探究，学会回归本质，学会猜想验证，感悟触类旁通、融会贯通的学习境界.

1.对问题解决思路的分析

先根据题意画出草图，在图中标注已知条件，然后进行分析.

分析1：要求三角形AF1B内切圆的标准方程，关键是确定圆心的位置.

又圆心为某两条直线的交点，已知圆心在∠AF1B的角平分线上，所以关键是要探究圆心还会在哪条直线上.

分析2：若从动态控制角度看，F1A,F1B可关于∠AF1B的角平分线对称变化，交点A,B均在双曲线上，而双曲线的焦距已经确定，所以双曲线只有一个参数未定，故本题中双曲线是待定的.因此，反设双曲线去猜想内切圆的方程不合逻辑.

分析3：除∠AF1B的角平分线外，其他条件不确定，尝试猜想：三角形AF1B内切圆是否有什么特殊性质？其他两个角的角平分线显然不能得到，那么还有什么要素可以控制圆心位置呢？与内切圆圆心联系紧密的有：过切点且与该点处的切线垂直的直线，弦的垂直平分线和内角角平分线，结合图形去找出路.

2.对问题情境展开的联想

通过联想，充分运用已有的知识和方法解决新的问题，亦称化归思想，是人们解决问题的常用方法.本题中核心要素是双曲线和内切圆，双曲线的定义是隐藏条件，一般都要用到，还有三角形的内切圆满足的性质.结合平时的学习，容易联想到以下两个模型：

图1

模型1 双曲线焦点三角形的内切圆与实轴的切点是双曲线的顶点.

证明：如图1，|PF1|-

|PF2|=(|PC|+|CF1|)-(|PB|+|BF2|)=

|CF1|-|BF2|=|F1A|-

|AF2|=2a,又因为

|F1A|+|AF2|=2c，所以|F1A|=a+c，所以切点A为双曲线的右顶点.

模型2 和椭圆焦点弦相切的焦点三角形的旁切圆与长轴的切点是椭圆的顶点.

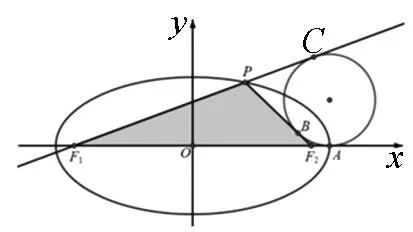
图2

证明：如图2，设圆切长轴于点A，切F1P的延长线于点C，则|F1C|+|F1A|=

|F1P|+|PC|+|F1F2|+

|F2A|=2c+|F1P|+

|PB|+|BF2|=2c+2a，又因为|F1C|=|F1A|，所以|F1A|=a+c，所以点A为椭圆的右顶点.

概括：第一个模型学生非常熟悉，第二个模型可能不熟悉，类比两个模型发现，其内切圆或旁切圆均与实轴或虚轴所在直线切于曲线的顶点.

3.对问题的联想产生的猜想

双曲线(或椭圆)的焦点三角形的内切圆(或旁切圆)都有特定的切点——顶点，本题中不再是焦点三角形，但仍可以理解为两个焦点三角形组合成的三角形，其依然紧密联系圆锥曲线的定义及内切圆的有关性质，这样我们就有理由结合草图作出猜想:ΔAF1B的内切圆与直线AB切于右焦点F2.

要证明猜想成立，只需证明|AF2|=|AP|.根据联想到的模型已经运用的方法可以完成证明.

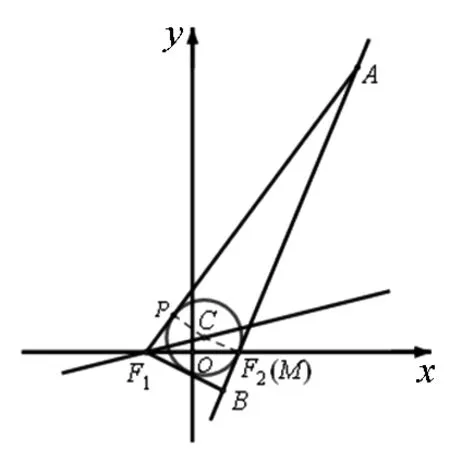
图3

证明：如图3，由双曲线定义知，|AF1|-|AF2|=2a,|BF1|-|BF2|=2a.设三角形AF1B内切圆切AB于点M，则|AP|+|AM|=

|AF1|+|AF2|+|BF2|-

|BF1|=2a+2|AF2|-2a=2|AF2|，又因为|AP|=

猜想是发现新问题，解决新问题的有效途径，在教学中需培养学生良好的思维习惯，形成大胆猜想、小心求证的思维品质.本题实质上是以内切圆为背景考查切线长定理及圆锥曲线定义的灵活应用，有新颖性.

4.对问题的探究进一步拓展

教师在进行试卷讲评课的设计时，为了进一步巩固圆锥曲线定义及三角形内切圆相关性质的理解，可以搜集有关资料进行创造继续引领学生展开探究.比如，笔者设计了如下两道题供学生思考.

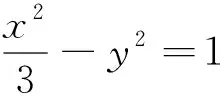
一石激起千层浪，对上述两个问题的充分思考与交流必将激起学生浓厚的学习兴趣，培养合作学习、探究拓展的思维习惯，引领学生从特殊到一般，先猜想定值的可能值，再想办法完成一般情形的证明.

经过一番热烈的研究与交流，同学们会惊喜地发现两个问题中的定值均为相应曲线的离心率，回顾小结问题解决的方法，容易得出一般结论.

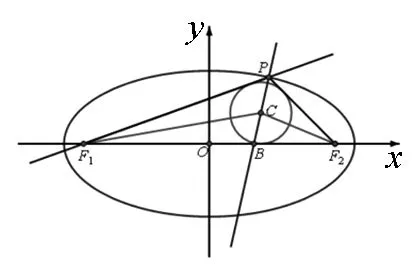
图4

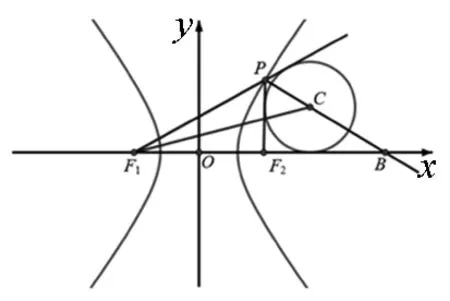
图5

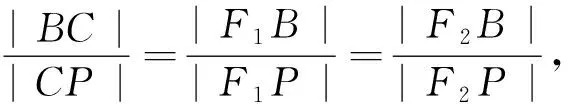
模型化思想是连通知识与应用的重要桥梁，模型化可以让问题系统形象，对于核心的知识与思想方法，教师应创造条件使问题分门别类，让学生触景生情，触类旁通.

本节微专题课经过一系列关联问题的探究，引导学生深化对圆锥曲线定义、内心的本质特征、圆的切线有关的性质、猜想验证和类比思想的理解与应用，有利于打通学生思维壁垒，感悟触类旁通、融会贯通的学习境界.