带槽齿结构弹丸侵彻半无限靶仿真研究
2018-10-11刘铁磊沈培辉梁化鹏
刘铁磊,沈培辉,梁化鹏
(南京理工大学 机械工程学院, 南京 210094)
在进行侵彻的相关计算时,为了建模的方便,对杆式穿甲弹的外形部分往往进行简化处理,即将弹丸槽齿部分简化为等直径的圆柱体结构。如黄俊清[1]采用等直径简化的方法,模拟了穿甲弹弹体侵彻靶板的过程;吴群彪[2]采用等直径简化的方法,研究了组合杆侵彻靶板的机理;焦志刚[3]采用等直径的方法,计算了钨合金杆体侵彻靶板的过程;赵晓宁[4]用等直径的方法,模拟了斜侵彻金属靶板的过程;章程浩[5]同样采用等直径的方法,对易碎弹侵彻靶板的过程进行了仿真研究。应该说,在过去主要研究单一杆的侵彻深度和长径比的关系时,采取上述简化方法是完全合适的。但是对于复杂外形杆,尤其是带有连接杆的分段杆,等直径简化方法不再合适。OrphalR等[6]率先对分段杆侵彻机理进行了研究,DAVID[7]则对分段杆侵彻斜靶板做了研究;在国内有学者通过数学的方法证明[8],分段杆的侵彻深度大于等质量的连续杆。邓云飞[9]做了有关分段杆侵彻的数值仿真,他认为在大多数情况下,带钨合金连接杆的非理想分段杆(TARSG)的侵彻效率最好。由于其文中TARSG的形状与弹丸槽齿部分的形状类似,因此对于杆弹槽齿部分不进行简化。为此,本研究围绕验证齿槽简化方法,对槽齿结构杆弹不同等效方法进行相应的分析计算,对杆弹槽齿部分的侵彻机理进行初步的研究。
1 理论分析
从表面看,杆弹的槽齿模型和全弹径模型存在差异。槽齿部分的强度较全弹径部分削弱,其次在其他外形尺寸相同的情况下,槽齿模型的质量较全弹径模型质量偏小,因此在进行分析时,要同时考虑上述影响。
根据弹丸在侵彻过程中的运动情况,可列出方程组:
(1)
这是破碎侵蚀过程中的方程组。其中:v是杆体运动速度;l为杆长;u为杆体侵蚀速度;p为侵彻深度;s为杆体截面积;ρ为杆体密度;k1、k2、k3为与靶板相关的材料系数。本式中取k1、k2、k3分别为[10]0.148、0.287、1。上述方程可以看出,带齿杆侵彻过程是不均匀的。
当ρtu2≤Yp时,破碎侵蚀停止[11]。若Yp>Rt,则杆体对靶体发生刚体侵蚀,有:
(2)
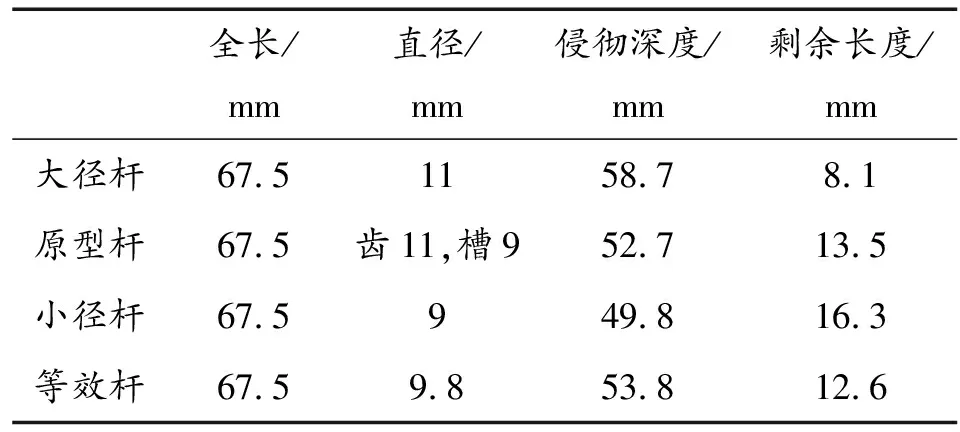
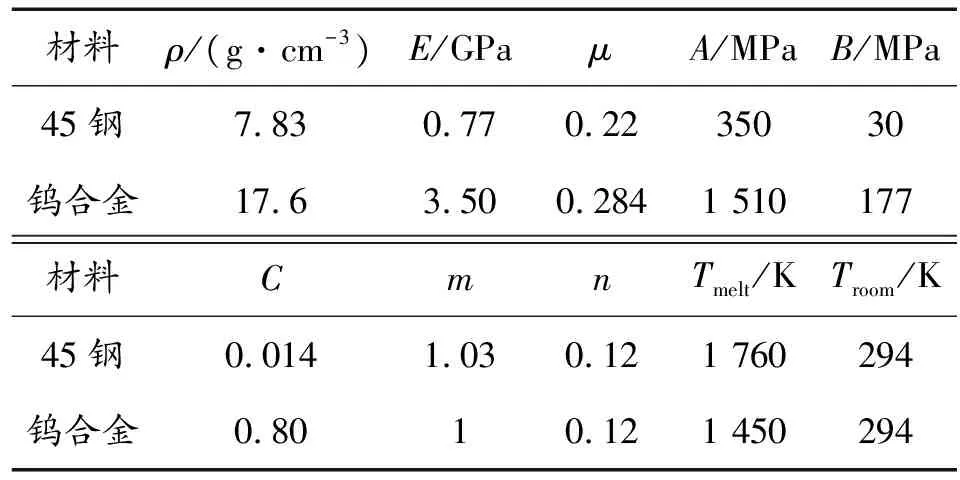
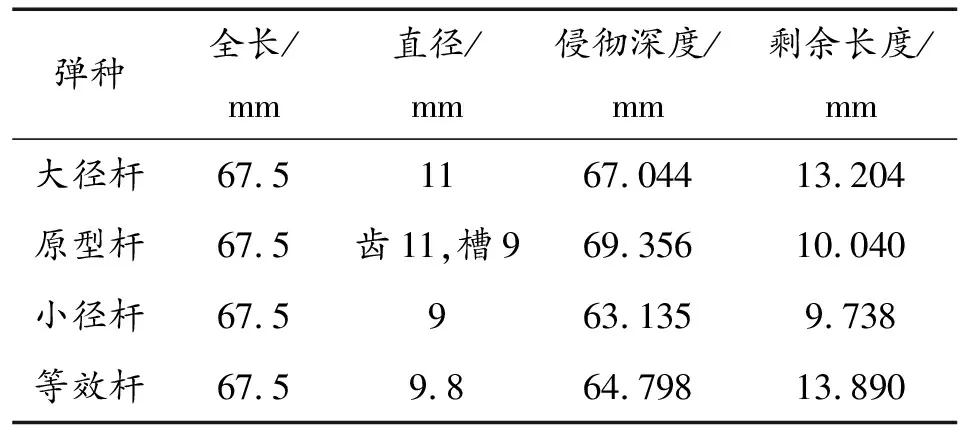
当Yp (3) 利用方程组式(1)、式(2) 、式(3),构成完整的齿槽杆体和简化杆体物理模型。在此基础上编制计算程序进行运算。其算法流程如图1所示。 为了给齿槽杆体提供一个计算准则。本文建立了4种长度相等的侵彻杆体模型,其中一种为齿槽杆,3种为简化杆。其形状如图2所示。为方便描述,这里把以齿径为计算准则的杆体简称为大径杆;把同时考虑齿槽直径的杆体简称为原型杆;以槽径为计算准则的杆体成为小径杆;而等质量等效杆体是与齿槽杆相同材料,等长,等质量的杆体,简称等效杆。主要用于消除图2(a)、图2(b)两杆不同质量的影响,同时验证以等质量杆体替代齿槽杆体,简化模型是否可行。 运用物理模型对杆的侵彻进行近似计算,计算结果如表1所示。 表1 工程计算结果 计算结果显示,在初始速度,初始长度相同的前提下,弹径越大,侵彻深度越深,残余杆剩余长度越短。原型杆的侵彻深度和剩余长度和等效杆接近。表明等效杆可较好地替代原型杆进行侵彻深度的计算。 为了更加直观地反映槽齿结构对侵彻的影响,在相同的速度,靶厚条件下进行了有限元仿真。其形状特征和仿真结果如图3,图4所示。仿真所用的材料参数源自实验室数据,其值如表2所示。 表2 材料参数 图3 4种不同杆体侵彻初始时刻示意图 图3、图4反映了侵彻开始时刻和侵彻终止时刻,侵彻体相对于靶体的位置变化情况。图3中,各杆体形状尺寸如图2,图3各靶板完全相同。从图4可以看出终止时刻,剩余杆体的长度并不相同。对于各杆的侵彻深度和剩余杆体长度在表3中列出。 通过计算节点坐标之差,可以测得两点间的位移。 表3 4种杆弹部分侵彻参数 仿真结果显示,初速相同,初始长度一致的前提条件下,弹径越大侵彻深度越大。这与工程计算结果基本一致。 由于四杆体的质量不完全相同,在相同的初速下。各杆体初始动能的大小关系如下: E大径杆>E原型杆=E等效杆>E小径杆 对比大径杆,等效杆,小径杆的侵彻深度,可知在简单圆柱体结构下,杆体的动能对侵彻深度的影响最大。若初始动能相同,则杆体结构成为影响侵彻深度的主要因素。表3的仿真结果显示,在一定条件下通过结构上的变化可使初始动能略低的弹丸取得更大的穿深。 比较图4中各杆体侵彻靶板产生的弹坑形状,可以发现槽齿结构原型杆的弹坑平均直径和小径杆相近,小于其余两个杆体侵彻产生的弹坑直径。这反映槽齿结构杆和小径杆在稳定侵彻阶段产生的扩孔耗能较其他两杆少,其动能更多地用于增加侵彻深度。 以槽齿原型杆和等效杆为例,对两杆的侵彻过程进行分析。从图5可以看出,槽齿杆和等效杆在侵彻过程中,均形成稳定的“蘑菇头”,但是“蘑菇头”的直径则与杆体直径相关。图5(a)中可以看出在侵彻过程中,齿槽部位破碎较为严重,因此稳定的“蘑菇头”大小取决于杆体的小径,而非大径,因此其尺寸小于等效杆侵彻形成的“蘑菇头”。 在侵彻过程中始终存在靶板金属轴向流动和径向流动。因此“蘑菇头”实际上对侵彻产生不利影响。当“蘑菇头”半径越大时,所受的阻力越大,使金属纵向流动的力也越大。弹体动能更多地消耗于开坑,而非侵深上。因此,原型杆在侵深上的能量利用率比等效杆更高。图4中可以明显看出原型杆形成的空腔直径明显小于大径杆和等效杆形成的空腔直径。其侵彻机理与邓云飞论文所述的TARSG侵彻机理类似,但由于原型杆的齿的强度远小于TARSG中质量块的强度,不能侵彻,故仿真中没有出现侵彻空腔呈现“葫芦串”的形状。 通过Matlab软件和LS-DYNA软件对槽齿原型杆和其简化杆进行仿真计算,仿真结果证明一般情况下,可以用光滑杆等效齿槽原型杆进行仿真计算,等效杆以等质量为原则,求出其等效直径;当杆体槽齿尺寸占比显著时,应充分考虑其外形,不宜等效处理。通过对齿槽原型杆侵彻机理的分析发现,对于相同尺寸大小的杆体侵彻目标时,齿槽原型杆侵彻深度略大于光滑杆,这对穿甲弹外形设计有参考意义。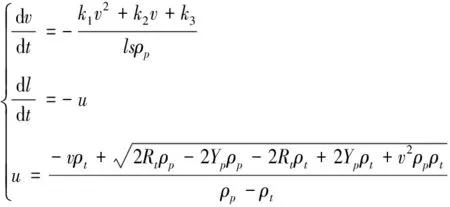
2 数值分析
3 结论
