跳台滑雪空气动力学研究进展

胡 齐，张文毅，陈 骐



跳台滑雪空气动力学研究进展

胡 齐1，张文毅2，陈 骐1

1.国家体育总局体育科学研究所, 北京 100061; 2.北京体育大学教务处, 北京 100084

跳台滑雪过程主要涉及弹道学和空气动力学因素，这主要决定了该项目的研究要求。从起跳台起跳瞬间跳台滑雪运动员身体重心的速度和位置决定了跳台滑雪飞行轨迹和飞行距离。空气动力学因素涵盖了运动员/滑雪板系统空气动力特性的各个方面。跳台滑雪过程通常分为4个不同的阶段：助滑、起跳、飞行和着陆。讨论总结跳台滑雪不同阶段所涉及的空气动力学研究成果，大多采用风洞试验测量或计算机模拟与实地现场研究相结合等方法。空气动力学在这些阶段中均起着重要的作用，且飞行阶段的研究最多。跳台滑雪飞行方式经历了由传统直立方式到V型方式的转变过程；助滑姿态是减小空气阻力以及提高助滑速度的关键；起跳及其随后的过渡到飞行阶段被认为是最重要的阶段，因为它们决定了运动员在飞行中初始条件和最终姿态；运动员/滑雪板系统飞行姿态对飞行阶段空气动力特性至关重要，同时运动装备（滑雪板和跳台滑雪服）、体重以及风环境等在飞行阶段也起着很大的作用；采用V型方式飞行着陆时会出现地面升力效应。建议在开展跳台滑雪空气动力学研究时重视滑雪板姿态以其结构参数、户外现场环境等因素。计算流体力学（CFD）和智能化风洞实验训练馆是跳台滑雪空气动力学研究领域未来可能的发展方向。

跳台滑雪；空气动力学；助滑；起跳；飞行；着陆；V型

1 前言

跳台滑雪是一项非常刺激、令人兴奋的雪上运动项目，运动员脚穿着特制的滑雪板，沿着跳台的倾斜助滑道下滑，借助速度和弹跳力跃入空中，并在空中飞行一段时间后在着陆坡上着陆。因此，跳台滑雪过程主要涉及弹道学和空气动力学两大方面。弹道学方面取决于运动员从起跳台上的飞行速度和起跳位置，空气动力学方面包括运动员/滑雪板系统的气动特性（速度、运动员/滑雪板系统的姿态、阻力和升力、服装设计、滑雪板长度等）。弹道学和空气动力学都对跳台滑雪运动员提出了特殊的要求，如应最大限度地提高垂直升力和减小阻力。跳台滑雪过程通常分为4个不同的阶段：助滑、起跳、飞行和着陆。空气动力学在这些阶段中均起着重要的作用，且飞行阶段的研究最多。本研究将总结跳台滑雪不同阶段所涉及的空气动力学研究成果，以期对跳台滑雪过程的技术要求有一个清晰的认识，并提出跳台滑雪空气动力学研究未来可能的发展方向。

2 技术发展水平

2.1 历史背景

从1924年第1届冬季奥林匹克运动会（冬奥会）起，跳台滑雪就一直是冬奥雪上项目。在20世纪20年代中期，最优秀的跳台滑雪运动员Thams（挪威）创造了一种新的飞行方式，即上半身弯曲保持较大的向前倾斜角度同时手臂伸展在前面并与滑雪板彼此平行，此项技术取代了此前直立的飞行方式，并在1936年以此方式跳跃距离首次达到 100 m。早在1926年，Straumann[43]开创性地第1次在风洞中开展跳台滑雪空气动力学研究，同时利用运动方程建立了第1个跳台滑雪力学的解析模型。到20世纪50年代中期时，瑞士跳台滑雪运动员Däscher第1个采用上半身弯曲保持尽可能大的向前倾斜角度并且保持手臂向后靠近身体的飞行方式，此飞行方式来自Straumann在1954年为了获取更好的空气动力而进一步开展风洞研究的结果[42]，此研究为Däscher提供了一个最佳的气动飞行姿态。

为更深入了解跳台滑雪的空气动力学原理，Tani等[44]进行了大量的飞行力学风洞试验研究，测量了作用在全尺寸运动员模型上的气动力和俯仰力矩，提出了最好的飞行姿势，即手臂应该靠近身体的一侧，并指出，最大升力阻力比（L/D）的姿态并不会带来最远的飞行距离。同时，Grozin[13]提供了更多的风洞试验研究数据及结果，包括以迎角（α）为参数的气动力升力系数（CL）和阻力系数（CD）之间的关系，此数据几乎涵盖了运动员和滑雪板姿势的全部范围，这些都是在实际跳台滑雪过程中会出现的。Remizov[34]利用Grozin的数据解决了最优飞行问题，即运动员必须如何改变迎角才能获得最大的飞行距离。理论分析结果表明，迎角逐渐增大时，最大飞行距离是由一个凸函数实现的，该凸函数的形式取决于各个气动参数。Jung等[16]最近发现了类似的结果，当初始速度为30 m/s时，与最佳飞行轨迹相比，在整个飞行过程中保持最大CL/CD比值常数的飞行姿态，跳跃距离损失13 m，保持最大CL值时跳跃距离损失10 m。Denoth等[7]进行了实验现场研究，认为此前Remizov在飞行阶段的理论优化是有问题的，特别是在飞行早期阶段，他们指出，优化必须包括跳台滑雪的所有阶段。此外，来自波兰的研究小组Maryniak等[21]利用基于风洞模型试验的数学方法为跳台滑雪运动员姿态对空气动力学影响的研究作出了很大贡献。

2.2 V型飞行方式取代经典飞行方式

虽然是波兰运动员Graf首次展示采用了在跳台滑雪中“革命性”的飞行方式——V型飞行方式[22]，但由于瑞典运动员Boklöv采用此V型飞行方式取得了巨大成功，才因此吸引了更多人对这种飞行方式的优势进行较为详细的研究。最重要的关于V型方式的研究由Mahnke等[18]首先开展，他们进行了一系列的风洞实验，同时分析V型方式与传统方式相比的优势。紧接着，Cutter[6]开展了关于V型飞行方式的空气动力学研究，使用一个缩比模型系统(1∶5.5)在美国空军学院航空实验室的亚音速风洞中进行风洞试验，试验结果认为，V角为22.5°、迎角为20°（这被认为是运动员将滑雪板转向相对于运动方向更平坦的最大可行方法），其最佳的L/D比为1.55。此后，由于教练员迫切需要了解更多关于V型飞行方式的优势，在V型飞行方式应用的早期进行了多项研究[14,15,28,38,45,59]。与以往的平行飞行方式相比，多数研究表明，V型飞行方式具有更好的气动性能，而且V型方式使运动员能够更多地向前倾斜。Jin等[14]提出，V型飞行方式对初始角速度相当敏感，并且认为跳台滑雪运动员不能在初始角速度超过17°/s的情况下旋转。很快，人们就发现，如果把雪靴绑在滑雪板上更靠后一点的话，他们可以更向前倾斜。但这种方法由于俯仰力矩不平衡而会产生非常高的翻滚风险。之后，基于一些分析研究[28]，从1994-1995赛季开始，国际滑雪联合会将雪靴之前的滑雪板长度占总滑雪板长度的最大百分比限制在57%。此外，也已开展了其他一些关于V型飞行方式优势的研究[40,41]。

3 跳台滑雪不同阶段的空气动力学研究现状

跳台滑雪过程涉及到4个阶段，助滑、起跳、飞行和着陆，每个阶段都对飞行距离有重要影响。起跳阶段及其随后的过渡（约0.5 s）可能是整个跳台滑雪过程中最关键的阶段，因为它们决定了初始飞行速度、起跳角度、角动量和飞行过程中运动员姿态。空气动力学在这些阶段中均起着重要的作用，运动员/滑雪板系统所受的气动力可以用下列方程来描述：

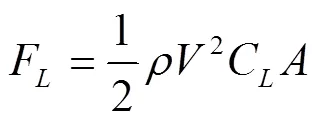
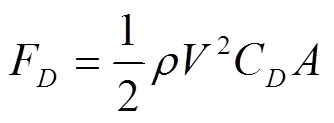
其中，F为气动升力，F为气动阻力，为空气密度、为速度、为投影面积、C和C分别为升力系数和阻力系数。

3.1 助滑阶段

尽管助滑速度是影响飞行距离的最重要因素，但目前尚未针对助滑阶段开展广泛的研究[37]。在助滑过程中，运动员助滑前行的空气阻力应尽可能低，从而实现加速度最大化。空气阻力主要取决于运动员的姿势和阻力面积，它通常被表示为CA，其中，阻力系数C代表流线型程度。Virmavirta[48]开展了助滑阶段运动员气动力的风洞试验研究，图1显示了3位运动员助滑姿态对应空气动力的测量结果，通过这些力值给出了CA的估算值，即运动员A和B的CA估算值分别为0.084和0.150。由此可以看出，运动员的身高越高并不一定意味着其空气阻力越大。当阻力面积为0.20 m2时，上述CA值给出的阻力系数分别为0.42和0.75，表明两种运动员助滑姿势的气动特性有很大的差异，其中，气动升力（F）的差异更大。在助滑过程中，气动升力应该尽可能接近于零，而在速度滑雪中，气动升力是重要影响因素，因为它可以减少滑雪摩擦[31]。Thompson等[46]通过风洞试验研究获得了速度滑雪者的阻力系数为0.160。由于运动员在跳台上的助滑姿势必须为起跳提供最优的初始条件，因此，空气动力学并不是这一阶段需要考虑的唯一因素。Ettema等[8]的研究讨论了气动阻力作用下的这些初始条件。

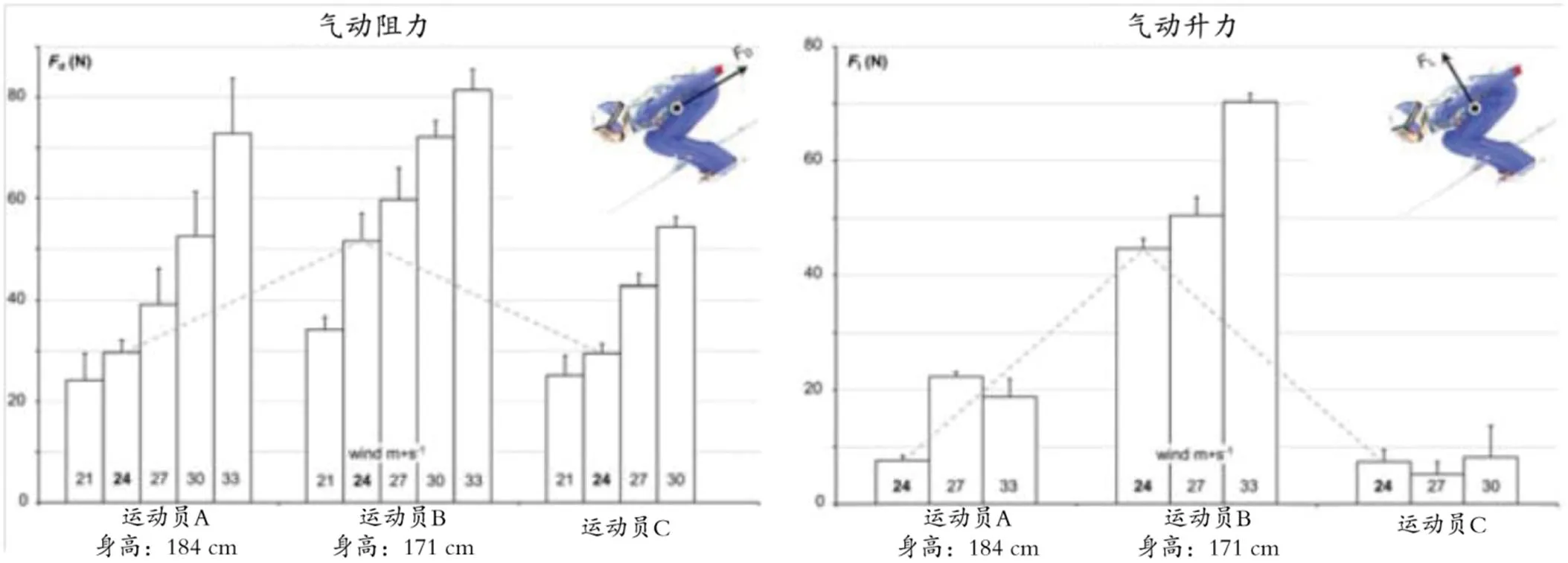
图1 风洞中测得的3位运动员助滑姿态对应空气动力示意图

Figure 1. Aerodynamic Forces during the In-run Position of Three Jumpers Measured in Wind Tunnel

注：此图修改自Virmavirta[48]的研究。

3.2 起跳阶段

在跳台滑雪起跳过程中，其弹道特性体现较为明显，尽管早些时候已经针对其气动特性提出了一些预测[56]，但起跳时空气动力学的作用还没有得到广泛的研究[25,54,55]。从空气动力学角度来看，起跳是非常关键的，因为运动员总是在最大限度地提高垂直加速度和最小化空气阻力之间妥协，他们在起跳时很快就暴露在空气中从而产生阻力。基于一系列风洞实验，Virmavirta等[55]得出结论，在起跳过程中气动升力有助于运动员，即减轻运动员在真正起跳动作中所受的负荷，负荷的减少会导致起跳时间的缩短和更高的力量发展速度。同时，Virmavirta等[55]的力结果是通过测量地面反作用力获得的，包括起跳力和气动力，因此，起跳时瞬态的气动升力仍未能被直接测量出来。但通过使用平均加速度方程以及平均力方程，在无风和有风条件下平均力的差异可以计算出起跳时平均升力值。Müller[25]也做了类似的风洞测量试验，并在这些测量中，通过在滑雪板下使用滚轮来模拟助滑跑道与滑雪板之间的低摩擦状态。此外，Keizo等[17]采用计算流体力学（Computational Fluid Dynamics ，CFD）技术研究了运动员在起跳过程中姿态对气动特性的影响，着重比较两种不同姿态的起跳情况，研究认为，起跳过程中气动特性在较短的时间内发生了动态变化，两种起跳方式的气动特性差异较大。

图2 滑雪运动员在实际跳台中与在风洞中起跳动作的对照图[47]

Figure 2. Comparison of Ski Jumper’s Take-offs between Wind Tunnel and Actual Jumping Hill Conditions[47]

但是，如何最有效地利用起跳阶段的气动升力仍然是个未知数，特别是在这个阶段任何有意的技术动作都很难完成。在实际跳台条件下，起跳训练时间仅限于短短几秒钟，但需花费很长的准备时间。因此，为了增加训练量，运动员通常会采用模仿起跳方式，包括滚轮滑雪板/平板[9]。而提高运动员对气动力主观感觉的最佳方法是在风洞中进行起跳，图2将跳台滑雪运动员在实际跳台中与在风洞中起跳动作进行比对[47]，这两种情况的技术动作有很大的相似之处，也就是说，可以利用风洞进行起跳训练，但是，在常规训练中使用风洞的费用相对较高。

3.3 飞行阶段

在起跳后，运动员应该在飞行阶段早期尽快达到一个稳定的飞行位置，并确保受到小阻力[31]，同时应完成向后和向前旋转角动量的完全平衡[37]。跳台滑雪运动员在0.5 s内完成飞行姿态的稳定[49]，并且在这个短时间内（约为 15 m的飞行距离），运动员几乎不能进行任何有意的姿态调整，也可以说起跳阶段决定随后的飞行姿态。同样，这也意味着起跳时所发生的错误不能在飞行阶段得到有效纠正，而成功起跳的优势可能会因飞行过程中的错误而丧失。一般来说，飞行阶段可以被认为是整个跳台滑雪过程中气动特性体现最为明显的部分。诸多对跳台滑雪飞行阶段气动特性的研究[1-3,12,16,19,20,28-30,33,35,36,41]采用了风洞试验测量或计算机模拟与实地现场研究相结合等方法。Gardan等[12]采用CFD方法探讨迎风角和速度对气动力的影响，数值结果表明，在早期飞行阶段速度对升力系数和阻力系数的影响很小，相反，迎风角变化对作用于运动员身体上的升力和阻力有很大的影响。实地现场研究结果的典型例子如图3所示，这些结果表明，世界一流滑雪运动员在飞行初期后的位置角变化不大[28,35]。Chardonnens等[4]引进了一种基于惯性传感器的新三维技术来评估稳定飞行的总气动力。该系统所提供的所有动力学参数，除质量中心的平均力略低之外，均在以往基于静态测量系统的研究范围内。根据2002年冬季奥运会大跳台比赛结果，Virmavirta等[49]的研究很好地阐述了从早期到稳定飞行阶段的临界转变，并给出了早期飞行阶段运动员速度分量的平均值，同时通过详细比较两名优秀跳远运动员早期飞行阶段的各动力学参数，可以看出在飞行阶段保持速度的重要性。

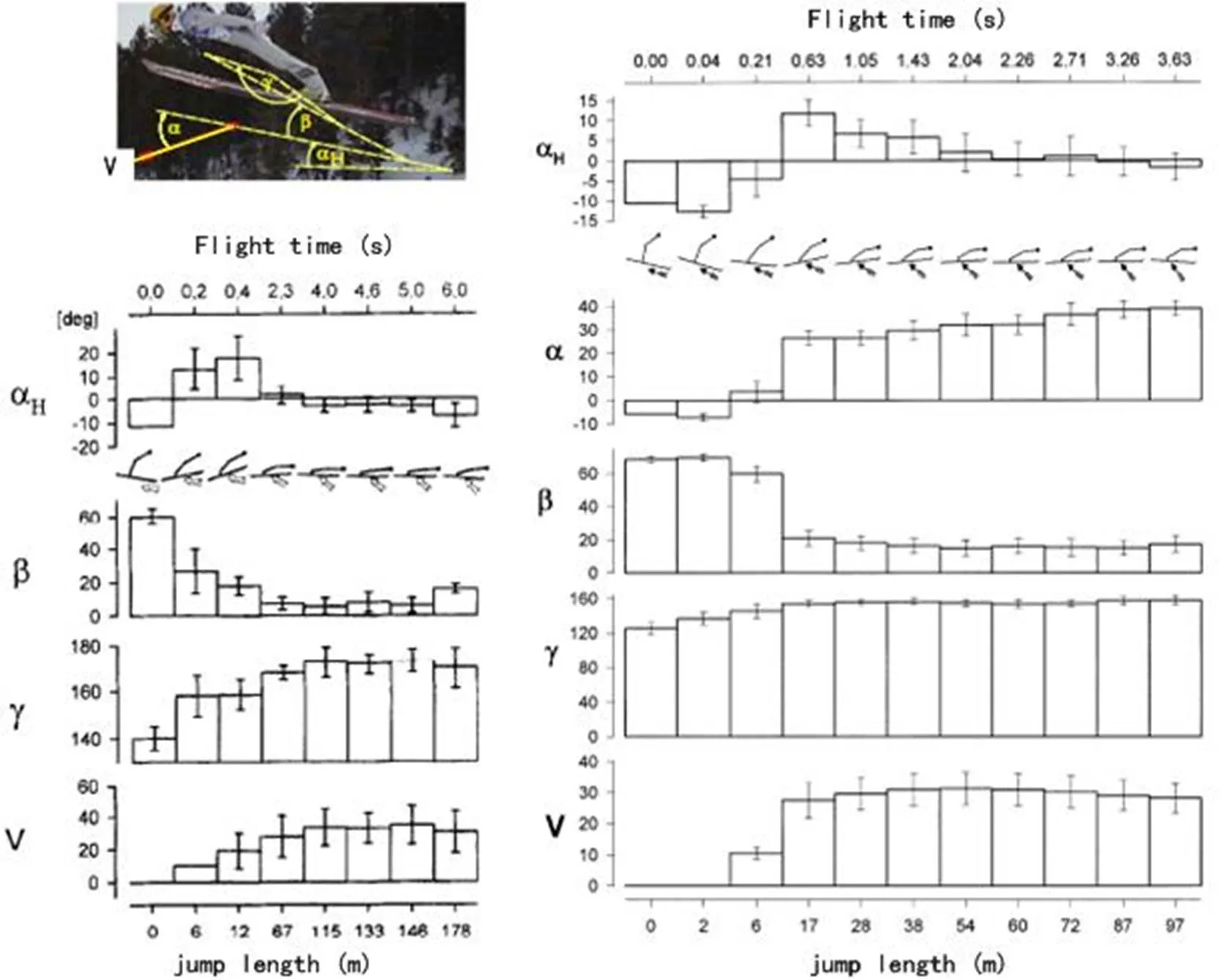
图3 两种不同现场测量手段下世界级跳台滑雪运动员的姿态角度变化

Figure 3. Position Angles of the World Class Ski Jumpers in Two Different Field Measurements

注：此图修改自Müller等[28]， Schmolzer等[35]的研究。

普遍认为，滑雪器材（滑雪板和跳台滑雪服）在跳台滑雪飞行阶段起着很大的作用。近年来，为了使气流经过滑雪板时更加平缓，在飞行过程中滑雪板姿态越来越受到人们的关注。Virmavirta等[50]通过风洞试验研究单个滑雪板空气动力特性，将滑雪板悬挂在六分量风洞平衡测量装置上（图4）。从测量结果可以看出，升力随着V角（滑雪板夹角）的增大而增大，而边缘角的有害影响似乎也随着V角的增大而增大。同时，具有零边角的大V角仍然改善了气动升力系数，但是，具有如此张开宽度的V角的飞行姿态可能变得不稳定。当然，纯粹从空气动力学的角度来看，单个滑雪板显然在侧面飞行效果更好。此实验研究方法或多或少偏理想化，显然并不是所有的结果都适用于真实飞行阶段。在V型飞行方式中，在运动员伸展腿部时，滑雪板自然地绕着纵轴线转动边缘，为了保持滑雪板更加平坦，运动员在滑雪板的后部使用弯曲的棍子，作为滑雪靴的后部和绑带之间的连接件。Seo等[41]通过风洞试验还研究了运动员/滑雪板整体系统的俯仰力矩情况。

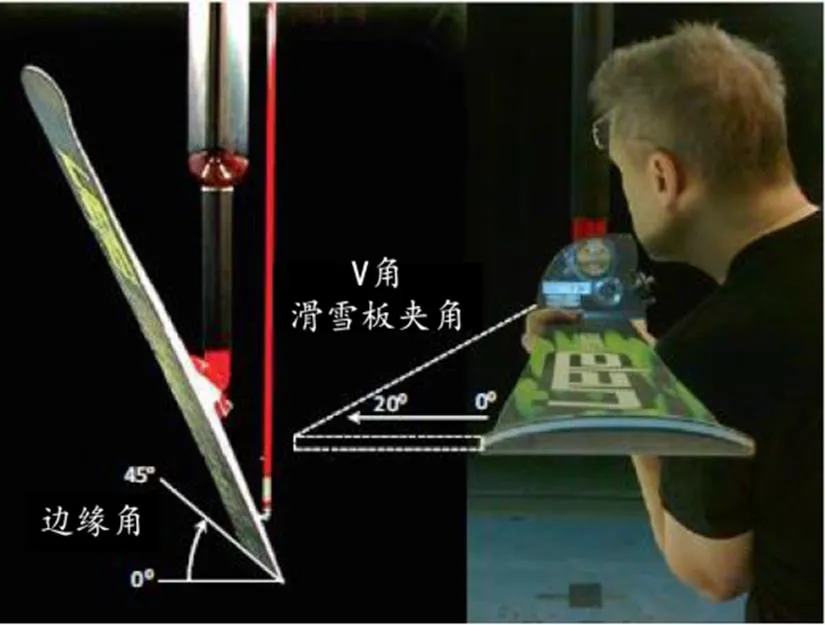
图4 测量单个滑雪板的风洞平衡装置示意图

Figure 4. Wind Tunnel Set-up for the Measurement of the Isolated Ski Jumping Ski

注：此图修改自Virmavirta等[50]的研究。

由于运动员不断寻求气动特性更好的装备，跳台滑雪服的设计也发生了多次修改。跳台滑雪服主要影响飞行阶段的气动力，但也可能影响起跳速度，因此，过去的所有修改都增加了空气动力学效应，增加了飞行距离。目前，已发表的有关跳台滑雪服研究的文献很少[5,23,51]。当跳台滑雪服的大小和厚度的显著性效果被充分研究掌握时[51]，由于会产生太大的飞行距离，国际滑雪联合会（FIS）通过跳台滑雪服改变规则试图限制其空气动力特性。由于在连续风洞试验中运动员的姿态再现性较低，因此要采用全尺寸模型进行跳台滑雪服研究（图5）。运动员只能粗略估计空气流动中跳台滑雪服的适合性和气动情况。但通常修改后的跳台滑雪服之间的变化相对来说很小，导致预期的差异将被由于风洞中模型的连续修整之间的差异掩盖。Meile等[23]重点比较研究了3种不同的跳台滑雪服：1）紧身跳台滑雪服；2）符合现行规定的跳台滑雪服；3）适中尺寸的跳台滑雪服。研究发现，跳台滑雪服对空气动力特性影响较大，因为所研究的细小差异可能对飞行距离有决定性的影响。在FIS试图控制跳台滑雪服的空气动力学特性期间，在规定范围内，有时甚至超出规定的范围，运动员总是试图修改他们的跳台滑雪服以改善其空气动力学特性。最近一次有关修改跳台滑雪服的规则[10]就是要求额外的不可伸展的皮带应该被缝制在套衫的腰部内，以防止运动员把跳台滑雪服的裤裆向下移，这样能够改善跳台滑雪服的空气动力学。

众所周知，重量的大小在体育项目中是非常重要的，重力因素往往会限制运动表现。在21世纪初，跳台滑雪运动员为寻求低体重的优势导致产生一些严重的体重不足的问题[24,26,27,36]。因此，FIS在2004年制定了一项规则，决定通过将滑雪板最大长度与身体质量指数（BMI）联系起来解决这一问题，使得低体重将不再有吸引力，并为不同体重的运动员提供更公平的成功机会。目前，运动员的BMI不低于21时，滑雪板最大长度为运动员身高的145%；运动员的BMI低于21时，采用BMI每降低0.125则滑雪板长度降低0.5%的控制手段[10]。然而，在这项规则生效后，很明显，滑雪板长度的减少并不能完全抵消低体重的优点。Virmavirta等[52]研究探讨了滑雪板长度和体重减少对飞行距离的综合影响（图6），BMI在21以下飞行距离的优势仍然是BMI每减小0.5飞行距离增加1 m左右，此调节手段仅仅抵消了35%~38%的低体重优势。这是因为滑雪板只覆盖了运动员/滑雪板系统的部分空气动力区域。当然，跳台滑雪中低体重问题也可以作为其他体育项目解决策略的一个启发式例子[26]。使用较短的滑雪板，特别是在早期飞行阶段，可能不允许运动员像使用滑雪板较长的运动员那样具有较强的前倾能力，但滑雪板长度减少的极限是未知的，高度依赖于运动员的个人技术特征与水平。

图5 跳台滑雪运动员与全尺寸模型的风洞试验测量示意图[24]

Figure 5. Wind Tunnel Measurements of a Ski Jumper and a Full-sized Model[24]

此外，风环境对跳台滑雪的空气动力学有巨大影响。Müller等[28]的研究数值计算表明，从有利方向吹出3 m/s的恒定风速，可使185 m的飞行距离增加16 m；而从不利方向吹来的风速使飞行距离减少23.7 m。Seo等[40]也探讨了风对飞行距离的影响，认为在风速为1 m/s的情况下，飞行距离约为130 m的相对得失为4 m。为使比赛更公平，使赛事能够在不断变化的风条件下顺利进行，FIS在风洞数据和计算机模拟的基础上，于2010年推出了涉及风与助滑跑道的补偿系统[11]，即Δ=TWS(HS-36)/20，其中，Δ为风对飞行距离（m）的影响，TWS为平均切向风速（m/s），HS为跳台尺寸（m）。值得注意的是，就风速而言，对飞行距离的影响是线性的。Virmavirta等[53]对风环境与上述补偿系统在跳台滑雪过程中的作用进行了验证，结果表明，风速为3m/s时，迎风与逆风对飞行距离的影响不呈线性关系（迎风时增加17.4 m、逆风时减少29.1 m），由于随着着陆坡度的降低，飞行距离的变化速度也随之减慢，所以，上述补偿系统采用的线性公式仅适用于有限的飞行距离范围。

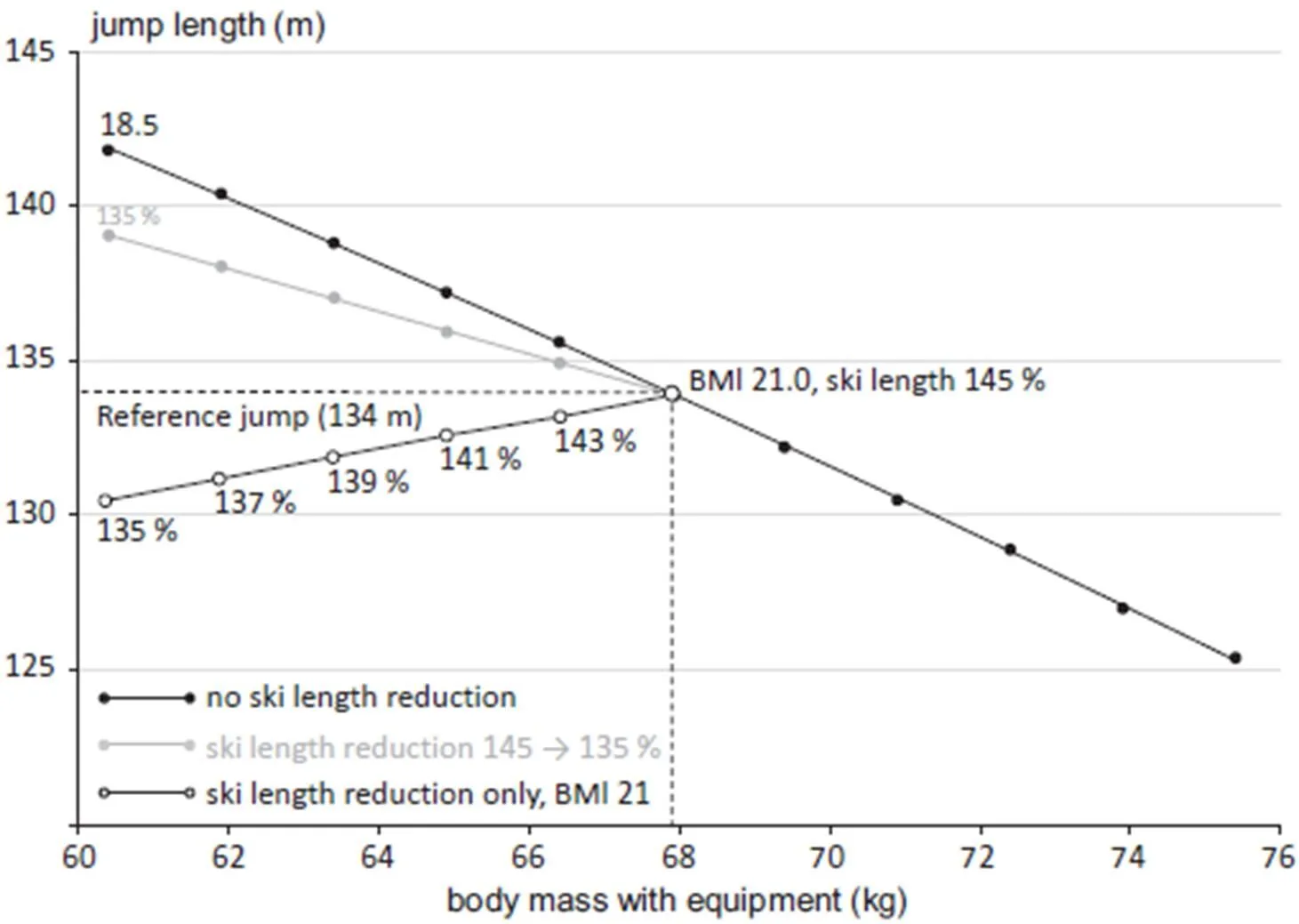
图6 滑雪板长度和体重减少对飞行距离的综合影响[52]

Figure 6. Combined Effect of Body Mass and Ski Length Reduction[52]

3.4 着陆阶段

“屈膝旋转技术”即双腿膝盖弯曲同时一条腿在另一条腿前面，是跳台滑雪着陆阶段的重要技术组成部分，不使用此技术的运动员可能会损失多个分数点，相当于几米的飞行距离。从空气动力学的角度来看，当运动员在着陆接近地面时，经历了一个边界条件，这可能会改变通过身体的气流。这种地面效应对跑道上的飞机和水面上的水鸟的性能很重要，因此，Ward-Smith等[57]的研究认为，此效应在跳台滑雪着陆阶段也很重要。为了模拟地面对运动员的影响，他们在地面间隙高度可调的风洞中使用了滚动地和缩放比例模型。Ward-Smith等[57,58]的研究指出，跳台滑雪运动员并没有承受任何由于地面上升产生的升力。但Seo等[39,40]表示，Ward-Smith等研究使用的雷诺数小于实际雷诺数，而他们自己的V型飞行方式地面效应的空气动力学数据在实际雷诺数的范围内。在采用全尺寸模型的地面效应测量装置中，在风洞的整个试验段上方设置了一个地面板，而且滑雪板尾部与此地面板的间隙很小，同时为了模拟地面附近的飞行，应使用滚动地。Seo等[41]发现，带地面板的升力面积总是大于无地板的升力面积。随着滑雪板夹角角度的增加，带地面板和不带地面板的升力面积差异增大，在传统的滑雪板平行飞行方式中没有类似的地面效应。

4 未来发展方向

计算流体力学（CFD）已经被认为是未来提高对跳台滑雪过程认知的重要工具。CFD用于研究气体和流体流动现象时，不需要物理装置，成本较低，且具有对于大多数物理现象可以模拟，只需一次模拟就可以收集大量的数据的优势。目前，CFD在跳台滑雪方面已有一些应用研究。

跳台滑雪服一直是跳台滑雪气动特性的讨论焦点。由于跳台滑雪服设计解决方案越来越巧妙，增加了跳台滑雪服的空气动力效应，有时甚至超出了规则的范围，从而使其可能成为监管最严格的运动装备之一。从以往的宽松跳台滑雪服向现代的贴身跳台滑雪服的转变也存在一些问题。最大的问题在于硬跳台滑雪服材料不允许身体部分的平稳运动，而更易拉伸的跳台滑雪服材料可以消除这一问题，但会大大降低空气动力学。一个值得研究的解决方案是增加滑雪板的宽度，以便补偿上述因使用贴身滑雪服产生的气动力效应损失。

户外现场环境因素主要包括风环境和气压环境，在跳台滑雪过程中是不可忽视的。因此，有理由相信，风环境与气压环境对气动特性以及稳定性的影响研究可能成为跳台滑雪空气动力学领域未来的研究热点。

智能化风洞实验训练馆必定是未来跳台滑雪空气动力学研究的重要工具，将广泛用于户外现场环境的模拟、气动力测量、运动员技术动作辅助训练以及运动装备优化设计实验研究等方面。

[1] 陈志峰. 跳台滑雪运动空中飞行阶段的CFD研究[J]. 浙江体育科学, 2014, 36(2): 121-124.

[2] 刘树明. 跳台滑雪飞行姿势及其技术的优化[J]. 沈阳体育学院学报, 2002, 21(2): 22-24.

[3] 王志选, 李润, 关佐恒, 等. 跳台滑雪空中飞行初始姿态的实验研究[J]. 体育科学, 1998, 18(2): 1-5.

[4] CHARDONNENS J, FAVRE J, CUENDET F,. Measurement of the dynamics in ski jumping using a wearable inertial sensor-based system[J]. J Sports Sc, 2014, 32(6): 591-600.

[5] CHOWDHURY H, ALAMA F, MAINWARING D. Aerodynamic study of ski jumping suits[J]. Procedia Eng, 2011, 13: 376-381.

[6] CUTTER D A. Nordic Ski Jumping Aerodynamics[M]. AIAA, Aeronautical Engineering, United States Air Force Academy, CO: Colorado Springs, 1993.

[7] DENOTH J, LUETHI S M, GASSER H. Methodological problems in optimisation of the flight phase in ski jumping[J]. Int J Sport Biomech,1987, 3: 404-418.

[8] ETTEMA G, BRATEN S, BOBBERT M F. Dynamics of the in-run in ski jumping: a simulation study[J]. J Appl Biomech, 2005, 21: 247-259.

[9] ETTEMA G, HOOIVELD J, BRATEN S,. How do elite ski jumpers handle the dynamic conditions in imitation jumps?[J]. J Sports Sci, 2015, 34(11):1081-1087.

[10] FIS. Specifications for competition Equipment and commercial markings[EB/OL].http://www.fis-ski.com/mm/Document/documentlibrary/Marketing/04/30/53/Competitionequipment_1617_11072016_clean_English.pdf .

[11] FIS Fact Sheet. Important new rules in ski jumping and nordic combined summer grand prix[EB/OL]. http://www.fis-ski.com/mm/Document/document/General/04/23/02/July292009NewrulesatSkiJumpingandNordicCombinedSummerGrandPrix2009_Neutral.pdf.

[12] GARDAN N, SCHNEIDER A, POLIDORI G,. Numerical investigation of the early flight phase in ski-jumping[J]. J Biomech, 2017, 59(1): 29-34.

[13] GROZIN E A. Ski-jumping [M]. Moscow：Phyzcultura i sport, 1971.

[14] JIN H, SHIMIN S, WATANUKI T,. Desirable gliding styles and techniques in ski jumping[J]. J Appl Biomech,1995, 11: 460-474 .

[15] JOST B. Differences in some kinematic flight parameters between the classical and the new so called “V” technique in ski jumping[J]. Kinesiology, 1994, 26(1-2): 18-21.

[16] JUNG A, STAAT M, MULLER W. Flight style optimization in ski jumping on normal, large, and ski flying hills[J]. J Biomech, 2014, 47(3): 716-722.

[17] KEIZO Y, MAKOTO T, JUN I,. Effect of posture on the aerodynamic characteristics during take-off in ski jumping [J]. J Biomech, 2016, 49(15): 3688-3696.

[18] MAHNKE R, HOCHMUTN G. Neue Erkenntnisse zur Luftkraftwirkung beim Ski-springen[C]. Research Report for Forschungsinstitut für Körperkultur und Sport, Leipzig, 1990: 45-49.

[19] MARQUES-BRUNA P, GRIMSHAW P. Mechanics of flight in ski jumping: aero-dynamic stability in pitch[J]. Sports Technol, 2009, 2(1-2): 24-31.

[20] MARQUES-BRUNA P, GRIMSHAW P. Mechanics of flight in ski jumping: aero-dynamic stability in roll and yaw[J]. Sports Technol, 2009, 2(3-4): 111-120.

[21] MARYNIAK J, KRASNOWSKI B. Balance and longitudinal stability of a ski jumper in flight [J]. Mechanika Teoretyczna I Stosowana, 1974, 2(3): 351-373.

[22] MARYNIAK J, LADYZYNSKA-KOZDRAS E, TOMCZAK S. Configurations of the Graf-Boklev (v-style) ski jumper model and aerodynamic parameters in a wind tunnel[J]. Hum Mov, 2009, 10(2): 130-136.

[23] MEILE W, REISENBERGER E, MAYER M,. Aerodynam-ics of ski jumping: experiments and CFD simulations[J]. Exp Fluids, 2006, 41(6): 949-964.

[24] MULLER W. Determinants of ski-jump performance and implications for health, safety and fairness[J]. Sports Med, 2009, 39(2): 85-106.

[25] MULLER W. Performance factors in ski jumping[J]. J Biomech, 2006, 39(1): 192-213.

[26] MULLER W. Towards research-based approaches for solving body composition problems in sports: ski jumping as a heuristic example[J]. Br J Sports Med, 2009, 43: 1013-1019.

[27] MULLER W, GROSCHL W, MULLER R,. Underweight in ski jumping: The solution of the problem[J]. Int J Sports Med, 2006, 27(11): 926-934.

[28] MULLER W, PLATZER D, SCHMOLZER B. Dynamics of human flight on skis: improvements in safety and fairness in ski jumping[J]. J Biomech, 1996, 29(8): 1061-1068 .

[29] MULLER W, PLATZER D, SCHMOLZER B. Scientific approach to ski safety[J]. Nature, 1995, 375(6531): 455-466.

[30] MURAKAMI M, IWASE M, SEO K,. High-speed video image analysis of ski jumping flight posture[J]. Sports Eng, 2014, 17(4): 217-225.

[31] MURAKAMI M, IWASE M, SEO K,. Ski jumping flight skill analysis based on high-speed video image[J]. Procedia Eng, 2010, 2(2): 2381-2386.

[32] NØRSTRUD H. Alpine downhill and speed-skiing[J]. Sport Aerodyn,2008, 506: 131-138.

[33] NØRSTRUD H, ØYE I J. On CFD simulation of ski jumping[J]. Comput Fluid Dynamics Sport Simulat, 2009, 72(1): 63-82.

[34] REMIZOV L P. Biomechanics of optimal flight in ski-jumping[J]. J Biomech, 1984, 17(3): 167-171.

[35] SCHMOLZER B, MULLER W. Individual flight styles in ski jumping: results obtained during Olympic games competitions[J]. J Biomech, 2005, 38(5): 1055-1065.

[36] SCHMOLZER B, MULLER W. The importance of being light: aerodynamic forces and weight in ski jumping[J]. J Biomech, 2002, 35(8): 1059-1069.

[37] SCHWAMEDER H. Biomechanics research in ski jumping: 1991-2006[J]. Sport Biomech, 2008, 7(1): 114-136.

[38] SCHWAMEDER H, MULLER E. Biomechanische besreibung und analyse der V-Technik im skispringen[J]. Spectrum der Sportwissenschaften, 1995, 7: 5-36.

[39] SEO K,. Aerodynamic study for the ground effect of ski jumping[C]. San Francisco：19thISBS Conference, 2001: 128-130.

[40] SEO K, MURAKAMI M, YOSHIDA K. Optimal flight technique for V-style ski jumping[J]. Sports Eng, 2004, 7(2): 97-104.

[41]SEO K, WATANABE I, MURAKAMI M. Aerodynamic force data for a V-style ski jumping flight[J]. Sports Eng, 2004, 7(1): 31-39.

[42] STRAUMANN R. Vom Skisprung zum Skiflieg[J]. Sport, 1955: 7-8 .

[43] STRAUMANN R. Vom Skiweitsprung und seiner Mechanik, in Jahrbuch des Schweize-rischen Ski Verbandes[J]. Selbstverlag des SSV, 1927: 34-64.

[44] TANI I, IUCHI M. Flight mechanical investigation of ski jumping[M]// Scientific Study of Skiing in Japan, 1971: 35-52

[45] TAVERNIER M, COSSERAT P. Flight simulation of ski-jumping comparison of two styles of flight[C]. Paris:14th Congress of ISB Congress, 1993: 1328-1329.

[46] THOMPSON B E, FRIESS W A, KNAPP K N. Aerodynamics of speed skiers[J]. Sports Eng, 2001, 4: 103-112.

[47] VIRMAVIRTA M. Aerodynamics of ski jumping[M]// MÜLLER B, WOLF S I. Handbook of Human Motion. New York : Springer, 2017: 1-21.

[48] VIRMAVIRTA M. Aerodynamics of ski jumping[M]// BRAGHIN F,. The Engineering Approach to Winter Sports. New York: Springer,2016: 153-181.

[49] VIRMAVIRTA M, ISOLEHTO J, KOMI P,. Characteristics of the early flight phase in the Olympic ski jumping competition[J]. J Biomech, 2005, 38(11): 2157-2163.

[50] VIRMAVIRTA M, KIVEKAS J. Aerodynamics of isolated ski jumping ski[C]. Glasgow: XXV ISB Congress, 2015: 215-223.

[51] VIRMAVIRTA M, KIVEKAS J. Effective use of a wind tunnel for ski jumping suit research[C]. Cape Town:XXIIth ISB Congress, 2009: 176-188.

[52] VIRMAVIRTA M, KIVEKAS J. Is it still important to be light in ski jumping?[C]. Natal:XXIV ISB Congress, 2013:347-360 .

[53] VIRMAVIRTA M, KIVEKAS J. The effect of wind on jumping distance in ski jumping - fairness assessed[J]. Sport Biomech, 2012, 11(3): 358-369

[54] VIRMAVIRTA M, KIVEKAS J, KOMI P V. Ski jumping take-off in a wind tunnel with skis[J]. J Appl Biomech,2011, 27(4): 375-379 .

[55] VIRMAVIRTA M, KIVEKAS J, KOMI P V. Take-off aerodynamics in ski jumping[J]. J Biomech, 2001, 34: 465-470.

[56] VIRMAVIRTA M, KOMI P V. Measurements of the take-off forces in ski-jumping Part I and II.[J]. Scand J Med Sci Sports, 1993, 3: 229-243.

[57] WARD-SMITH A J, CLEMENTS D. Experimental determination of the aerodynamic characteristics of ski-jumpers[J]. Aeronaut J,1982, 86: 384-391.

[58] WARD-SMITH A J, CLEMENTS D. Numerical evaluation of the flight mechanics and trajectory of a ski-jumper[J]. Acta Appl Math, 1983, 1(3): 301-314.

[59] WATANABE K, WATANABE I. Aerodynamics of ski-jumping: effect of ‘Vstyle’ to distance[C]. XIVth Congress of the International Society of Biomechanics, 1993: 1452-1453.

A Review of Aerodynamics Research in Ski Jumping

HU Qi1, ZHANG Wen-yi2, CHEN Qi1

1. China Institute of Sport Science, Beijing 100061, China; 2. Beijing Sport University, Beijing 100084, China.

Ski jumping performance involves ballistic and aerodynamic factors, which primarily determine the research requirements of the winter sport. Ski jumper’s velocity and position of the body center of mass at the release instant from the take-off table quantify the flight trajectory and the length of the jump. Aerodynamic factors cover all aspects of aerodynamic characteristics of the jumper/skis system. Ski jumping performance is often divided into four different phases: in-run, take-off, flight, and landing. In this paper, aerodynamic research results involved in different phases of ski jumping have been discussed and reviewed, in which a good mixture of wind tunnel measurements, computer simulations and field studies has been used mostly. Aerodynamics plays important role during each of these phases and the flight phase has been studied most. The flight style has experienced the transformation from the classic vertical style to the V-style. The position during in-run phase ia the key to reduce aerodynamic drag and increase inrun speed. Take-off and its subsequent transition into flight phase are considered the most important phases as they determine jumper’s initial conditions and final position during the flight. The attitude of athlete/skis system is very important to aerodynamic characteristics, where the equipment (skis and suits), weight and wind have a big role as well in flight phase. Ground lift effect willbeen seen in landing phase with V-style. In addition, it is suggested that attention should be paid to the skis’ posture and structural parameters, and outdoor environment in aerodynamics research in ski jumping. Meanwhile, the developing direction in future could be computational fluid dynamics (CFD) and intelligent wind tunnel experimental and training venue.

1002-9826(2018)05-0132-08

10.16470/j.csst.201805021

G863.12

A

国家自然科学基金资助项目(11802068); 国家体育总局体育科学研究所基本科研业务费资助项目(基本18-29); 中央高校基本科研业务费专项资金资助项目(2018RC016)。

胡齐,男,助理研究员,主要研究方向为体育工程、流体与机械工程、运动生物力学, E-mail: huqi@ ciss.cn。