基于Weibull分布函数的等离子喷涂涂层接触疲劳寿命预测

费晓瑜, 李国禄, 王海斗

（1．天津职业大学 机电工程与自动化学院，天津 300410；2．河北工业大学 材料科学与工程学院，天津 300130；3．装甲兵工程学院 装备再制造技术国防科技重点实验室，北京 100072）

接触疲劳失效是很多机械零部件（如轴承、齿轮、机车车轮、轮轨等）的主要失效模式，该失效起源于工件表面或次表面层的塑性变形而引起的疲劳损伤，表面工程技术能有效地提高接触区域内的抗疲劳磨损能力，延长工件使用寿命，节约制造成本[1]。等离子喷涂技术作为一种表面修复和改性技术，已被成功应用于工件表面的耐磨、耐蚀、耐疲劳等处理，为产品的再制造提供了一个有效的手段[2-5]。Ni基合金不仅具有优良的耐热、耐磨、耐疲劳性能，而且特别适用于等离子喷涂技术，得到了广泛的研究与应用[6-9]。

在对接触疲劳寿命的研究过程中发现，由于超音速等离子喷涂方法本身的特点，涂层中不可避免地存在微孔隙、微裂纹、氧化夹杂及未融粒子等缺陷[10]，造成疲劳寿命较为离散；另外，超音速等离子喷涂NiCrBSi涂层具有较高的接触疲劳寿命，实验时间成本较高；所以，通过科学的数学统计方法建立接触疲劳寿命模型尤为重要。Weibull分布和正态分布是最常用的处理和分析疲劳寿命的统计方法，张志强等[11]使用正态分布对涂层接触疲劳寿命进行了分析，并采用统计分析方法对寿命数据进行了讨论。然而，在Weibull分布对涂层接触疲劳寿命的研究中，众多学者只建立了Weibull分布模型，并未进行多元统计分析。本工作采用超音速等离子喷涂技术制备NiCrBSi合金涂层，对涂层性能进行分析，通过Weibull分布函数对不同载荷条件下涂层的接触疲劳寿命进行统计分析，并通过巴特利特检验和F检验对Weibull函数以及载荷对接触疲劳寿命的影响进行分析讨论。

1 实验

1.1 涂层制备

采用HEPJet高效能超音速等离子喷涂设备在45钢基体上制备NiCrBSi合金涂层，设备最大功率为80 kW，液滴冲击速度达到400～600 m/s[12]。喷涂基材45钢，加工为内径30 mm、外径60 mm、高度25 mm、内外孔处倒角为45°的圆环试样，两端面及内孔均磨光处理，表面粗糙度Ra值0.8 μm。喷涂材料NiCrBSi合金粉末成分（质量分数/%）为：Cr 15.8，B 3.1，Si 4.5，Fe 5，C 0.8，余量 Ni。粉末形貌如图1所示，粉末颗粒为球状，球化程度良好，具有较好的流动性，利于喷涂。为提高涂层的结合强度，喷涂前用丙酮清洗基体，并用棕刚玉喷砂处理，得到粗糙的金属表面，之后先喷涂Ni/Al粉末打底，成分（质量分数/%）为：Ni 90，Al 10。通过喷涂Ni/Al粉末形成的微熔池效应，提高涂层与基体的结合强度[13]，随后进行NiCrBSi粉末的喷涂，喷涂工艺参数见表1，其中氩气为主气，氢气为辅气，氮气为送粉气。喷涂厚度约为400～500 μm。喷涂完成后，对涂层表面进行打磨、抛光处理，处理后涂层厚度约为350 μm，表面粗糙度Ra约为0.2 μm。

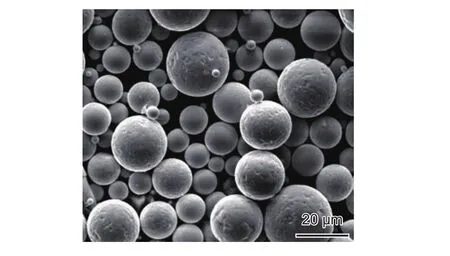
图 1 NiCrBSi合金粉末形貌Fig. 1 Morphology of NiCrBSi alloy powder

表 1 喷涂工艺参数Table 1 Plasma spraying parameters

1.2 接触疲劳寿命实验

采用YS-1型球盘式接触疲劳试验机，对涂层的抗接触疲劳性能进行测试，试验机见文献[14]。实验在充分油润滑的条件下进行，轴承球材料为GCr15钢，表面粗糙度为0.012 μm，硬度为60HRC。转速设定为1500 r/min，载荷分别为50 N，100 N，150 N，200 N，250 N，通过振动信号判断涂层失效，当振幅信号连续超过临界值（5 g）时，即判定涂层失效，涂层失效的SEM照片如图2所示，可以看到较为明显的涂层剥落。每次实验结束后，更换轴承，以保证实验精确。每种载荷条件，进行7次平行实验，实验得到不同载荷下涂层的接触疲劳寿命见表2。

2 涂层性能及接触疲劳寿命表征

2.1 涂层性能表征

图3为涂层截面的SEM照片，可以看到，涂层整体结构致密，存在少量孔隙和微裂纹。采用灰度法[15]对涂层的孔隙率进行测量，得到涂层的孔隙率为1.36%。通过X射线应力衍射仪测得涂层的残余应力为拉应力，大小为+213 MPa。

2.2 接触疲劳寿命表征

采用两参数Weibull分布来处理接触疲劳实验数据，并通过Weibull失效概率曲线图来表征涂层的寿命。Weibull分布是最常用的疲劳寿命数据统计分布之一，具有适用性广、覆盖性强的特点，其分布函数为[16]：

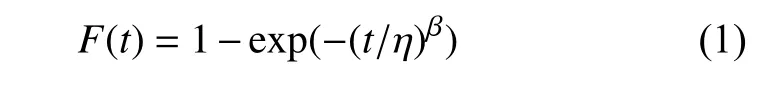
式中：F（t）为t次循环的失效概率，η为位置参数，即疲劳寿命，β为形状参数，即Weibull曲线的斜率。

图 2 涂层表面失效形貌Fig. 2 Surface failure morphology of coating

2.2.1 范-蒙特福特检验

通过范-蒙特福特检验法验证寿命数据是否符合Weibull分布[17]，建立如下假设：

H0：产品的寿命分布服从 Weibull分布 W（β, η）

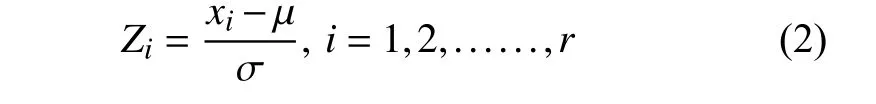
为检验H0，范-蒙特福特提出统计量：

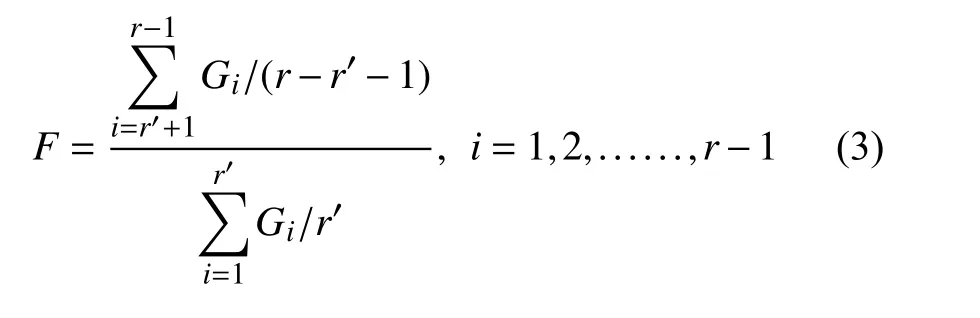
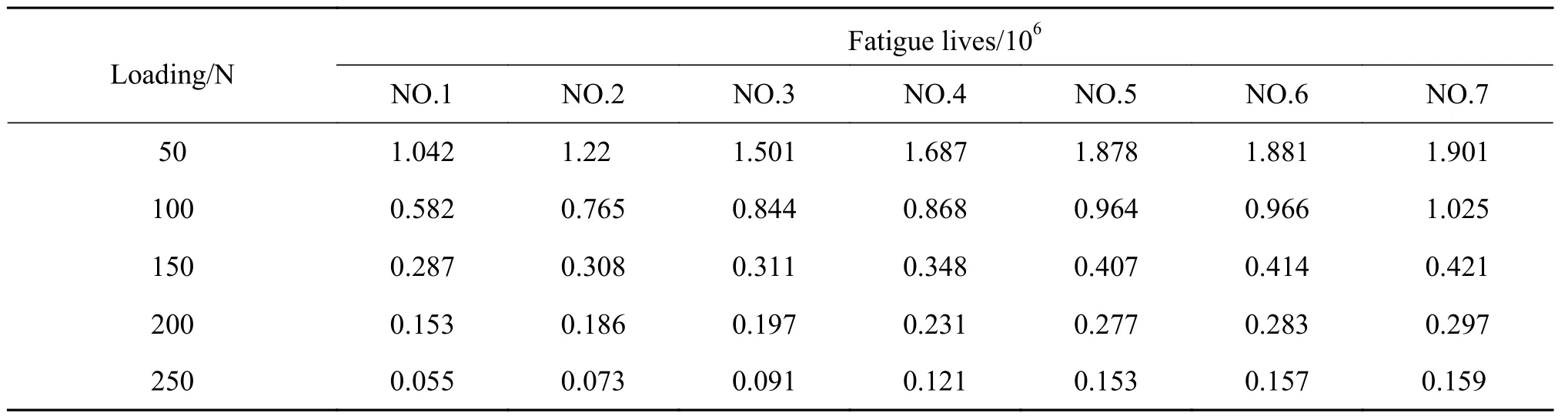
表 2 不同载荷下涂层的接触疲劳寿命Table 2 RCF experimental results under five kinds of loading condition

图 3 NiCrBSi涂层截面微观结构形貌Fig. 3 Cross-section microstructure of NiCrBSi coating

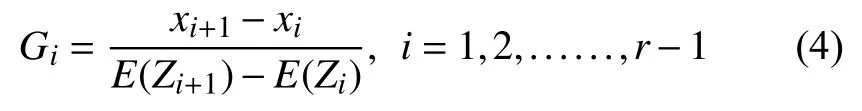
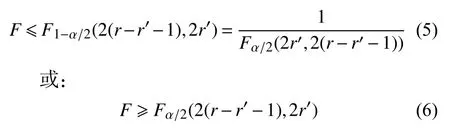
则认为假设不成立，否则可以认为该样本符合Weibull分布。

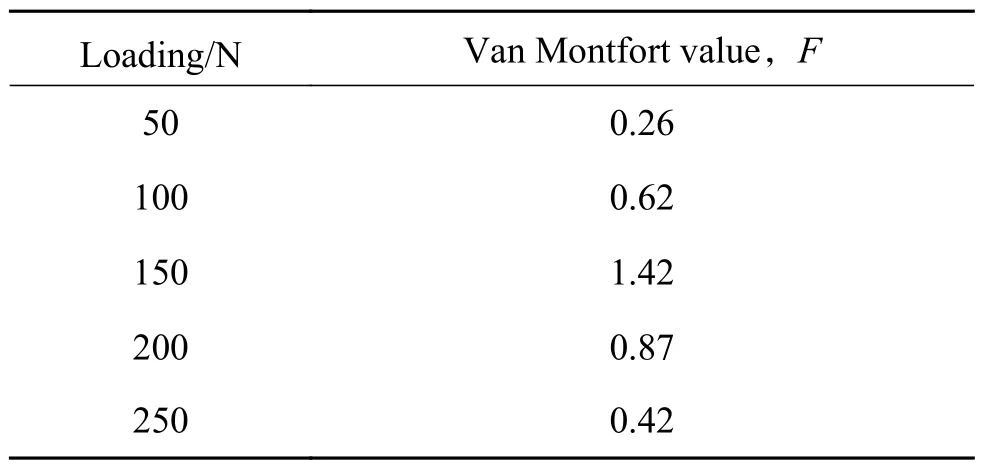
表 3 不同载荷下F的计算值Table 3 Van Montfort value (F) under five kinds of loading condition

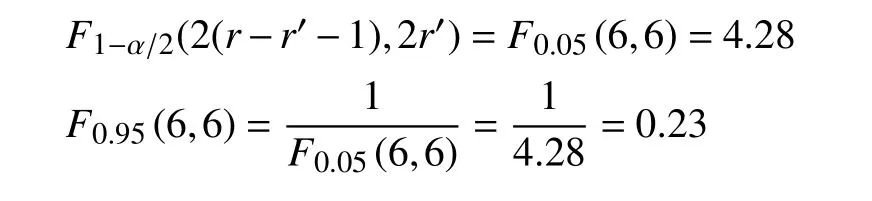
五种不同载荷条件下，F的计算值均介于F0.95（6，6）和 F0.05（6，6），所以不能拒绝假设条件H0，即产品寿命服从Weibull分布。

2.2.2 最好线性无偏估计

用精度较高且使用简便的“最好线性无偏估计法（BLUE）”来计算Weibull分布的两个参数β，η，令参数μ和σ的BLUE公式如下[15]：

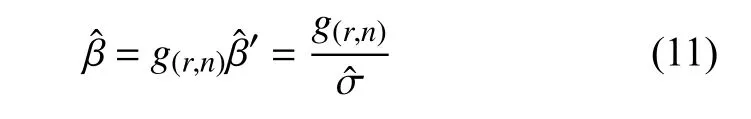
计算结果如表4所示。

根据式（1）建立Weibull失效概率图，用以表征涂层的接触疲劳寿命，如图4所示。通过图4，可以直观得到在同一工作条件下，涂层任意循环次数的失效概率，也可用于某一工作条件下涂层接触疲劳寿命的预测。

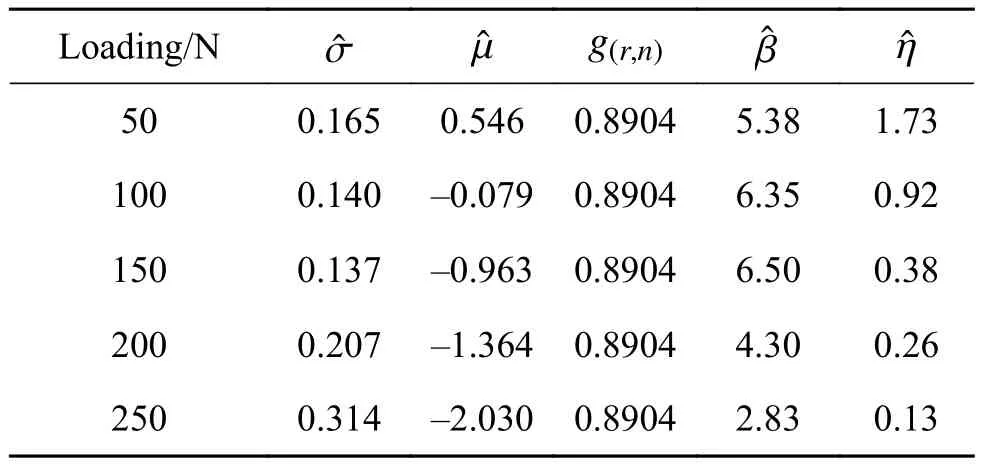
表 4 5种载荷下参数μ和σ的BLUE估计值Table 4 BLUE value of μ & σ under five kinds loading condition

3 载荷条件与疲劳寿命的相关性分析

用接触疲劳特征寿命即失效概率为63.2%时的寿命作为涂层的疲劳寿命。根据特征寿命与载荷条件之间的散点图，假设疲劳寿命与载荷符合指数模型即接触疲劳特征寿命的对数与载荷符合一元回归模型，利用EXCLE回归分析模块功能求解得到：

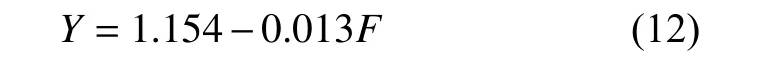
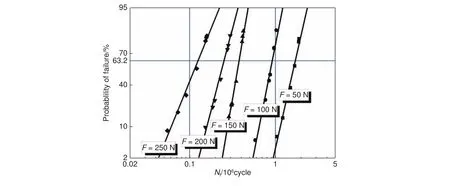
图 4 5种载荷条件下涂层的Weibull失效概率曲线图Fig. 4 Weibull failure probability curve under five kinds of loading condition

可决系数R2=0.989，即接触疲劳特征寿命变化的98.9%由载荷条件的变化所决定，拟合优度非常高，特征寿命的对数与载荷的拟合曲线如图5所示。得到疲劳特征寿命与载荷之间的回归模型为：拟合曲线如图6所示。

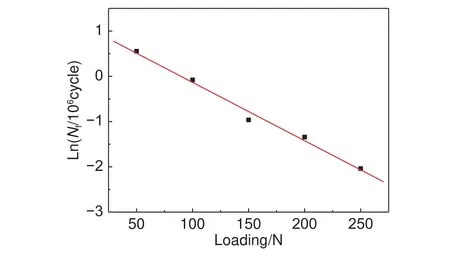
图 5 特征寿命的对数与载荷的拟合曲线Fig. 5 Fitted curve between Ln (Nf) and loading

4 结论

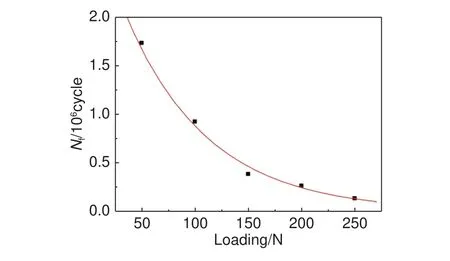
图 6 特征寿命与载荷的拟合曲线Fig. 6 Fitted curve between Nf and Loading

（1）采用超音速等离子喷涂技术制备的NiCrBSi合金涂层整体结构致密，仅存在少量孔隙和微裂纹，残余应力较小，总体性能较为优异。

（2）通过范-蒙特福特检验法验证涂层接触疲劳寿命数据符合Weibull分布，建立的Weibull概率分布图可在实验数据较少的情况下，精确表征涂层的接触疲劳寿命。

（3）建立了接触疲劳特征寿命及其对数与载荷之间的指数回归模型，以及接触疲劳特征寿命的对数与载荷之间的线性回归模型，并通过可决系数法进行了验证。回归模型可对一定范围内任意载荷条件下涂层的接触疲劳寿命进行预测。