全国非泵送混凝土回弹值的统一测强回归方程拟合及检验
2018-10-09阚洪弟
阚 洪 弟
(山东华材工程检测鉴定有限公司,山东 济南 250082)
1 概述
在混凝土体结构的强度检测方法中,回弹法由于其可在平整、光洁的结构外表面直接进行检测(而无需像钻芯法那样要对内部先剔凿再检测),检测过程简单、方便、快速、不干扰正常使用,并且无破坏(准确讲,应为半破坏,因为回弹法锤击结构表面,只对物体表面产生损伤或破坏),检后几乎无需修复等一系列突出优点,使其虽因其精度受到质疑(比如文献[1]第4.3.2条第5款指出,回弹法宜进行钻芯修正或室内试块抗压强度修正),但在还没有出现更好的高精度、快捷又兼具无破坏的检测方法问世之前,仍是目前各检测机构最常用到的主要检测方法之一。
目前,对于行标JGJ/T 23—2011回弹法检测混凝土抗压强度技术规程(以下简称“规程”或干脆省略)附录A[2]中全国非泵送混凝土强度只有与回弹值、碳化深度之间的对照表,而没有具体表达式、不便于自动化运算的状况,张石柳[3]和董振忠[4]分别用Excel和EXCEL VBA软件编制了自动计算表格,方便了运算。由于各地都建立了更适合于本地区的地方规程,且随着非泵送混凝土使用的减少,专门针对非泵送混凝土建立的拟合公式就很少。本文针对“规程”附录A所建立的拟合公式及各种统计分析方法,最主要的是提供了一种分析模式或范式,且这种范式对方差服从正态分布的多元线性回归模型是普遍适用的。
2 回归方程的拟合
首先按照“规程”第E.0.4条第2款中如下形式的回归方程:
(1)
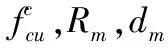
先对式(1)变形:
令:
得到二元(p=2)线性回归模型如下:

其中,上角标(1),…,(n)代表第1,…,n次测试数据。考虑到测试数据的总体递变规律,我们已经对不符合递变规律的如下数据组进行了剔除:
这样,总有效数据点数n=2 146。那么参数矩阵B的最佳拟合值为[6]:
如此,式(1)中所需拟合的参数最佳拟合值为:
这样就得到了没有修正的,即回弹仪垂直弹击混凝土体侧表面时的全国非泵送混凝土统一测强回归曲线如下:
(2)

引用2节中数据σ,c11,c22,取置信水平α=0.05,回归系数的置信区间[8]分别为:
3 回归方程和回归系数的显著性检验
回归方程和回归系数的显著性检验所用到的主要公式[7]如下:
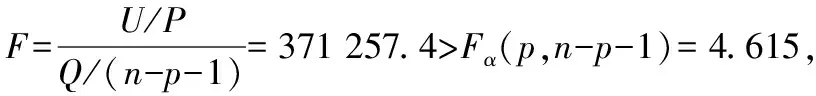
4 误差分布的检验
2)采用D检验法[8]。
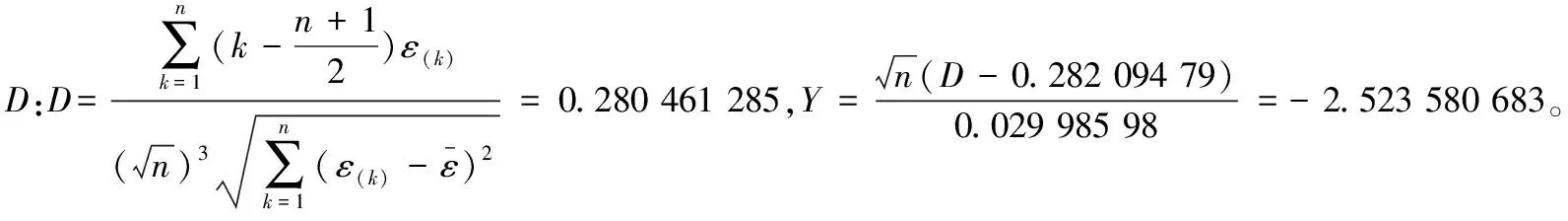
其中,Y为D的标准化变量。因Y不在区间(Zα/2,Z1-α/2)=(-2.91,2.25)之内(取显著性水平α=0.01),故也认为ε服从正态分布。
3)采用柯尔莫哥洛夫检验法[8]。
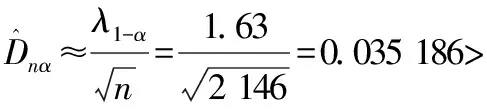
三种检验方法均证明:误差ε确系服从正态分布。
5 考虑交互作用的双因素方差分析
利用公式[6]:
如下结算结果表明:因素A、因素B、交互作用A×B对强度值都有高度影响(取显著性水平α=0.01)。
随着离差值2Δ变大,因素A与因素B之间的交互作用减弱,当交互作用消失时所对应的离差值2Δcr称为临界离差。表1列出固定水平Ai,Bj,只有强度值Xijk变动的情况下,Xijk服从不同分布规律时的临界离差。另外,若取文献[5]中表1数据,可以直接计算Rm与dm之间的相关系数矩阵R=(rij),反映Rm与dm之间的相关系数r12=-0.179≠0(有趣的是,其与x1与x2之间的相关系数r12=-0.175近似相等),说明二者确实具有较明显的相关关系。


表1 几种测强数据分布所对应的临界离差对照表 MPa
6 给定置信限下的预测区域
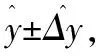
比如新测点(Rm,dm)=(40,2.0),则x=(1,x1,x2)=(1,logRm,dm)=(1,1.602 06,2.00)),计算得:


7 结论

2)指出回归方程拟合过程中,中间结果宜保留较多位数,不应每一步都按有效数字位数规则取舍。

4)例示了如何由一个实测点/一组实测点,得到给定置信系数下的预测区间/预测区域。
