基于李雅普诺夫函数的电磁轴承电压控制
2018-10-09刘学平
朱 戡,刘学平
(清华大学深圳研究生院先进制造学部,广东深圳 518000)
磁悬浮轴承(AMB)可以提供非接触式的支撑力,避免了摩擦、润滑之类的问题,可以达到很高的转速,因此在很多方面得到了应用[1-3]。
随着电磁轴承在工业中日益广泛的运用,在转子跨度较大的轴承中,往往采用柔性转子的设计[4]。当转子穿越临界转速时,由于不平衡质量等因素的影响,往往会产生较大的振动幅值,甚至会导致运动失稳,因此,转子振动控制与稳定性研究一直是国内外研究的热点[5-7]。
面对非线性电磁力,最早的线性化模型是Schweitzer.G[8]提出,后来为实现较大范围的线性化,陆续又出现许多控制方法[9-10]。Cui Peiling[11]等将滑模观测器与陷波器相结合,有效减小陀螺转子所受的同频轴承力。Han Bangcheng[12]等通过建立电磁轴承不平衡力模型,采取插入式重复控制器降低转子的振幅。Arkadiusz Mystkowski[13]等面对非线性电磁轴承系统,采用反馈线性化方法对系统进行控制。M.Kamel[14]等考察具有非线性恢复力的Jeffcott转子振动情况,并利用非线性PD控制器有效抑制转子的振动。A.Al-Mandouh[15]等研究具有时变刚度的电磁轴承,并设计一种非线性延时控制器。
随着各种控制方法在电磁轴承控制上的应用,李雅普诺夫方法也逐渐被引入。Li Guodong[16]等针对单自由度的转子,构建李雅普诺夫函数,实现大范围内转子的平衡。Isao TAKAMI[17]则利用李雅普诺夫理论,通过线性分式变换构建增益调度控制器,Tao Zhang[18]研究由于由传感器漂移导致的同步周期扰动对转子振动的影响,并利用李雅普诺夫方法设计控制器,有效抑制系统的谐波干扰,并保证系统的大范围渐进稳定性。但是这些研究对象都是刚性转子,没有考虑到柔性转子在越过临界转速时所面对的问题。
本文作者针对柔性转子在临界转速会产生大范围振动的问题,结合李雅普诺夫函数,设计一种基于能量的控制方法,使得柔性转子在跨越临界转速时,能够有效抑制振动,并通过仿真进行验证。并通过调整参数,研究不同控制参数对系统响应性能的影响。
1 电磁轴承模型
1.1 柔性转子建模
转子由1根轴和4个具有不平衡质量的圆盘组成。如图1所示,4个圆盘均匀分布在轴上,其中2个处在轴端;转子由2个电磁轴承支撑。转子正中心为P1,转子边缘处为P2。为了简化问题,转子设置为完全对称,不平衡质量集中分布在4个圆盘上。转子的各项参数如表1所示。
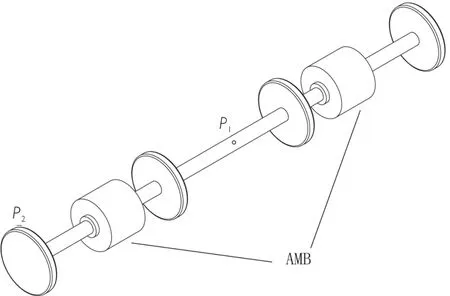
图1 电磁轴承柔性转子Figure1 flexible rotor in AMB
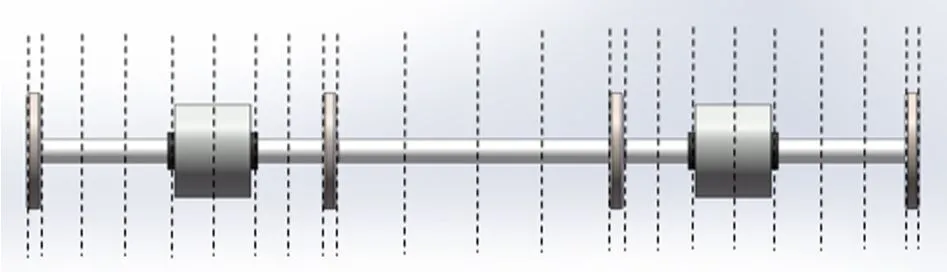
图2 转子有限元模型Figure 2 FEM of the rotor
转子的动力学模型为:

式中:M、G、K分别是转子的质量矩阵、阻尼矩阵和刚度矩阵,G=C+ωJ,J是由陀螺力矩产生的矩阵。x是转子的位置向量,F是转子所受到的广义力,包括了电磁铁所施加的电磁力和转子质量不平衡所导致的离心力。
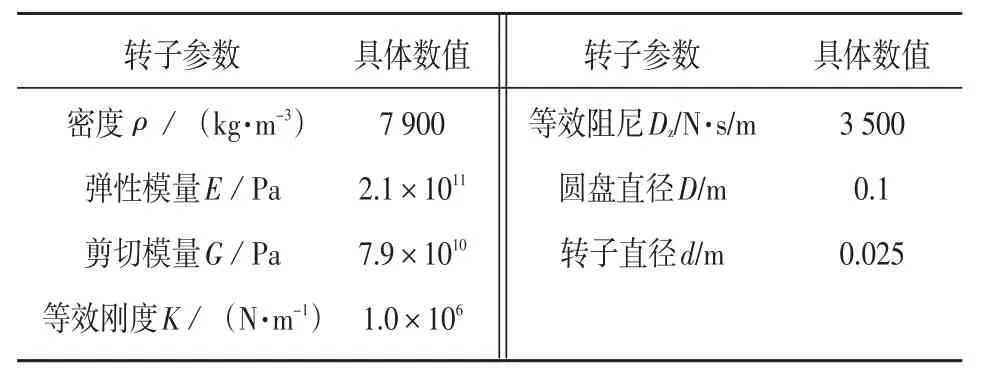
表1 转子与电磁轴承部分参数Tab.1 Parameters of the rotor and AMBs
将转子划分为19个单元,其中4个转盘采用圆盘单元,转轴采用铁摩辛柯梁单元进行建模,如图2所示。在给定的等效刚度和阻尼下,经过计算,可以得到转子的坎贝尔图。转子的一阶临界频率为204.5 Hz(ω=1 285rad/s),二阶临界转速为565 Hz。当转子处于一阶临界转速时,转子的最大振动位移处于转轴边缘位置(P2),其幅值约为1.5 mm,如图3所示。
磁悬浮轴承线圈中电流与电压有如下关系[19]:

式中:R是电阻,L是电感,ki等于力-电流因子。
由于在电磁轴承中,除了转子的位移和速度外,绕组电流也是一个系统状态量,会影响系统总体性能,因此,将位移x,速度ẋ和线圈电流q̇设为状态变量,令:

利用式(3),采用电压控制来设计电压u的值,可以实现转子状态的控制。
1.2 电磁力
通常的电磁轴承中采用差动模式,作用在转子上的电磁力可以表示为位移和电流的函数[1,8]:
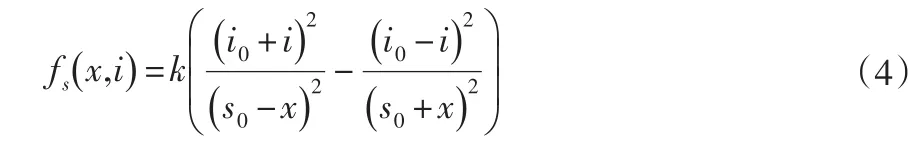
式中:i0和s0分别为偏置电流和最大气隙。,μ0为真空磁导率,n为线圈匝数,A为气隙横截面积。
当x<<s0时,利用泰勒展开并消去高次项,可以得到线性化模型:
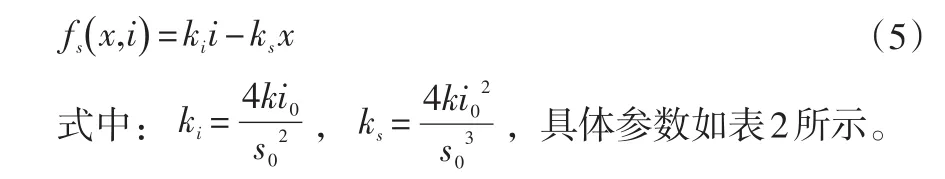
2 基于能量的电压控制
整个电磁轴承系统的能量可以分为电磁能E1、转子的动能E2和势能E3。转子的势能由重力势能和转子变形引起的弹性势能组成,由于转子的变形较小,忽略其弹性势能,并将转子平衡位置设为势能零点。可得三者能量:

当转子稳定悬浮时,为简化问题,将转子视为一个刚性单自由度转子,定义拉格朗日函数T=E1+E2-E3,则利用拉格朗日-麦克斯韦方程可以得到整个系统的动力学方程[20]:
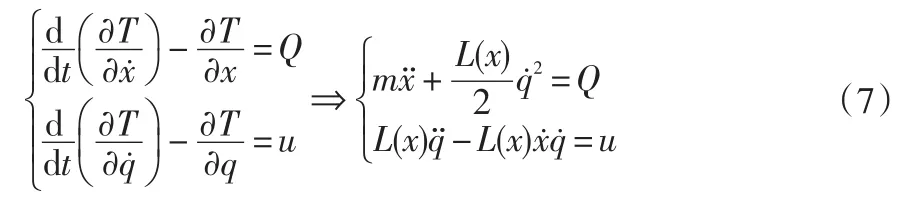
式中:x、q是位移和电荷,Q是广义力,包括转子的重力和离心力。u是线圈电压。
总能量E=E1+E2+E3。当转子稳定悬浮时,系统的电磁能,动能 E͂和重力势能 E͂都为 0,则二者23的差值 ΔE͂=E-E͂。
构造李雅普诺夫函数:
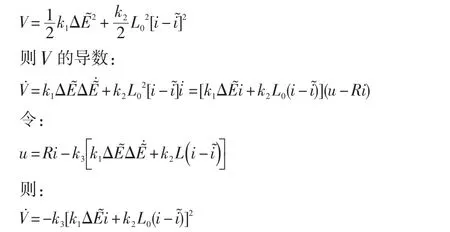
只要k1、k2、k3的值为正数,则V>0,V̇<0,由李雅普诺夫定理可知,此时以x、ẋ、q为状态变量的磁悬浮转子系统是大范围渐进稳定的,因此可以使转子在大范围内保持稳定。由电压项的控制律可以看出,k1是电磁轴承整体的能量项系数,k2是电流的修正项系数,k3是电压放大倍数,改变以上3个参数,可以改变最终得到的电压构成,从而可以得到良好的响应。
3 仿真结果与分析
3.1 跨越临界转速时的响应
当转子处于一阶临界转速附近时,采用传统PID控制(P=7 500 A/m,D=12.3 A·s/m)和基于能量的李雅普诺夫控制(k1=k2=k3=1)所得到的转子振动位移如图4所示。
从图中可以看出,当转子处于一阶临界转速附近时,基于李雅普诺夫函数的能量控制控制下的柔性转子的稳态振动幅值明显小于PID控制下的稳态振动幅值。当转速ω=1 275rad/s时,振动幅值约下降15%,ω=1 290rad/s时,振动幅值下降大约38%。响应时间方面,PID控制约在1.5 s左右达到稳态,电压控制在0.5 s左右基本达到稳态,较大提升系统的响应速度。
另一方面,基于李雅普诺夫函数的电压控制系统的震荡频率较大。从图4中可以看出,在系统从初始状态到稳态的过程中,电压控制的上升过程伴随着较大的抖动,而PID控制的系统上升过程平滑,基本没有出现高频率的抖动。因此,电压控制虽然提升了系统的响应时间,降低了转子在稳态条件下的振动幅值,但是牺牲了部分动态性能。
3.2 不同参数对电磁轴承响应的影响分析
经过仿真分析,调整不同的控制参数(k1,k2,k3),并不会改变系统的稳态响应,但是会明显影响到系统的动态特性。如图5所示,随着k1,k2,k3的变化,系统的动态性能差异较大。k1=4,k2=1,k3=0.1时,系统的超调量较大,但响应速度较快,k1=8,k2=64,k3=0.1时,系统超调量得到抑制,但是牺牲了响应速度,k1=8,k2=512,k3=0.1时,系统的超调量较小,响应速度也较小,动态性能较好。
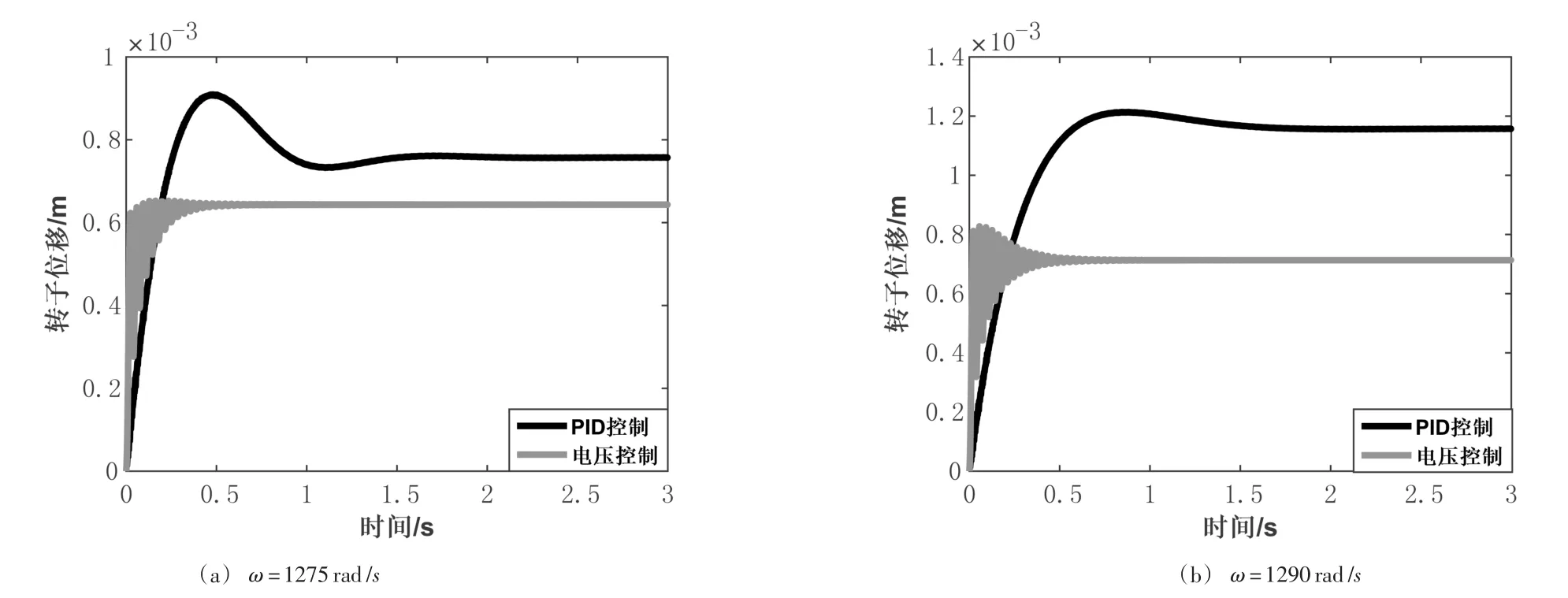
图4 两种控制方法下转子的时域响应对比Figure 4 Contrast of PID and voltage control when rotor pass through bending critical speed
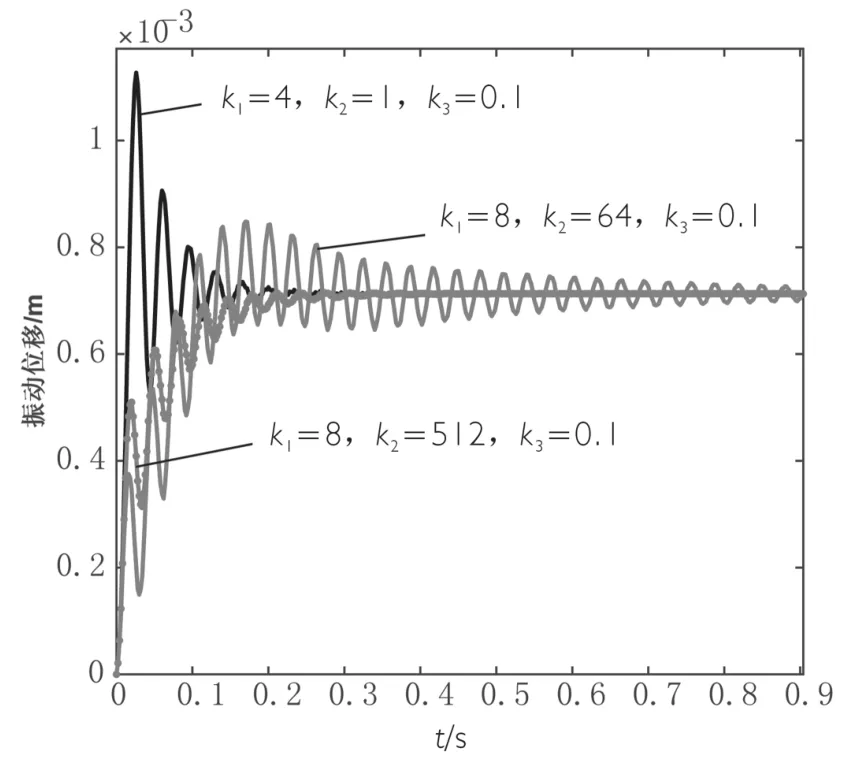
图5 不同控制参数下系统的动态响应Figure.5 Rotor’s dynamic response of different parameters
图6 展现了在不同能量修正参数k1下,电流校正系数k2对系统的超调量和响应时间的影响变化规律。总体上k1越大,系统的超调量越大,响应速度越快。从变化趋势来看,当k1=0.1时,超调量和响应时间都随着k2的增大而减小;当k1>1时,随着k2变大,超调量先减小,再增大,而响应速度一开始没有明显变化,当k2>100后,开始迅速变大。可以看出,当k1的值相差较大时,系统的动态性能随k2的变化规律会呈现相反的变化。根据仿真结果,当k1在1左右,k2在60~120左右时,系统动态性能较好。
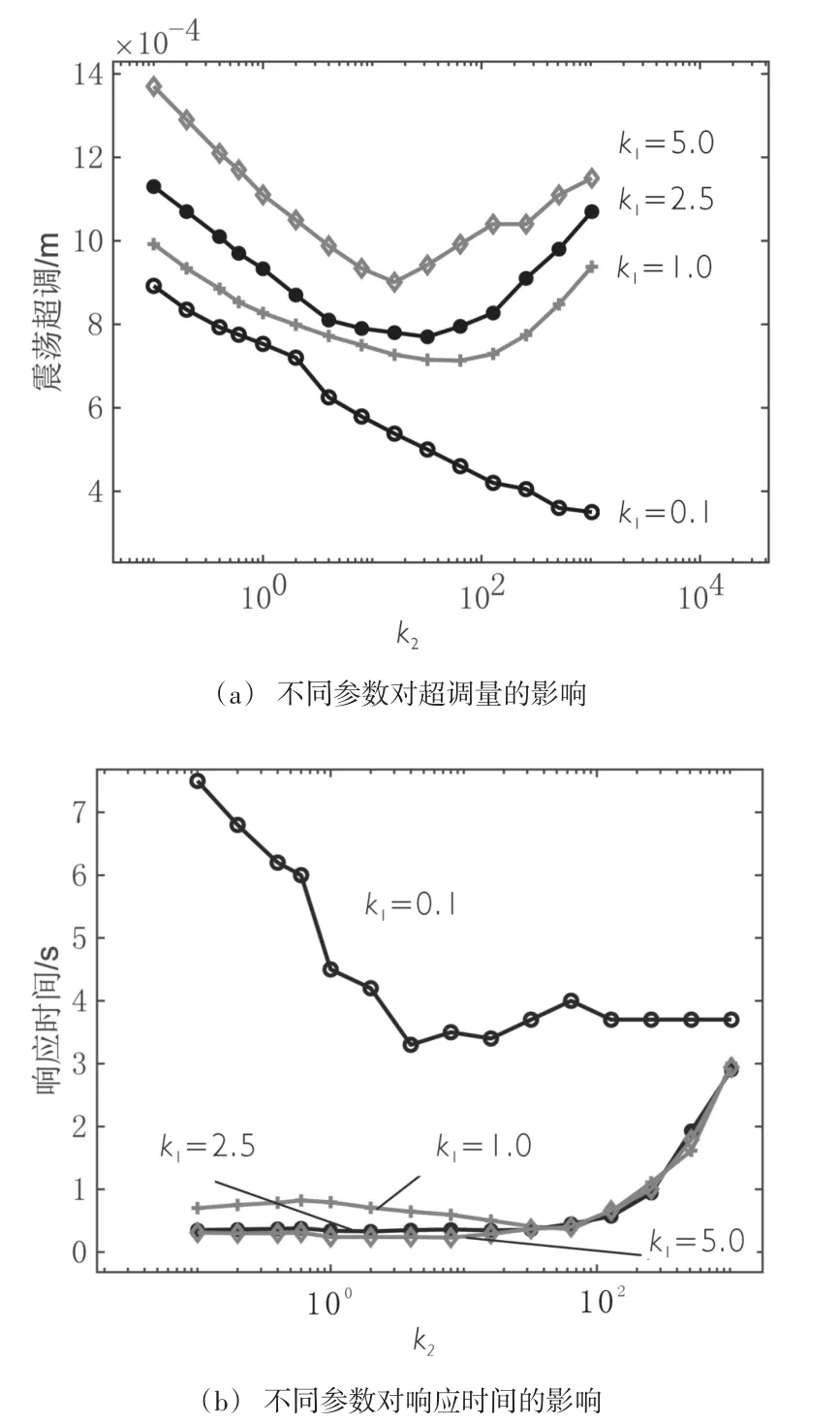
图6 不同k1下k2对系统动态性能的影响变化Figure.6 Rotor’s dynamic performance when k2varying in different k1
图7 展现了在不同电压放大倍数k3下,电流校正系数k2对系统的超调量和响应时间的影响变化规律。总体上k3越大,系统的超调量越小,但响应时间则随着k2变化产生不同的结果。从变化趋势来看,当k3≤0.1时,超调量随着k2增大先减小再增大;k3=0.4时,超调量随着k2增大而增大。另一方面,当k3<0.1时,响应时间随着k2的增大而增大;当k3≥0.1时,响应时间随着k2的增大先减小再增大。同样可以看出,不同的k3会使系统的动态性能随k2的变化规律更加复杂。从仿真结果来看,当k3在0.1左右,k2在60~100左右时,系统动态性能较好。
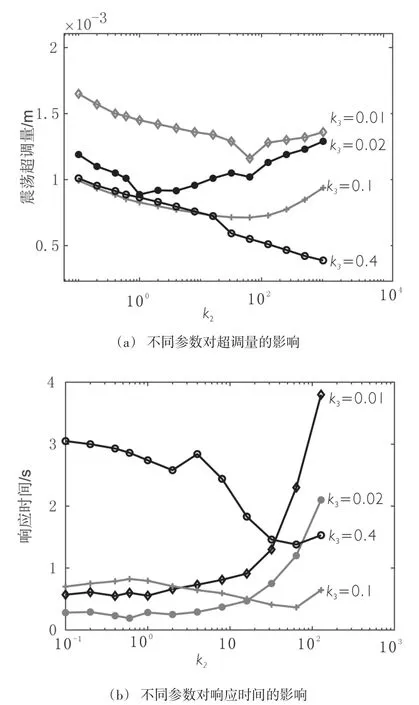
图7 不同k3下k2对系统动态性能的影响变化Figure.7 Rotor′s dynamic performance when k2varying in different k3
4 结论
针对电磁轴承中柔性转子跨越临界转速会产生较大振动的问题,设计基于系统能量的李雅普诺夫控制算法,并进行仿真验证。结果表明:
(1)在临界转速附近,基于能量的李雅普诺夫控制方法能够有效降低柔性转子的最大振动量,并提升了系统的响应速度,但是也牺牲了部分动态动态性能,使系统在上升过程中产生了一定程度的高频震荡。
(2)不同能量系数k1、电流修正系数k2和电压放大倍数k3下,电磁轴承的稳态性能没有差异,但是动态性能则产生了较大不同。根据仿真结果,随着k1、k3取值的变化,电磁轴承的动态性能会产生较大程度的变化,因此,需要选择合适的参数,从而得到良好的动态性性能。
