图像处理中拉普拉斯矩阵的稀疏化处理*

田俊杰，赵祖烨，张军飞

（1.华中科技大学材料成型与模具技术国家重点实验室，湖北武汉 430074；2.广州中望龙腾软件股份有限公司，广东广州 510000）

0 引言

图像处理和计算机图形学中有大量问题可以使用离散泊松方程来求解。图像处理领域的研究包括Levin等[1]提出的图像着色，Lischinski等[2]使用的色调调整，以及边缘保留平滑[3]和Xu等[4]提出的相对总变化量纹理剔除算法。泊松方程方法虽然在质量和数学简洁性方面表现出色，但其计算成本相当较大，需要求解非常大且不易求解的线性系统。

Matrix iterative analysis讲述矩阵迭代器运算的基本原理[5]，Iterative methods for sparse linear systems讲述求解稀疏线性系统的各种迭代器方法。对于常见图像处理领域算法中不均匀拉普拉斯矩阵求逆的加速有指导意义[6]。

许多图像处理算法实现过程中用到稀疏的不均匀拉普拉斯矩阵，当图案像素行列数分别为M和N时，保边滤波和图像着色等算法中的拉普拉斯矩阵的大小为MN×MN。算法求解过程需对拉普拉斯矩阵进行求逆，直接求逆的时间复杂度为O((MN)3)，在时间和内存上的消耗都是无法接受的。对于大型稀疏矩阵线性系统可以利用迭代法来加快求解，经典的迭代法有Jacobi迭代器方法，Gauss-Seidel迭代器方法，SOR迭代器方法等。本文作者主要应用不完全Cholesky分解与预处理共轭梯度法[6]，并将使用分层稀疏化对迭代器进行处理以减少时间和内存消耗。

D Krishnan等[7]为在计算机图形领域的算法中经常出现的离散泊松方程提出一个新的多级稀疏化方案。该方案根据邻域内粗细变量的拓扑关系选择不同的稀疏方法，时间复杂度高，且在分层稀疏化处理过程中无法抑制条件数的增长，本文作者采用一种更简单有效的稀疏化方法。

1 算法应用场景

Farbman等[3]提出加权最小二乘滤波算法(WLS)：

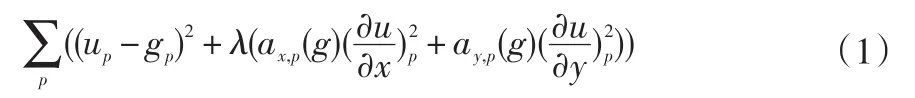
式中：g是输入图像，找出使式（1）有最小值的u即是想要的输出图像；p是像素点的索引；是在像素点p处的梯度；ax,p(u)表示权重大小。

原理是输出图像和输入图像的每个像素值尽量接近，且输出图像中的非边界区梯度尽量小。

式（1）可以转化为矩阵形式：

其中L为大型稀疏的拉普拉斯矩阵，稀疏矩阵求逆一般采用迭代法，但迭代法直接求逆会消耗大量时间。

文献[4]在WLS的基础上提出一种相对总变化量算子在保留图像边界的同时剔除纹理。纹理和主结构在相对总变化量算子上展现出完全不同的属性，由此可以在加权最小二乘法的过程中应用不同的权值对纹理和主结构进行不同程度的惩罚。文献[4]主要的公式是：

其中L也是一个大型稀疏的拉普拉斯矩阵。

2 算法分析

采用一种分层稀疏化的方案减少矩阵求逆的时间消耗。一个矩阵L关于向量x的能量函数由Rayleigh商定义:

由于L的半正定型，能量值总是非负数。矩阵L的特征向量对应的能量值是特征向量的对应的特征值，由Lx=λx得(xTLx)/(xTx)=(xTλx)/(xTx)=λ对称正定矩阵的条件数定义为：

迭代法通过一次次迭代来逐步逼近离散泊松方程的真实解，而所需的迭代次数与矩阵的条件数相关。Jacobi和Gauss-Seidel迭代法需O(κ)次，共轭梯度法需要O(κ)次[6]。所以加快迭代求解的方式之一就是减小矩阵的条件数。

关于减少矩阵条件数的途径，D Krishnan等[7]提到一种分层稀疏化方法，每层中都将节点划分为粗节点C和细节点F，通过迭代过程分层稀疏化矩阵。矩阵L可以划分为细节点C之间连接LCC，粗节点F之间连接LFF、细节点C与粗节点F之间连接LFC：

在L两边分别乘上得到原问题的一个更小规模的子问题。

根据粗细节点间的拓扑关系选择不同补偿方式稀疏化矩阵，采用一种更简单有效的矩阵稀疏化方式。采取去除局部三角形中最弱连接，补偿给其他两条边的方式来稀疏化矩阵以减少条件数，即将最弱边的权值加到相邻两边上，作为对去除最弱边的补偿。

图1 邻接三角形稀疏补偿示意图

分层稀疏化算法过程：

（1）对矩阵L中所有节点间的三角形，应用稀疏化和惩罚过程。得到结果矩阵L。

（3）迭代过程的停止条件是矩阵L中节点之间的连接数减少到规定值。由算法2的迭代过程可得到不同稀疏程度的矩阵P的一个集合[P1P2P3P4P5P6... Pn]和最终的稀疏矩阵L～；由这两者可用Krishnan等[8]中的算法1构成一个分层预处理器F(x)，在求解线性方程Lx=b时，用F(x)代替Lx，减少方程的条件数以加快方程求解。

3 结果分析

3.1 对条件数的影响

对图2应用中的纹理剔除算法，在式中L求逆时应用稀疏化处理。在矩阵迭代求逆过程中根据式（8）统计矩阵的条件数，图3所示是处理前和处理后迭代过程中条件数的变化。由图中信息可以看出，稀疏化处理可以减小条件数、加快迭代过程的收敛。

图2 图案样本

图3 分层稀疏化对矩阵条件数的影响

3.2 对处理时间的影响

收集500张如图2所示图片，从中提取出像素大小分别为64×64、256×256、1024×1024的图案，组成测试处理时间的样本库。CPU为i5-4460，3.2GZ四核处理器，软件运行环境是matlab2015a。以保边滤波的结果求解过程为例测试分层稀疏化对图像处理加速效果。即在式（3）中L求逆过程中，比较不应用稀疏化处理和应用稀疏化处理后迭代法解方程所需时间。

由表1中分层稀疏化前后平均求解时间的对比可以看出，对于像素行列数的图案，分层稀疏化算法对求解时间能产生的影响有限，随着图案像素行列数增加，分层稀疏化算法对求解时间的影响越来越大。

表1 矩阵求逆平均时间比较Tab.1 Matrix inverse average time comparison

4 结束语

本文作者提出一种对大型线性方程的系数矩阵进行预处理的方法。通过消去邻域三角形中权重最小的边、将权重补偿到其他两边并在子系统重复迭代该过程的方式构建分层预处理器。经大量实例验证，该算法对图像处理中应用广泛的泊松方程求解有着很好的加速效果，可以大大减小系数矩阵的条件数，减少时间消耗。