投资者情绪与股市收益率的非对称相关性分析

刘金娥,莫舒婷

(厦门理工学院经济与管理学院，福建 厦门 361024)

传统金融理论假定投资者完全理性，认为资产的价格只取决于基本面的因素，市场均衡时资产价格等于其内在价值。但是随着金融市场的发展，出现了越来越多无法用传统金融解释的现象，即金融异象。在现实的市场交易中，由于市场信息不对称效应的存在以及投资者本身主观方面等各种因素的影响，几乎不可能存在完全理性的人。对于我国的股票市场而言，市场起步晚，发展的时间历程短，市场中的投资者结构也相对不合理,总体而言,投资者的非理性程度与欧美等国家的成熟市场相比一般会更高。特别是股票市场的大部分中小投资者由于专业知识和投资技巧的掌握程度低以及信息来源渠道单一，在投资决策的过程中容易产生严重的心理和行为偏差。行为金融学打破了传统金融理论的假设，提出资产价格不仅来自于基本面，还受到投资者的行为和心理因素的影响，比如投资者情绪等。投资者情绪是投资者基于对资产未来现金流和投资风险的预期而形成的一种信念。众多学者的研究发现了投资者情绪对股市收益及波动的影响[1-6]。

ARCH模型能准确地模拟时间序列变量的波动性变化[7]，并在金融学的实证研究中得到广泛应用和拓展。GARCH模型称为广义ARCH模型，是ARCH模型的拓展，较好地描述了金融市场的杠杆效应和波动反馈效应，在刻画金融时序数据时具有独特的优势[8]。在此基础上Kroner等[9]构建了多元GJR-GARCH-BEKK 模型，分析了每个变量波动方程中的非对称效应以及两个变量波动间条件方差非对称性的溢出效应。本文进一步改进Kroner等[9]的方法，构建VAR-BVGJR-GARCH-BEKK模型，创新性地将非对称模型引入投资者情绪与股市收益率的研究，为宏观经济政策的制定和投资者理性决策提供参考。

一、VAR-BVGJR-GARCH-BEKK模型的构建

考虑到正负冲击的非对称性，构建VAR-BVGJR-GARCH-BEKK模型来分析投资者情绪与股市收益率之间的关系。首先构建VAR模型分析变量间均值溢出效应。然后基于正负冲击的非对称效应，根据VAR模型回归残差构建VAR-BVGJR-GARCH-BEKK模型，以检验变量间的波动溢出效应。

二元VAR-BVGJR-GARCH-BEKK模型的均值方程设定为

(1)

式(1)中：Rt是股市收益率;SENTt是投资者情绪指标;S=(s1s2)T为截距项；Φj为回归参数距阵;J是最佳的滞后阶数;εt=(ε1,tε2,t)T是残差向量;Ωt-1是截止到t-1期可获得的信息集。

二元VAR-BVGJR-GARCH-BEKK模型的方差-协方差方程设定为

(2)

式(2)中:C、A和G都是2×2阶参数矩阵，C为下三角常数矩阵，刻画条件方差方程的常数部分，A代表ARCH项的系数矩阵;G代表GARCH项的系数矩阵;D代表正负冲击引起的非对称影响的程度。具体表现为：

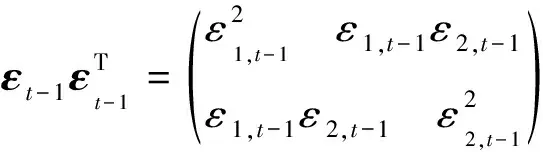
矩阵A主对角线元素aii(i=1,2)衡量变量自身波动的ARCH效应，即变量自身滞后的残差项平方对当期条件方差的影响程度，非主对角项元素aij(i,j=1,2;i≠j).衡量ARCH型波动溢出效应，即i变量滞后的残差项平方对当期j变量条件方差的影响程度。矩阵G主对角线元素gii(i=1,2)衡量变量自身波动的GARCH效应，即变量自身滞后的条件方差对当期条件方差的影响，非主对角项元素gij(i,j=1,2,i≠j)衡量GARCH 型波动溢出效应，即i变量滞后的条件方差对当期j变量条件方差的影响程度。矩阵D主对角线元素dii(i=1,2)衡量变量受到自身滞后的负冲击的非对称效应，非主对角项元素dij(i,j=1,2;i≠j)衡量j变量受到i变量滞后的负冲击的非对称效应。为此可做如下的假设检验。

假设1：变量1对变量2没有单向波动溢出效应，则a12=g12=d12=0。

假设2：变量2对变量1没有单向波动溢出效应，则a21=g21=d21=0。

假设3：变量1与变量2没有存在相互的波动溢出效应，则a12=g12=d12=a21=g21=d21=0。

除此之外，通过对非对称项系数D施加约束就可以单独检验是否存在正负冲击的非对称影响。为此做如下假设检验：

假设4：变量1滞后的负冲击向变量2没有单向的非对称性效应，即d12=0。

假设5：变量2滞后的负冲击向变量1没有单向的非对称性效应，即d21=0。

假设6：变量1和变量2不存在相互的非对称性效应，即d12=d21=0。

二、变量选取与检验

(一)投资者情绪指标

1.投资者情绪原始指标的选取

在投资者情绪的度量工作中，一般是用直接指标和间接指标两种方法把投资者情绪量化。直接指标来源于具体的投资者对于市场最直接的主观认知，可以很好的反映投资者最为真实的态度。间接指标是指市场交易中那些对于投资者情绪具有一定代表性或相关性的数据指标。据此可以客观地从侧面研究市场中投资者的行为和投资者情绪。但是，由于直接指标和间接指标基本上都是相互独立的单一变量，很容易受到其他外来因素的干扰而使数据效果不明显，并且一般的单一指标都难以全面准确地反映市场的真实情绪走向。所以，更多的学者们开始着重于通过研究单一指标的共性来建立复合指标。

在选取投资者情绪指标过程中，借鉴Baker等[10]1 655-1 658、文凤华等[11]的主成分分析方法，选用封闭式基金折价率(CEFD)、IPO数量(IPON)、IPO首日收益率(IPOR)、股票市场市盈率(PEM)、换手率(TURN)、市场月平均交易量(TV)、基金净赎回率(NFRR)和A股新增开户数(NAN)共8个代表性较高受到业内广泛认可的市场指标。考虑到投资者情绪变量本身会存在一定的领先与滞后效应[10]1 656，为此将8个指标的滞后一期也作为备选指标，8个指标的定义见表1。

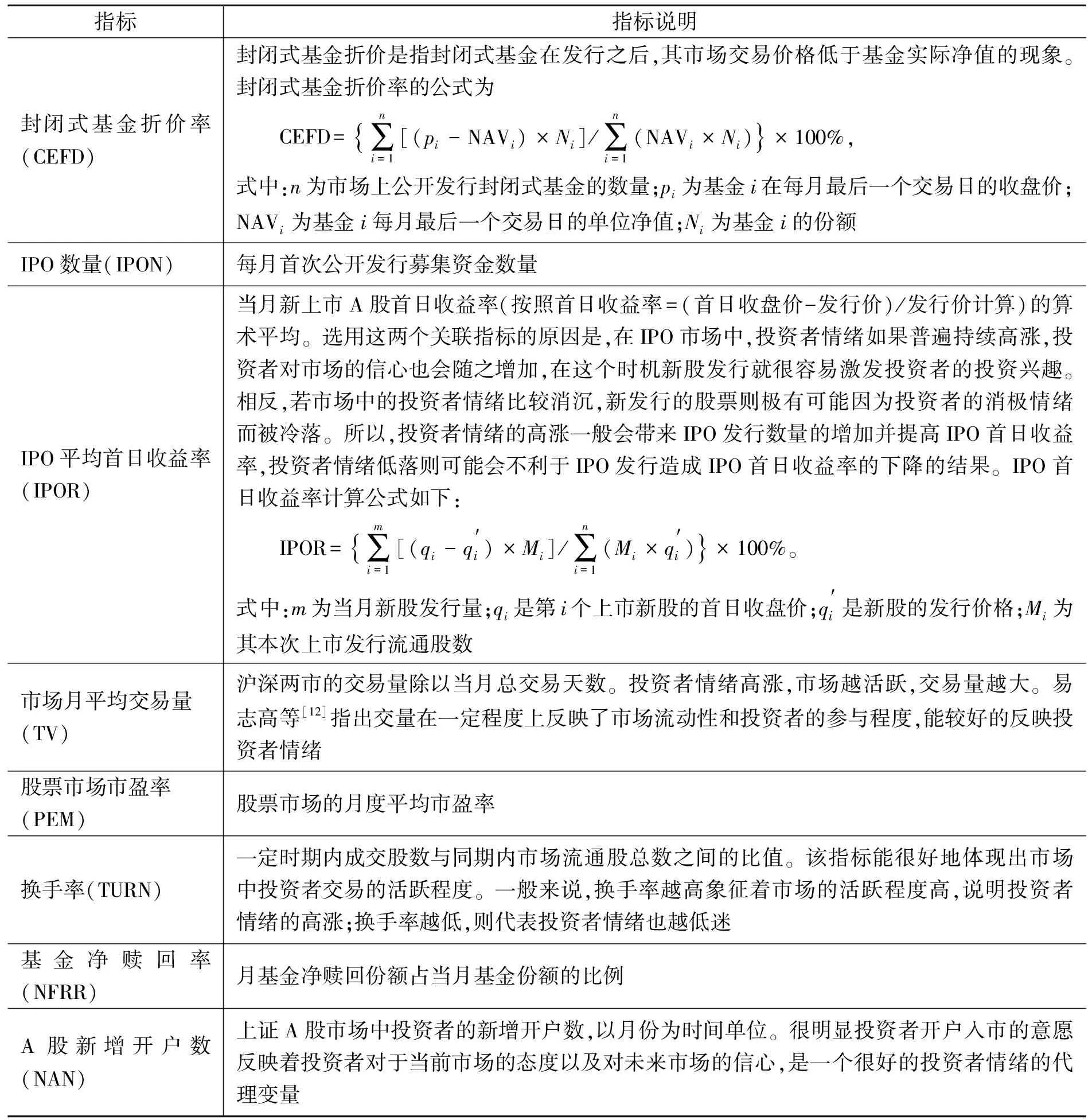
表1 单一情绪指标定义Table 1 Introduction of single emotion index

2.投资者情绪指标计算

所用数据均来自Wind数据库月度数据，所用股市收益率为上证综合指数收益率，样本期间为2003年1月—2016年6月。将表1中的8个指标及其滞后一期的8各指标，共16个变量进行主成分分析并加权平均，分别与投资者情绪指标(SENT)进行相关性分析，结果如表2所示。

表2 SENT与16个变量的相关性分析结果Table 2 Correlation coefficient between SENT and 16 variables

注：上标*、**、***分别表示在10%、5%和1%显著性水平下拒绝原假设；t和t-1分别表示当期和滞后一期变量。

通过表2的相关系数分析，最后选择CEFDt、PEMt、IPONt-1、IPORt-1、TURNt-1、TVt-1、NFRRt-1、NANt-1这8个相关系数最大的变量作为投资者情绪变量。

考虑到宏观经济因素的潜在影响，投资者情绪不仅受到自身心理因素的影响，还会受到宏观经济基本面的影响，因此引入居民消费价格指数、工业生产增加值以及宏观经济景气指数的一致性指数这3个指标作为控制变量，以剔除宏观经济基本因素对投资者情绪的影响。为此我们将所选取的投资者情绪的8个源指标分别对控制变量进行回归分析获得残差序列，再对残差序列进行主成分分析，得出前5个主成分的特征值累计贡献率高达89.32%，使用前5个主成分进行加权平均计算最终的投资者情绪指标(SENTt)，即

SENTt=0.229 8CEFDt+0.096 3PEMt+0.209 9IPONt-1+0.171 5IPORt-1+0.045 2TURNt-1+0.193 5TVt-1+0.147 7NFRRt-1+0.170 0NANt-1。

(3)

式(3)中，投资者情绪与CEFD、PEM、IPON、IPOR、TURN、TV、NFRR和NAN正相关。

(二)股市收益率及检验

实证分析设计股市收益和投资者情绪指标两个变量。投资者情绪指标由公式(3)可得。股票市场收益取以沪深300指数为基础计算的对数收益率(Rt),样本区间为2003年1月—2016年6月，投资者情绪指标与股市收益率走势如图 1所示。

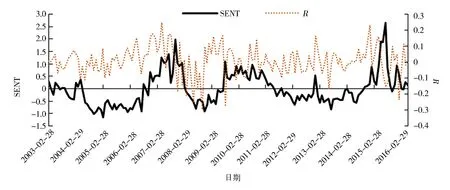
图 1 投资者情绪指标与股市收益率走势图Fig.1 Trend for investor sentiment and stock yield

当SENT大于0时，表示市场上的投资者情绪处于乐观积极的状态，而当SENT小于0，则表示市场上的投资者情绪处于消极悲观的情绪状态。从图1可以看出，SENT与Rt在趋势上大体一致，两个变量之间存在较高的相关性。在SENT大于0时，市场收益率也跟随着往上升，在证券市场上，投资者的“追涨杀跌”行为特征，使得投资者在牛市中受市场上扬趋势的影响，容易出现积极乐观的投资者情绪。投资者情绪指标SENT小于0的时间段里，市场收益率基本处于该时期里一个相对的低水平位置，在证券市场上，熊市中受市场下跌趋势的影响就容易出现消极悲观的投资者情绪。2006年下半年至2007年与2014年下半年至2015年的上半年投资者情绪明显偏高，而2004年至2006年上半年、2008年与2011年至2014年上半年投资者情绪明显偏低。

值得注意的是，在图1中2015年4月—6月的时间段里，此时投资者情绪指标处于一个最高点，但实际上同一时期的股市却是意外大跌，市场收益率也是一个走低的趋势。如果单从投资者情绪的角度考虑的话，可以猜测，当投资者情绪水平过高甚至达到了一定的上限时，说明市场上投资者看待市场的理性态度在减少，从而使市场收益率反而走低。另外，消极的投资者情绪充斥市场并不代表市场收益率必定是绝对性的降低。如2014年3月的投资者情绪位于一个最低点，但相应的市场收益率却比较高。在国内外的研究中，不少学者已经发现在股票市场中，投资者的积极情绪和消极情绪对股票价格行为的影响是非对称的。也就是说积极的投资者情绪和消极的投资者情绪各自对股票市场的影响并不存在等量的影响力。在这一问题上，文凤华等[11]的理论解释是，在投资者情绪处于一定程度的低水平时，由于市场上非理性投资者属于投资者情绪敏感的群体，容易受心理因素的影响而对市场失去信心，参与投资市场的积极性下降，从而纷纷退出市场。这时，理性人占据市场投资者的比例就会大大提高，甚至最终可能在市场中起主导作用，形成一个相对有效的市场。所以，当投资者情绪位于一定程度的低位时，很有可能恰好就是收益率走高的时机。

表3是变量描述性统计与单位根检验结果。标准差表明投资者情绪的波动幅度大于股市收益率;偏度和J-B统计量均表明两个变量并不服从正态分布，峰度值均大于3，表明市场对数收益率和情绪变量都呈尖峰厚尾分布特征;Q统计量表明两变量均具有一定程度的自相关;ADF检验表明两变量均是平稳系列。

表3 变量描述性统计与单位根检验Table 3 Descriptive statistics and unit root tests for the variables

三、投资者情绪与股市效益的相关性

根据构建的VAR-BVGJR-GARCH-BEKK模型分别对变量间的均值溢出效应和波动溢出效应进行检验，以分析投资者情绪与股市收益率的相关性。

(一)均值溢出效应

首先根据VAR模型的滞后阶数选择准则LogL、LR、FPE、AIC、SC和HQ综合确定VAR模型的滞后阶数，可以发现在最大滞后阶数是12阶的情况下，LR、FPE、AIC选择准则认为应该建立最优滞后阶数是6，SC选择准则认为最优滞后阶数是1，HQ选择准则认为最优滞后阶数是2，因此确定VAR模型选择VAR(6)。

从VAR模型的特征根情况可以发现，VAR模型特征根均落在单位圆内，所以所确定的VAR(6)模型是稳定的。对VAR(6)模型所进行的white检验，结果说明残差序列存在显著的异方差特性，因此将进一步采用VAR-BVGJR-GARCH-BEKK模型来研究两变量间的溢出效应。

基于VAR-BVGJR-GARCH-BEKK模型的均值方程的回归结果(见表4),检验股市收益率与投资者情绪之间的均值溢出效应。

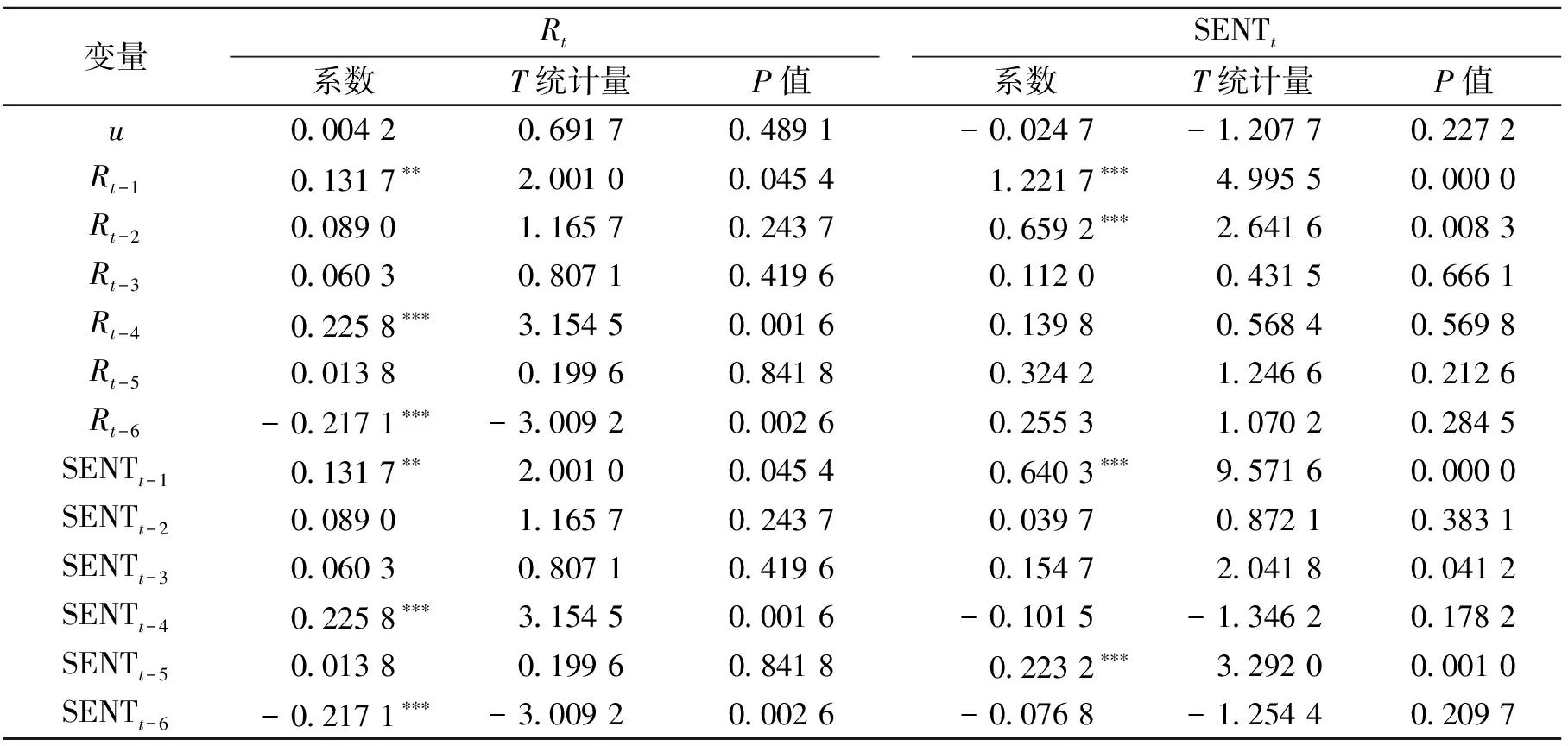
表4 VAR-BVGJR-GARCH-BEKK模型的均值方程回归结果

注：*、**、***分别表示在10%、5%和1%显著性水平下拒绝原假设。

由表4知两变量的滞后项均对其各自当期值具有显著的影响，说明两变量均存在系列自相关，与表2的结果一致。在股市收益率方程中，滞后2期、6期的投资者情绪的回归系数显著不为0，说明投资者情绪会影响股票市场行情，从而影响股市收益率。在投资者情绪方程中，滞后1期、2期和6期的股市收益率的回归系数显著不为0，说明股市收益率会对投资者情绪产生影响。综上，股市收益率与投资者情绪存在双向的均值溢出效应。

(二)波动溢出效应

基于VAR-BVGJR-GARCH-BEKK模型方差回归结果见表5。

表5 VAR-BVGJR-GARCH-BEKK模型的方差方程回归结果Table 5 Variance equation regression results of VAR-BVGJR-GARCH-BEKK model

注：*、**、***分别表示在10%、5%和1%显著性水平下拒绝原假设。

从股市收益率看，a11、g11分别在1%水平和10%水平下显著，这表明股市收益率滞后的扰动会加大当期的波动，d11<0即具有聚集性。说明股市收益率的正面冲击会减少股市收益率的波动，这与国际上发达国家的股市特征一致，但d11在统计意义上不显著，在一定程度上说明我国的股票市场还不是很成熟。

从投资者情绪看，a22、g22均在1%水平显著，表明投资者情绪滞后的扰动会加大当期的波动，即波动聚集性明显。d22≥0且在1%的水平下显著,表明投资者情绪的波动对于自身滞后的负冲击具有非对称效应，投资者情绪的负面冲击会显著加大投资者情绪的波动，即投资者情绪受到自身滞后的负冲击比受到自身滞后的正冲击产生更大的波动。这符合行为金融学中的“损失厌恶”，即损失带给一个人的痛苦，要大于收益带给一个人的喜悦。

为了说明股市收益率与投资者情绪间的波动溢出效应情况，进行Wald检验(结果见表6)，从检验结果发现股市收益率与投资者情绪间存在显著的双向波动溢出效应，任何一个变量的波动信息都会传递到另外一个变量中，对另一变量的波动产生影响。

表6 VAR-BVGJR-GARCH-BEKK模型检验Table 6 Test analysis of VAR-BVGJR-GARCH-BEKK model

通过非对称性检验发现，股市收益率与投资者情绪之间的波动溢出效应具有显著的非对称性。非对称矩阵系数d12<0但不显著，说明在统计意义上股市收益率的冲击对投资者情绪的影响不存在非对称性；d21>0且显著，说明投资者情绪的冲击对股票市场收益的影响具有非对称性，投资者情绪的正面冲击会加大股市收益率的波动，即当投资者情绪高涨时预期市场收益的波动性会加剧，投资者情绪低落时预期市场收益的波动性会减少。

四、结论与政策建议

选取2003年1月—2016年6月上证综合指数和适合我国市场情况的8个反映投资者情绪的指标月度数据，构建VAR-BVGJR-GARCH-BEKK模型，然后通过模型分析了股市收益率与投资者情绪之间的相关性，研究发现股市收益率与投资者情绪之间存在相互影响。第一，投资者情绪与股市收益率存在双向的均值溢出效应，任何一个变量的变动都会影响另一个变量；第二，股市收益率与投资者情绪间存在显著的双向波动溢出效应，任何一个变量的波动信息都会传递到另外一个变量中，对另一变量的波动产生影响；第三，投资者情绪受到自身滞后的负冲击比受到自身滞后的正冲击产生更大的波动，投资者具有“损失厌恶”的特征；第四，投资者情绪的正面冲击会加大股市收益率的波动，当投资者情绪高涨时预期市场收益的波动性会加剧，投资者情绪低落时预期市场收益的波动性会减少。

我国属于新兴市场国家，相比国外成熟的市场国家投资者的非理性程度更高，且目前我国证券市场个人投资者仍然占据较高比例。基于此，首先，监管部门应积极培育并引导机构投资者进入证券市场，发挥机构投资者的知识优势和信息优势，减少投资者的非理性行为偏差，以减少其情绪的大幅度波动；其次，应关注投资者情绪与股票市场收益两者之间的关系，引导投资者做出更为理性的分析和判断，避免投资者非理性产生的“追涨杀跌”行为；再者，应该强化信息披露的规范性和及时性，提高市场的有效性，这有利于投资者合理预期的形成，减少投资者的非理性预期的形成，进而减少投资者情绪的波动，有助于证券市场的健康持续发展。