人-结构体系的竖向动力响应试验研究
2018-10-09贺梦悦张芝芳徐梅玲
贺梦悦,张芝芳,徐梅玲
(1.广州大学 淡江大学工程结构灾害与控制联合研究中心,广东 广州 510006;2湖北正天工程咨询有限公司,湖北 宜昌 443000)
近年来,公共建筑结构(体育场、火车站和人行桥等)因其材料力学性能的不断优化,逐渐向轻质轻柔、大跨度和不规则的趋势方向发展,使结构的固有频率越来越低,当落入人行荷载的频带范围时极易产生共振现象,导致一系列突发事件[1-2]。如英国伦敦的千禧桥由于观光人潮过多导致桥面共振摇摆被迫封桥,后经安装90个避震器才得以开放。由此可见,研究人群荷载与结构的相互作用机理显得十分重要。
人体作为复杂的生物弹性系统,包含众多不同共振频率的组织和器官,建立人体模型十分困难。Lenzen[3]发现人群作用使得体系的共振频率低于原固有频率,因此将人群整体模拟为附加质量块作用于结构。然而这并不能完全反映人群对结构的影响;1975年Polensek[4]及1981年Rainer和Pernia[5]发现当人-结构体系除频率降低外,阻尼比在显著增大,该成果大大推动了人群荷载对结构影响的研究进展。学者们据此建立不同自由度的体系模型,并通过人-结构试验进行验证,目前主要集中在竖向作用的研究。Salyards[6]和Sim[7]对人体以不同姿势(跳跃、摇摆等)作用于悬臂结构时的影响情况进行分析;Ellis和Ji[8]对人体在楼板结构上有规律运动(舞蹈、有氧运动等)后的响应分析,得出描述人体荷载的模型,在对Twickenham露天体育场馆看台做动力反应测试时发现,体系出现了额外的共振频率,且分别低于和高于原结构的固有频率[9],说明人群应作为弹性体系附加于结构,而非简单等效为附加质量;孙惠芳[10]采用实测地铁车站数据,对不同个体(不同性别、年龄、身高、负重结伴和穿高跟鞋等)的步频进行了交通微观特性研究;姜伟等[11]人研究了居民长距离出行的交通选择;倪鹏炯等[12]人针对地铁突发事件,对体系的脆弱性进行了模糊综合评价研究;高世桥[13]等人对木质横梁测试后发现人体竖直和拍手站立于横梁跨中时,体系的固有频率均发生下降,而人体在竖直比活动时体系的阻尼比增加更大。
由于国内对人-结构体系的试验研究较少,基础性的数据相对较欠缺,因此本文将搭建“钢板-弹簧”单自由度平台模型,通过采用丹麦B&K公司PULSE振动机声学信号采集分析系统,对3种人体姿势工况下的人-结构体系竖向振动特性进行试验研究,进而验证人-结构体系的不同自由度理论模型,使人-结构体系间的相互作用研究进一步深入。
1 平台结构模型

图1 圆盘钢板


图2 弹簧

图3 模型2A-2
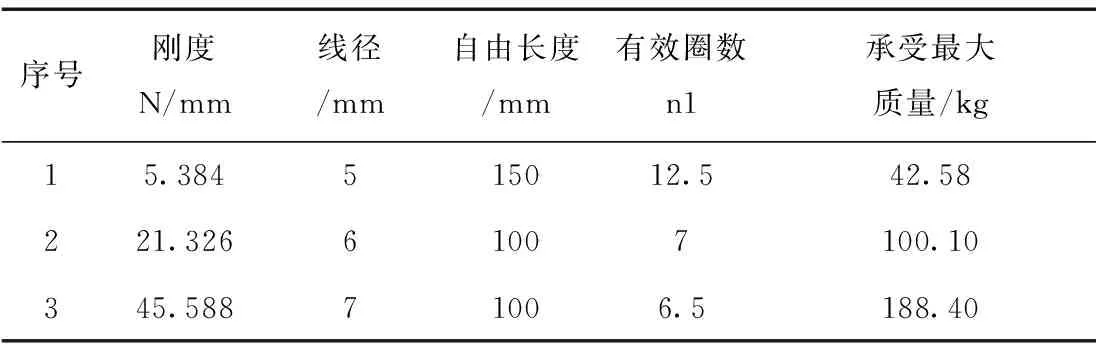
序号 刚度 N/mm 线径 /mm 自由长度/mm 有效圈数n1 承受最大质量/kg 1 5.384 5 150 12.5 42.58 2 21.326 6 100 7 100.10 3 45.588 7 100 6.5 188.40
2 测试过程
试验采用丹麦B&K公司PULSE振动及声学信号采集分析系统,获取测试模型的加速度时程图,利用软件自带的快速傅立叶变换(FFT)获得加速度功率谱图,从而确定人-结构体系的共振频率值。图4给出了结构平台模型(钢板)表面布置的加速度拾振B&K4381及测点布置图。其中1号拾振器采集竖直方向信号,2号和3号拾振器用于检测是否为竖直方向,当3个测点采集的功率谱中共振点对应的横轴(频率)为同一值时,该组数据合理。

图4 加速度拾振器(B&K4381)及测点布置图
图5展示了测试的3种工况,分别为单人竖直站立A盘,单人弯膝站立B盘,两人竖直站立B盘。试验参与者有15人(12男3女),体重范围在40~80 kg。通过橡胶锤有规律地敲击平台,并使模型振动的记录时长控制在30 s,每人每工况测试3次,志愿者须保证双脚位置不变,当至少有2组结果相同时作为该体系的共振频率值。为更真实地模拟实际平台结构,将不同的圆盘和弹簧组合得到以下单自由度模型,分别为A-2、A-3、2A-2、2A-3、3A-2、3A-3、B-2、B-3、A-B-2和A-B-3。

图5 人-结构体系测试工况
3 结果与分析
3.1 模型验证
考虑到人体质量相对于大跨结构的质量较小,且实际工程中常将结构简化为单自由度模型,故本文将结构平台作为单自由度模型,如图6所示。
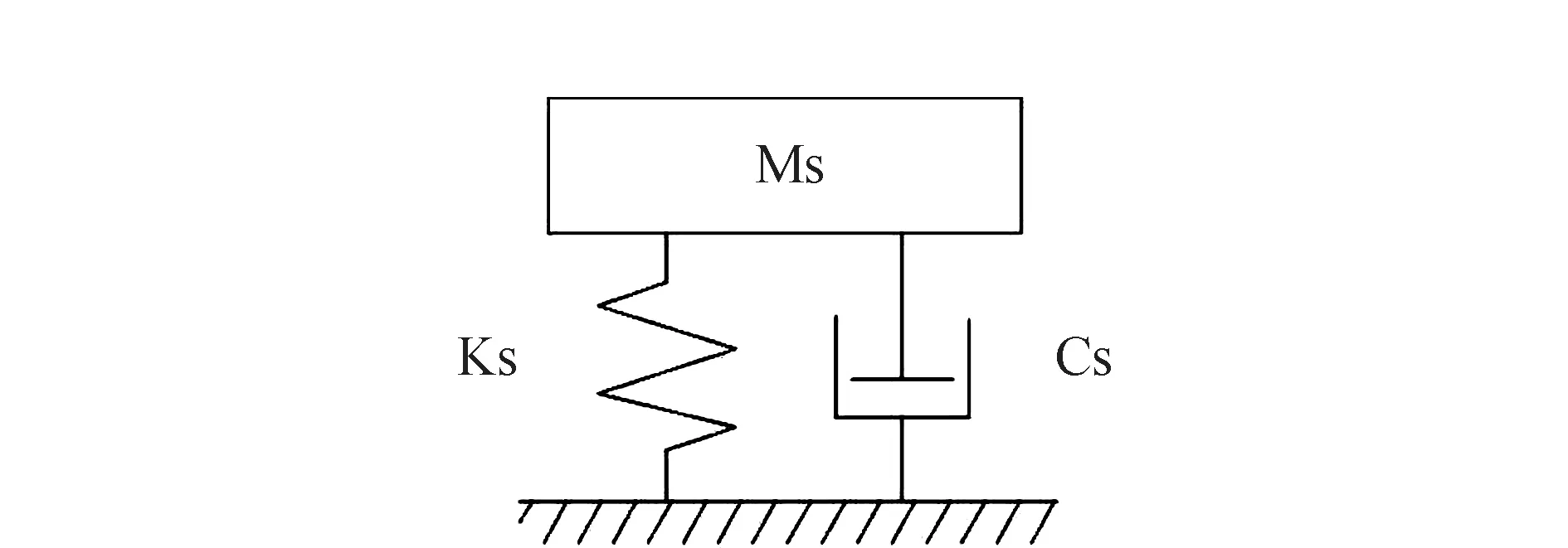
图6 结构单自由度模型
根据结构动力学[14]单自由模型的固有频率计算式(1),计算模型的理论固有频率。再由式(2)得到试验测试的模型频率与理论模型的固有频率的误差。
(1)
式中:k为单自由度的模态刚度,N/m;m为单自由度的模态质量,kg;f为单自由度频率,Hz。
U=(fexp-ftho)/ftho
(2)
式中:U为试验测试的模型频率与理论模型的固有频率误差,Hz;fexp为试验测试的模型频率,Hz;ftho为理论模型的固有频率,Hz。表2所示为不同组合下的理论固有频率与测试频率的对比结果。

表2 理论固有频率与测试频率对比
由表2可知理论固有频率与测试频率的误差均小于2.7%,证实了圆形钢板-弹簧模型能够较好地模拟单自由度模型。
3.2 加速度时程图分析
对模型B-3进行试验,得到加速度响应时程图和经快速傅立叶变换后的功率谱图。图7(a)—图7(d)分别对应空载和3种工况下被提取和放大后的加速度时程图。
从图7可以看出,人-结构体系加速度时程图的振动衰减时间均明显短于空载作用时间,故得出人-结构体系的阻尼比大于原结构本身的结论。同样地,对比观察图7(b)—图7(d)的振动时间长短,发现两人竖直站立、单人竖直站立和单人弯膝站立3种工况的振动衰减时间依次减小,意味着阻尼比依次增大。
3.3 共振频率分析
将加速度时程通过快速傅立叶变换(FFT)得到功率谱图,从而确定人-结构体系的共振频率值。图8展示了单人竖直站立于模型2A-2时的体系共振频率值,结构的固有频率(横线)均为8 Hz,其中图8(a)和图8(b)的横坐标分别为参与者身高递增和质量递增。根据式(1)可知当人体简化为附加质量块时,人-结构体系的共振频率必然小于结构固有频率。而试验结果出现了2个共振频率,一个高于原模型频率,一个低于原模型频率,该结论与Eills和Ji的发现一致[8],说明在轻柔结构中无法将人体简单定义为附加质量块,应将其作为弹性体附加于结构。

(a) 空载作用
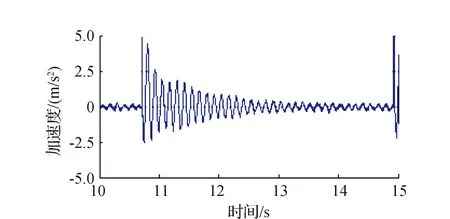
(b) 单人弯膝站立
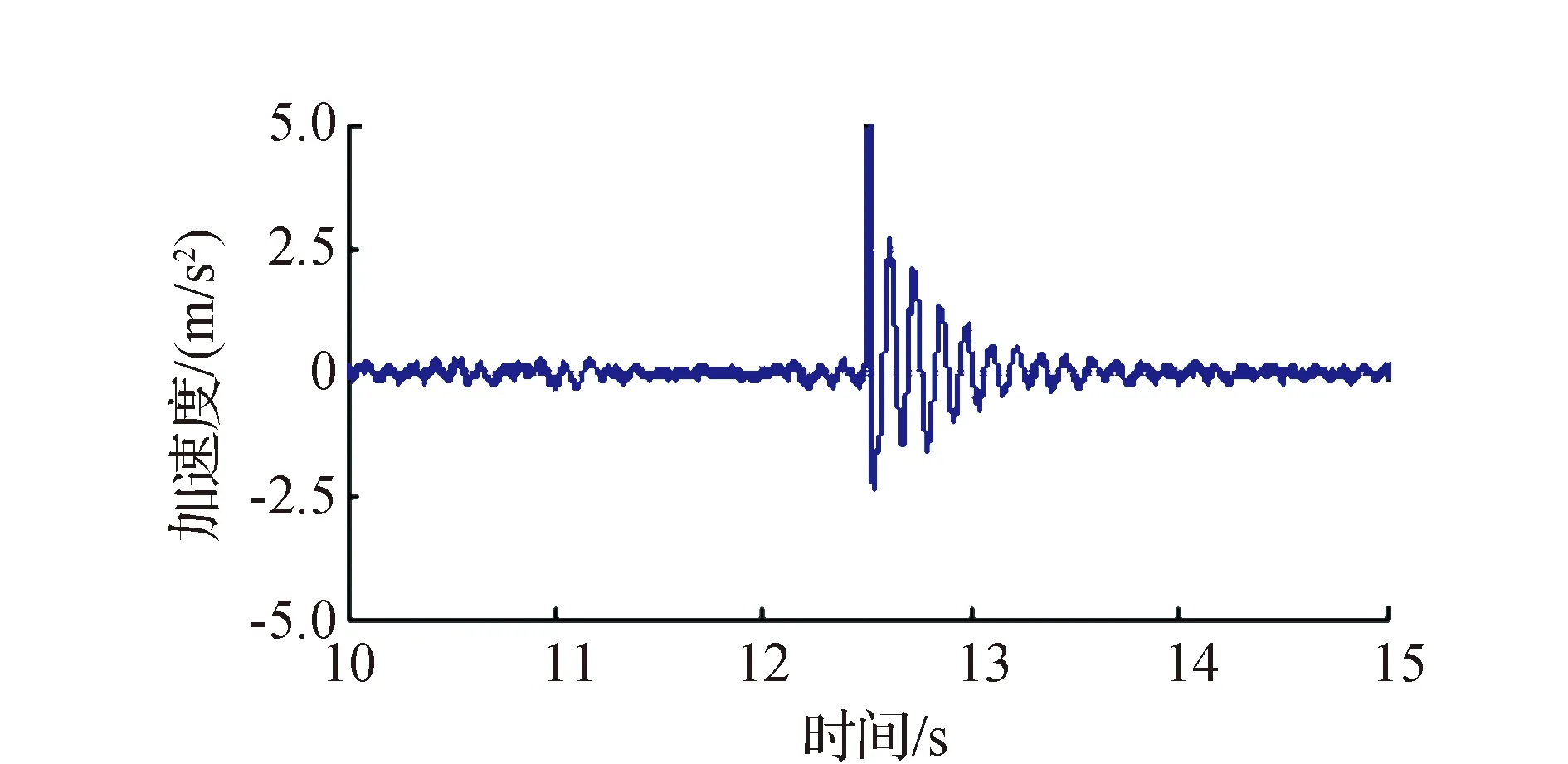
(c) 单人竖直站立
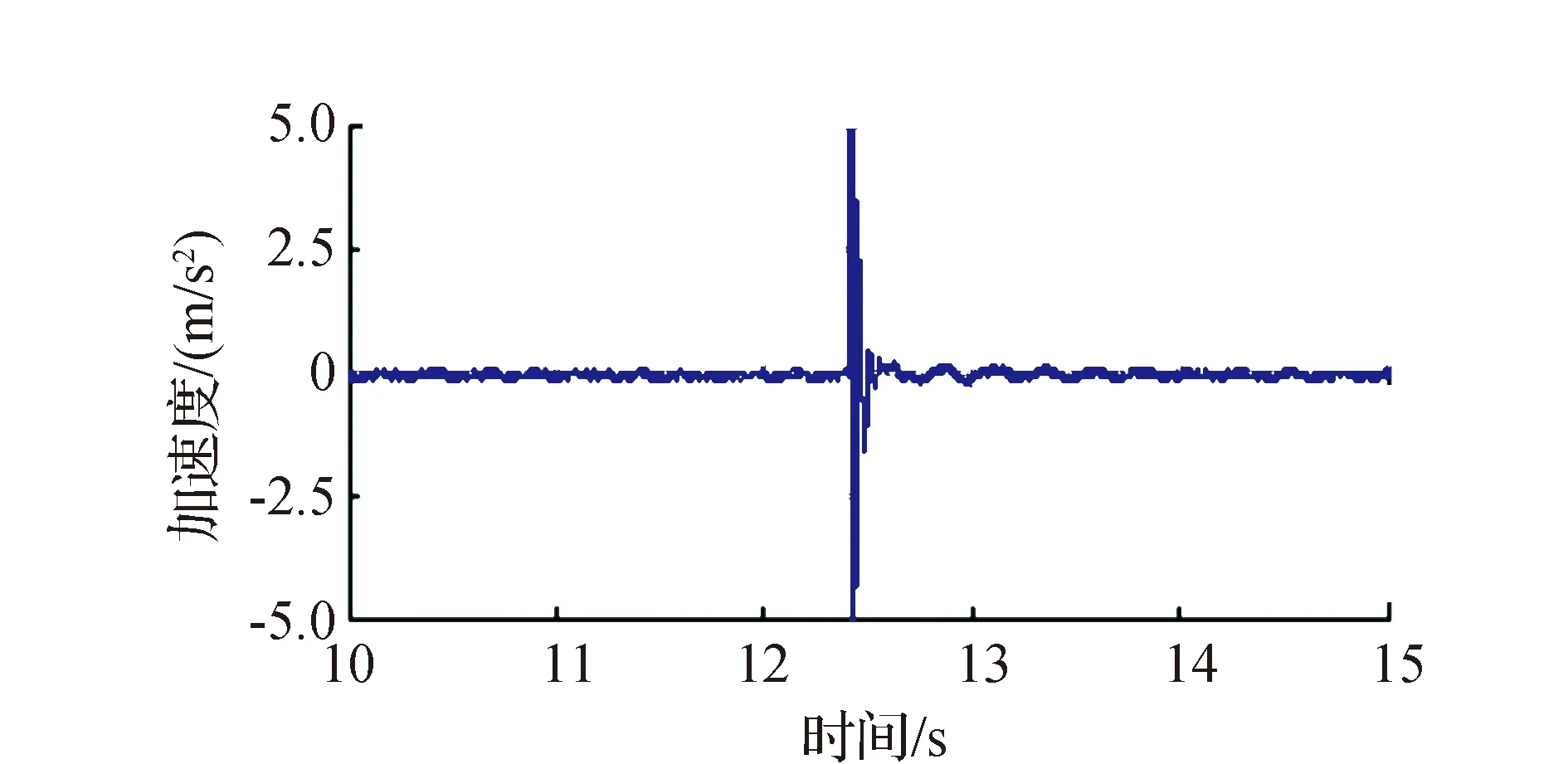
(d) 两人竖直站立图7 模型B-3的加速度时程图

(a)参与者身高递增

(b)参与者质量递增 图8 单人竖直站立于模型2A-2的体系共振频率
为研究单人在不同姿势(竖直站立、弯膝站立)作用下是否带来体系共振频率的变化,以模型B-3为例,如图9所示。发现当人以不同姿势站立于结构模型时,对人-结构体系的动力特性影响不同,故当人体被简化为质量-弹簧-阻尼模型时,需要依据人体的不同姿势调整各部分的参数。

图9 单人作用于模型B-3的体系共振频率
为研究相同结构固有频率(基频)和人体作用下的不同模型尺寸和形态对体系共振频率的影响,以模型3A-2和B-2为例(基频均为6.5 Hz),模型质量和弹簧型号均相同。图10展示了人体竖直站立于模型3A-2(方形)和模型B-2(三角形)时的人-结构体系共振频率值,发现当模型固有频率和参与者相同时,结构模型的尺寸和形态同样会影响人-结构体系的动力特性。
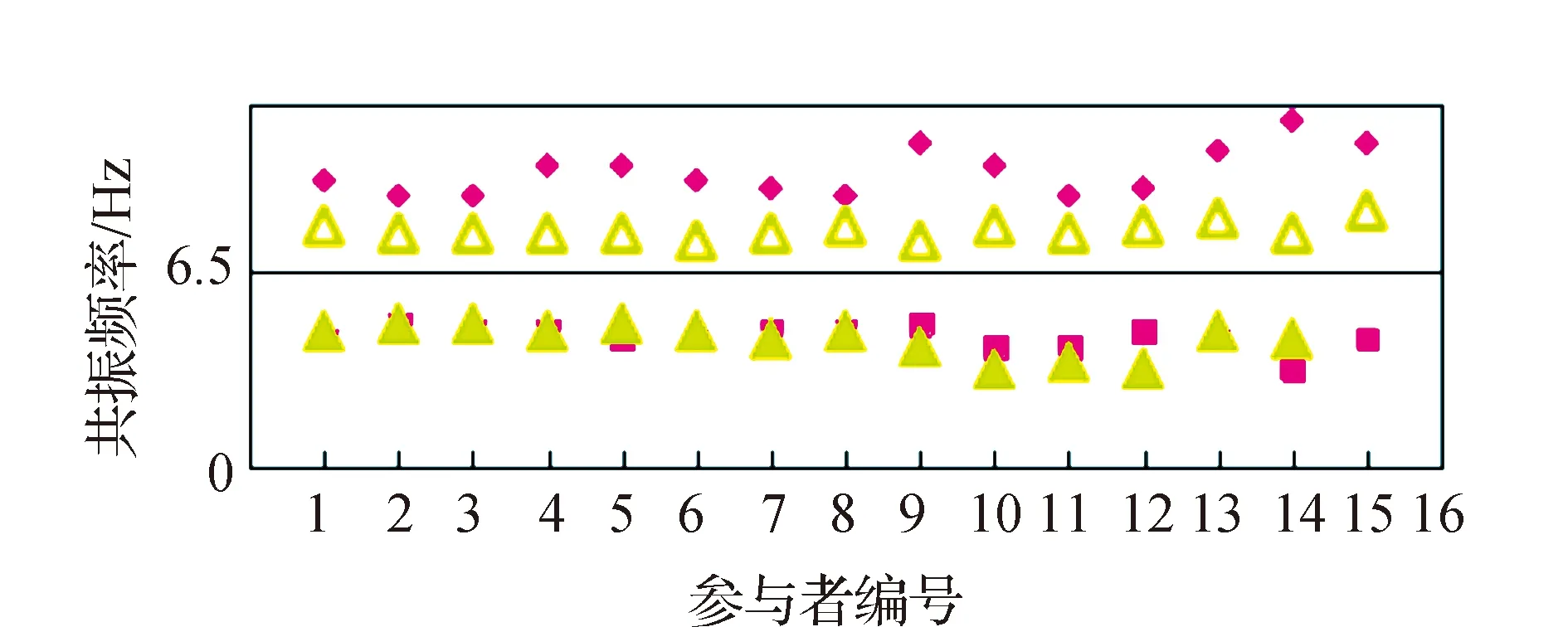
图10 人-结构体系共振频率(模型基频6.5 Hz)
4 结 论
本文通过搭建“钢板-弹簧”结构平台模型,对人体在不同姿势工况下的人-结构体系竖向动力响应进行研究,并获得基础性的试验数据。该研究成果验证了人-结构体系的不同自由度理论模型,进而得到人体模型参数,使得人群荷载与大跨结构体系之间的相互作用理论更充实。文章对比分析试验结果得到以下结论:
1) 当人作用于结构时,人-结构体系的阻尼比大于原结构本身,且竖直站立比弯膝站立时的阻尼比大;当竖直站立的人数增多,阻尼比变大。
2) 人-结构体系的共振频率出现一个高于原模型频率,一个低于原模型频率现象,说明轻柔结构中无法将人体简单定义为附加质量块,应将其作为弹性体附加于结构。
3) 当人以不同姿势(竖直、弯膝)站立于结构模型时,对人-结构体系的动力特性影响不同,故当人体被简化为质量-弹簧-阻尼模型时,需要依据人体的不同姿势调整各部分的参数。
4) 当模型固有频率和参与者相同时,测得的人-结构体系的共振频率不同,可知体系动力特性的因素不仅与模型频率、参与者有关,还包括结构简化模型的尺寸和形态等。
此外,本文仍存在不足之处,仅研究了人体对结构的竖向作用,以后可以拓展到人群作用及水平特性研究,还可尝试更复杂的结构模型和更多的人体姿势工况,如单脚站立、端坐和左右摇摆等的研究。
